Download Lecture 33 – Active Microwave Circuits: Two

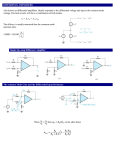
Whites, EE 481/581
Lecture 33
Page 1 of 11
Lecture 33 – Active Microwave Circuits:
Two-Port Power Gains.
We are going to focus on active microwave circuits for the
remainder of the semester. There are many types of active
circuits such as amplifiers, oscillators, and mixers. We will
concentrate only on amplifiers.
It is often a much more involved process to design and construct
active circuits that operate correctly than passive ones. Reasons
for this include:
 A bias network is required,
 The devices are nonlinear,
 Unintended oscillations produced by circuit instability.
More care, patience, and experience are often required in the
design of active RF and microwave circuits than purely passive
ones.
The analysis of such circuits is usually very difficult given the
nonlinear behavior of the devices. For linear amplifiers, though,
a linear analysis is applicable, which helps simplify matters.
For this reason, we will focus on linear, small signal amplifiers.
Furthermore, we will use measured (or given) S parameters for
the devices (transistors) rather than detailed device parameters
(β, C, r, etc.). Consequently, we can treat the transistor as a
© 2015 Keith W. Whites
Whites, EE 481/581
Lecture 33
Page 2 of 11
two port, but possibly one with gain. This approach works well
for the steady state analysis of linear, small-signal amplifiers.
For other types of active circuits, such as oscillators, mixers, or
power amplifiers, the nonlinear behavior of the circuit devices
must be explicitly accounted for, which precludes the use of S
parameters. Much more difficult.
One big difference with active devices is that the magnitude of
the S parameters may be greater than one. Often it is only S21
that has this characteristic, with port 1 serving as the input and
port 2 the output. With passive devices, S parameters with
magnitudes greater than unity are physically impossible.
Types of Power Gains
Referring to a generic two-port network circuit such as
Pin
PL
Z0
Z0
there are three commonly used definitions for power gain.
P
G L
1. Operating Power Gain:
Pin
(1)
Whites, EE 481/581
Lecture 33
Page 3 of 11
This is the ratio of the time-average power dissipated in a load
to the time-average power delivered to the network.
P
GA  av ,n
2. Available Gain:
(2)
Pav , S
This is the ratio of the maximally available time-average
power from the network to the maximally available timeaverage power from the source.
P
GT  L
3. Transducer Gain:
(3)
Pav , S
This is the ratio of the time-average power dissipated in the
load to the maximally available time-average power from the
source.
It is this latter transducer gain that you used in EE 322
Electronics II – Wireless Communication Electronics to
characterize the performance (i.e. gain) of the active devices in
circuits.
Among other applications, these three definitions of power gain
are used to design different types of amplifiers:
1. Operating Power Gain, G. Maximum linear output power
amplifiers.
2. Available Power Gain, GA. Low Noise Amplifiers (LNAs).
Whites, EE 481/581
Lecture 33
Page 4 of 11
3. Transducer Power Gain, GT. Simultaneously conjugate
matched input and output ports (leads to maximum linear
gain).
Power Gain Expressions
We will now derive analytical expressions for these power gains
in terms of the S parameters of the network, as well as the source
and load impedances. These will prove central to the design of
linear microwave amplifiers.
Referring to this generic two-port circuit (Fig. 12.1):
V1
ZS
VS
+
-
+
V1  S in
Z in
V1
V2
t1
[S]
(wrt Z0)
t2
 out  L
V2
TLs are infinitesimally short, with
characteristic impedance Z0.
ZL
Z out
then by the definition of the S parameters we can write
V1  S11V1  S12 LV2
(12.2a),(4)
and
V2  S 21V1  S 22 LV2
(12.2b),(5)
In these equations we have used the relationship V2   LV2 .
As we showed in Lecture 21 using signal flow graphs
Whites, EE 481/581
Lecture 33
V1
 S S
in    S11  L 12 21
1   L S 22
V1
Similarly, it can be show that
 S S
V2
 out    S 22  S 12 21
1   S S11
V2
Page 5 of 11
(12.3a),(6)
(12.3b),(7)
Next, by voltage division at the source and for an infinitesimally
short TL
Z in
V1 
VS  V1  V1  V1 1  in 
(8)
Z in  Z S
Z in
VS
V1 
so that
(9)
Z in  Z S 1   in
Now, using in   Z in  Z 0   Z in  Z 0  and after some algebra,
(9) can be reduced to
1   S VS
V1 

(12.4),(10)
1   S in 2
There are four different time-average power quantities we need
to determine in order to compute (1)-(3):
1. Pin: Time-average power provided by the source
| V1 |2
Pin 
1 | in |2 

2Z 0
Substituting for V1 from (10) gives
(12.5),(11)
Whites, EE 481/581
Lecture 33
| VS |2 |1   S |2
2
1
|
|
Pin 




in
8Z 0 |1   S in |2
Page 6 of 11
(12.5),(12)
2. PL: Time-average power delivered to the load. This quantity is
similar to (11):
| V2 |2
PL 
(12.6),(13)
1 |  L |2 

2Z 0
Using (5) and (10) in (13), as shown in the text,
2
2
1

|

|
|1


|


| VS |2
L
S
| S21 |
PL 
(12.7),(14)
8Z 0
|1  S 22 L |2 |1   S  in |2
3. Pav,s: Maximum available power from the source (and
supplied to the circuit). This occurs when Z in  Z S*   in  *S
(i.e., conjugate match). So, from Pin in (12) and with in  *S :
2
2
| VS |2 |1   S | 1 |  S | 
Pav , S  Pin | * 
in
S
8Z 0
|1 |  S |2 |2
But with |1 |  S |2 |2  1 |  S |2  then
2
Pav , S
| VS |2 |1   S |2

8Z 0 1 |  S |2
(12.9),(15)
4. Pav,n: Maximum available power from the network (and
supplied
to
the
load).
This
occurs
when
*
Z L  Z out
  L  *out (i.e., conjugate match). From (14)
and with  L  *out :
Whites, EE 481/581
Lecture 33
Page 7 of 11
2
2
1

|

|
|1


|


| VS |2
out
S
Pav ,n  PL  * 
| S 21 |
L
out
8Z 0
|1  S 22*out |2 |1   S in |2
Using (6) and after considerable algebra, it can be shown that
| VS |2
|1   S |2

Pav ,n 
(12.11),(16)
| S 21 |
2
2
8Z 0
|1  S11 S | 1 |  out | 
With these four time-average power quantities in (12) and (14)(16), we are now in a position to compute the three power gain
expressions.
 Operating Power Gain, G. From (1) and substituting (12) and
(14):
2
2
2




1
|
|
|1
|
|1



|


PL
L
S
S
in
G
| S 21 |2
Pin
|1  S 22 L |2 |1   S in |2 |1   S |2 1 |  in |2 
or
1
1 |  L |2
2
| S 21 |
G
2
1 |  in |
|1  S 22 L |2




Source end
(12.8),(17)
Load end
 Available Gain, GA. From (2) and substituting (15) and (16):
Pav ,n
1 |  S |2
1
2
|
|
GA 

S
(12.12),(18)
21
2
2
1 |  out |
Pav , S |1  S11 S |
 Transducer Gain, GT. From (3) and substituting (14) and (15):
1 |  S |2
1 |  L |2
PL
2

| S 21 |
GT 
(12.13),(19)
|1  S 22 L |2
Pav , S |1   S  in |2
Whites, EE 481/581
Lecture 33
It can also be shown that GT can be expressed as
PL
1 |  S |2
1 |  L |2
2
GT 
| S 21 |

2
Pav , S |1  S11 S |
|1   out  L |2
Page 8 of 11
(20)
Discussion
(i)
All of these gain expressions (17)-(20) are formed by the
product of three factors. The first and third describe how
the power gain is reduced (or accentuated) by the source
and load circuits, respectively.
(ii) G and GA contain portions of GT. More specifically, the last
two terms in G are the same as those in (19), while the first
two terms in GA are the same as those in (20).
(iii) It is apparent from (17) that G is not dependent on ΓS (or
ZS). From (18) we deduce that GA is not dependent on ΓL
(or ZL). However, GT is dependent on both ΓS and ΓL.
(iv) If the source and load are both conjugate matched, (i.e.,
in  *S and  out  *L ) then G  GT in (19) and GA  GT
in (20) such that
G  GT  GA  | S 21 |2 
(21)
(v) If  S   L  0 (i.e., the source and load are matched for
zero reflection rather than conjugate matched) then from
(19)
2
GT  S 21
(22)
Whites, EE 481/581
Lecture 33
Page 9 of 11
| S21 |2
| S21 |2
while G 
and GA 
.
2
2
1 | in |
1 |  out |
Example N33.1. (Similar to text example 12.1.) The input and
output matching networks shown below are designed to produce
 S  0.5120 and  L  0.490 . Calculate G, GA, and GT given
the following S parameters for the transistor.
S11  0.6  160 , S12  0.04516
S 21  2.530
, S 22  0.5  90
Z S Z in
 S in
 From (6),
 in  S11 
Z out Z L
 out  L
 L S12 S21
1   L S22
0.490  0.04516  2.530
 0.6  160 
1  0.490  0.5  90
 in  0.627  164.6

 From (7),
Whites, EE 481/581
Lecture 33
 out  S 22 
Page 10 of 11
 S S12 S 21
1   S S11
0.5120  0.04516  2.530
 0.5  90 
1  0.5120  0.6  160
 0.471  97.6

 out
With these reflection coefficients and the given S parameters, we
can now compute the requested gain quantities.
 From (17),
1
1 |  L |2
2
| S 21 |
G
1 |  in |2
|1  S 22 L |2
1
1  0.42
2
2.5

2
1  0.627
|1  0.5  90  0.490 |2
G  13.52
11.31 dB 
 From (18),
1 |  S |2
1
2
|
|
GA 

S

21
|1  S11 S |2
1 |  out |2
1  0.52
1
2
2.5



|1  0.6  160  0.5120 |2
1  0.4712
GA  9.56
 From (19),
 9.80 dB 
Whites, EE 481/581
Lecture 33
Page 11 of 11
1 |  S |2
1 |  L |2
2
GT 
 | S 21 | 
|1   S in |2
|1  S22 L |2
1  0.52

 2.52 

 2
|1  0.5120  0.627  164.6 |
1  0.42
 9.44

 2
|1  0.5  90  0.490 |
Observe that
while
 9.75 dB 
PL
P
 Pin  L
Pin
13.52
P
P
GT  9.44  L  Pav , S  L
Pav , S
9.44
G  13.52 
We see from these two equations that Pin  Pav , S . Hence, we can
deduce that because G  GT , then the input power, Pin, is less
than the maximum power available from the source, Pav,S.
Additionally, with
and
GA 
Pav ,n
 9.56
Pav , S
P
GT  L  9.44
Pav , S
we can deduce that nearly all of the power available from the
network is delivered to the load.