* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 5.2 Bisectors of Triangles
Golden ratio wikipedia , lookup
Approximations of π wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
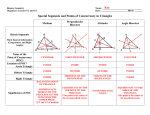
Adv. Geometry 5.2 Perpendicular and Angle Bisectors Objective: Prove and apply properties of perpendicular and angle bisectors of a triangle. The circumcenter can be inside the triangle, outside the triangle, or on the triangle. The circumcenter of ∆ABC is the center of its circumscribed circle. A circle that contains all the vertices of a polygon is circumscribed about the polygon. 1. Find GM 2. Find GK 3. Find JZ A triangle has three angles, so it has three angle bisectors. The angle bisectors of a triangle are also concurrent. This point of concurrency is the INCENTER OF THE TRIANGLE. Unlike the circumcenter, the INCENTER is always inside the triangle. The incenter is the center of the triangle’s inscribed circle. A circle INSCRIBED in a polygon intersects each line that contains a side of the polygon at exactly one point. Hw ws 5.2