* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 3.1: Identify Pairs of Lines and Angles
Survey
Document related concepts
Transcript
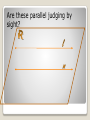
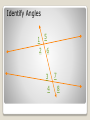
Chapter 3.1: Identify Pairs of Lines and Angles What angle pairs are formed by transversals? M11.B.2.1, M11.C.1.2 Parallel lines ◦ never intersect ◦ are coplanar ◦ The symbol for parallel lines is || ◦ If line l l is parallel to line m you can represent it with || m. ◦ When 2 drawn lines are parallel there will be little arrows or triangles on the lines. Are these parallel judging by sight? Are these parallel? Are these parallel? Are these parallel? Parallel planes are two planes that do not intersect. Parallel Planes Perpendicular Planes are planes that intersect at a 90˚ angle. Perpendicular Planes Skewed lines do not intersect, but are not coplanar. The last 2 examples were examples of skewed lines. Skewed Lines Parallel Postulate If there is a line and a point not on that line, then you can draw only 1 line parallel to the line that passes through that point. Not parallel . Perpendicular Postulate If there is a line and a point, then there is one line that passes through the point that is perpendicular to the line. . Not Perpendicular Page 150 # 3-10 Transversals Transversals are lines that intersect two or more coplanar lines at different points. In other words a line that intersects 2 other lines. transversal There are 4 different angle relationships created by a transversal Corresponding angles: same side of transversal and of the individual lines. (angles 2 and 6) Alternate interior: angles on the inside of the 2 lines, but on either side of the transversal. (angles 4 and 5) Alternate exterior: angles on the outside of the lines, but on opposite sides of the transversal. (angles 1 and 8) Consecutive interior: angles on the inside of the lines and on the same side of the transversal. (angles 3 and 5) Identify Angles 1 5 2 6 3 4 7 8