* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Sect. 12-4 Inscribed Angles
Survey
Document related concepts
Transcript
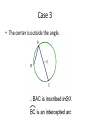
Sect. 12-4 Inscribed Angles Geometry Honors What and Why • What? – Find the measure of inscribed angles and the arcs they intercept. • Why? – To use the relationships between inscribed angles and arcs in real-world situations, such as motion pictures. Recall Central Angle • A central angle is an angle whose vertex is the center of the circle. • The arc formed by a central angle is the same measure as the angle. Inscribed Angles • The vertex of ∠𝐶 is on the circle, and the sides of ∠𝐶 are chords of the circle. • ∠𝐶 is an inscribed angle. 𝐴𝐵 is the intercepted arc of ∠C. Measuring Inscribed Angles • A polygon is inscribed in a circle if all its vertices lie on the circle. – ∆𝐷𝐸𝐹 is inscribed in circle Q. – Circle Q is circumscribed about ∆𝐷𝐸𝐹 Example • Which arc does ∠𝐴 intercept? • Which angle intercepts 𝐷𝐴𝐵? • Is quadrilateral ABCD inscribed in the circle or is the circle inscribed in ABCD? Theorem 12-10 Inscribed Angle Theorem • The measure of an inscribed angle is half the measure of its intercepted arc. • 𝑚∠𝐵 = 1 𝑚𝐴𝐶 2 There are three cases of this theorem to consider. Case 1: • The center is on a side of the angle. Case 2 • The center is inside the angle. Case 3 • The center is outside the angle. Example • Find the values of a and b in the diagram. Corollaries • Corollary 1 – Two inscribed angles that intercept the same arc are congruent. • Corollary 2 – An angle inscribed in a semicircle is a right angle. • Corollary 3 – The opposite angles of a quadrilateral inscribed in a circle are supplementary. Examples • Find the measure of the numbered angle. • In the diagram, B and C are fixed points, and point A moves along the circle. From the Inscribed Angle Theorem, you know that as A moves, 𝑚∠𝐴 remains the same, and that 1 𝑚∠𝐴 = 𝑚𝐵𝐶. This is also true when A and C 2 coincide. Theorem 12-11 • The measure of an angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc. Example • 𝐾𝐽 is tangent to the circle at J. Find the values of x, y and z.