Download Measurements and Their Analysis

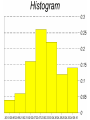
Measurements and Their Analysis
Introduction
• Note that in this chapter, we are talking
about multiple measurements of the same
quantity
• Numerical analysis – computation of
statistical quantities (mean, variance, etc.)
• Graphical analysis – construction of bar
charts, scatter diagrams, etc.
Sample Versus Population
• Most often, we collect a small data sample
from a much larger population
• For example, say we wanted to determine
the ratio of female to male students enrolled
at UF
• Theoretically we could visit every UF
student and collect this information – then
compute the ratio
• This would be an assessment of the
population, which gives the actual ratio
Sample of Students
• Visiting every UF student would take a very
long time, so we might collect a smaller
sample (perhaps stand by the union for 10
minutes and count students as they walk by)
• If we compute the ratio from this sample,
we would get an estimate of the actual ratio
• It is important to be unbiased
• If we based our sample on students in this
room, we would get a biased estimate
Sample of Measurements
• The population size for measurements is
infinite
• Thus, we are always dealing with samples
when analyzing measurements
Now, let’s look at some analysis methods
for samples of measurements.
Range and Median
• The range (sometimes called dispersion) is
the difference between the largest and
smallest values
• Generally, a smaller range implies better
precision
• The median is the middle value of a sorted
data set
• When the number of data elements is even,
take the mean of the two middle values
Ordered Set of 50 Readings
20.1
21.9
22.5
22.8
23.1
23.5
23.8
24.2
24.8
25.4
20.5
22.0
22.6
22.9
23.2
23.6
23.9
24.3
25.0
25.5
21.2
22.2
22.6
22.9
23.2
23.7
24.0
24.4
25.2
25.9
21.7
22.3
22.7
23.0
23.3
23.8
24.1
24.6
25.3
25.9
21.8
22.3
22.8
23.1
23.4
23.8
24.1
24.7
25.3
26.1
Range = 26.1-20.1 = 6.0
Median is 23.45 (the average
of 23.4 and 23.5)
Note that the difference
between the lowest value and
the median is 3.35 and
between the highest and the
median is 2.65
Frequency Histogram
• The frequency histogram (or simply histogram)
is a graphical representation of data
• A histogram is a bar graph that illustrates the
data distribution
• To produce a histogram, the data are divided
into classes which are subranges that are
usually equal in width
• The number of classes can vary depending on
the number of values, but odd numbers like 7,
9, or 11 are often good choices
Dividing Data Into Classes
Say we want to construct a histogram of the previous data set
using 7 classes spanning the range.
The class width will be 6.0/7 = 0.857143 = 0.86
Therefore the first class subrange will be 20.10 – 20.96, the
second subrange will be 20.96 – 21.81, the third will be 21.81 –
22.67, etc.
We then count the number of values falling within those classes
and compute the fraction of the total.
Class Frequency Table
Class
interval
20.10 - 20.96
20.96 - 21.81
21.81 - 22.67
22.67 - 23.53
23.53 - 24.39
24.39 - 25.24
25.24 - 26.1
Class
frequency
2
3
8
13
11
6
7
Class relative
frequency
2/50 = 0.04
3/50 = 0.06
8/50 = 0.16
13/50 = 0.26
11/50 = 0.22
6/50 = 0.12
7/50 = 0.14
Σ= 50/50 = 1
What Can We Judge From a
Histogram?
•
•
•
•
Symmetry
Range
Frequencies
Steepness indicates precision, but only if the
histograms have the same class intervals
and scales
What might cause these various shapes?
Numerical Measures
• Measures of central tendency
• Measures of data variation
Measures of Central Tendency
• Arithmetic mean or average
• Median (mentioned previously)
• Mode
Arithmetic Mean
n
y
y
i 1
i
n
y
is the sample mean
n
is the number of values
yi
are the individual values
μ is the population mean but the same formula is used
Mean of the 50 Values
n
y
y
i 1
n
i

1175.0
 23.500
50
Why 5 significant figures?
Median
• The median is the middle value
• Half of the values are above and half are
below
• It is more effective as a measure of central
tendency when there are outliers (blunders)
in the data set
Mode
• The mode is the most frequently occurring
value
• It is seldom of use when dealing with
measurements (real numbers)
• More useful with integers (e.g. most
common age)
Definitions
• True value. A quantity’s theoretically correct or
exact value. In theory, it is the population mean, μ,
which is indeterminate for measurements
• Error (ε). The difference between a measurement
and the true value
 i  yi  
Definitions (continued)
• Most probable value ( y). Derived from a
sample, it is the average of equally
weighted measurements
• Residual (v). The difference between the
most probable value and an individual
measurement. It is similar to an error, but
definitely not the same thing
vi  y  yi
Definitions (continued)
• Degrees of Freedom. The number of observations
that are in excess of the minimum number
necessary to solve for the unknowns – it equals
the number of redundant observations
• Population variance (σ2). This quantifies the
precision of the population of a set of data. It can
also be called the mean squared error
n
 
2
2

 i
i 1
n
Definitions (continued)
• Sample variance (S2). This is an unbiased estimate
of the population variance.
n
S2 
v
i 1
2
i
n 1
• Standard error (σ). Square root of population
variance – 68.3% of all observations lie within ±σ
of the true value
Definitions (continued)
• Standard deviation (S). This is the square
root of the sample variance – it is an
estimate of the standard error. (Do not
expect 68.3% of sample observations to fall
within ±S of the sample mean unless n is
large.)
Definitions (continued)
• Standard deviation of the mean ( S y ) The
mean value will have a lower standard
deviation than any single measurement. As
n →∞, S y →0.
S
Sy 
n
Alternate Formula for Sample Variance
n
S 
2
2
(
y

y
)

i
i 1
n 1
2


  yi 
n
2
 i 1 
y

n

i
n


n
2
2
i 1
y

n
y



i

  i 1
S2 
n 1
n 1
n
Example
20.1
21.9
22.5
22.8
23.1
23.5
23.8
24.2
24.8
25.4
20.5
22.0
22.6
22.9
23.2
23.6
23.9
24.3
25.0
25.5
21.2
22.2
22.6
22.9
23.2
23.7
24.0
24.4
25.2
25.9
21.7
22.3
22.7
23.0
23.3
23.8
24.1
24.6
25.3
25.9
21.8
22.3
22.8
23.1
23.4
23.8
24.1
24.7
25.3
26.1
y  23.50
n
S
2
v
i
92.36

 1.37
n 1
50  1
i 1
What about significant figures?
By alternate form:
2
y
 i  27,704.86
27,704.86  50(23.50) 2
S
50  1
27,704.86  27,612.50
92.36
S

 1.37
50  1
49
Standard deviation of the mean
 1.37
Sy 
 0.194
50
(Note the higher precision for the mean)
Now let’s work the same example using the
program “STATS”
Was the Data Set Reasonably
Normal?
About 68% of the values should be between ±S of
the mean.
So:
23.50 ±1.37
22.13 to 24.87
34 out of the 50 values fall within that range, which
is 68%
Evaluating Normalcy of Data
• Use statistics to the extent possible
• Look for values beyond ±3S (about 99.7%
of values should be within that range from
the mean)
• At this point in the class, it is still somewhat
of a judgment call.
• Later in the course, we will look at other
methods of data evaluation