* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4-5 Isosceles and Equilateral Triangles
Multilateration wikipedia , lookup
Golden ratio wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Euler angles wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Noether's theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Four color theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
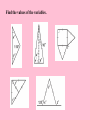
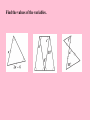
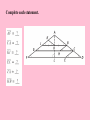
4.5 - Isosceles and Equilateral Triangles Isosceles Triangles vertex angle •The congruent sides of legs an isosceles triangles are called it legs. •The third side is the base. •The two congruent sides form the vertex base base angles angle. •The other two angles are the base angles. Theorem 4-3 Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite those sides are congruent. C A B A B Theorem 4-4 Converse of the Isosceles Triangle Theorem If two angles of a triangle are congruent, then the sides opposite the angles are congruent. C AC BC A B Theorem 4-5 The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base. C CD AB and CD bisects AB A D B A corollary is a statement that follows immediately from a theorem. Corollary to Theorem 4-3 If a triangle is equilateral, then the Y triangle is equiangular. X Y Z X Z Corollary to Theorem 4-4 If a triangle is equiangular, then the triangle is equilateral. Y XY YZ ZX X Z Find the values of the variables. Find the values of the variables. Complete each statement. Find the measure of each angle.