Download Direct Torque Control of Induction Machine Using Matrix Converter

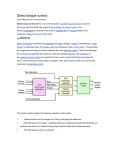
Direct Torque Control of Induction Machine Using
Matrix Converter
K. Jagadeesh1 Asst. Professor, P.V. Dhinakar Reddy2 PG Student
Dept. of EEE, Samskruthi College of Engineering & Technology, Ghatkaser, Hyderabad , Andhra Pradesh, India.
[email protected]
Dept. of EEE, Vardhaman College of Engineering & Technology., Kacharam, Shamshabad, Andhra Pradesh, India
[email protected]
Abstract
In this paper, a new control method for matrix converters is proposed which allows, under the constraint of unity
input power factor, the generation of the voltage vectors required to implement the direct torque control (DTC) of
induction machines. Using this control method, it is possible to combine the advantages of matrix converters with the
advantages of the DTC schemes. Some numerical simulations are carried out, showing the effectiveness of the proposed
method in steady-state and transient conditions. Some experimental tests were also carried out demonstrating the practical
feasibility of this control scheme.
Keywords—AC–AC Power Conversion, Induction Motor Drives, Direct Torque Control
I. Introduction
THREE-PHASE matrix converters have received considerable attention in recent years because they may become a good
alternative to voltage-source inverter pulse width-modulation (VSI-PWM) converters [1]–[6]. In fact, the matrix converter
provides bidirectional power flow, sinusoidal input/output waveforms, and controllable input power factor. Furthermore, the
matrix converter allows a compact design due to the lack of dc-link capacitors for energy storage. With reference to the
control methods, two approaches are widely used. The first one is based on transfer function analysis and has been proposed
in [1]. The second one is based on space-vector modulation (SVM) technique, which has some advantages, such as immediate
comprehension of the required commutation processes, simplified control algorithm, and maximum voltage transfer ratio
without adding third harmonic components [5], [7]–[9].
The direct torque control (DTC) technique for induction motors was initially proposed as DTC [10] or direct self-control
[11], then the method was generalized to current-source-inverter-fed induction motors and to VSI-fed and current-sourceinverter-fed synchronous machines [12]. The main advantages of DTC are robust and fast torque response, no requirements
for coordinate transformation, no requirements for PWM pulse generation and current regulators. In [13] and [14], a control
scheme for induction motors based on DTC has been analyzed, but the rotor flux is assumed as reference, instead of stator
flux, in order to achieve the highest pull-out torque. Using a VSI, different vector selection criteria can be employed to control
the torque and the flux leading to different switching strategies. Each strategy affects the drive behavior in terms of torque and
current ripple, switching frequency, and two- or four-quadrant operation capability [15]–[17]. In [18], a speed-dependent
switching strategy has been proposed in order to achieve fast torque response in a wide speed range.
In this paper, a new control method for matrix converters is proposed which allows, under the constraint of unity input
power factor, the generation of the voltage vectors required to implement the DTC of induction machines. The appropriate
switching configuration of the matrix converter is directly selected, at each sampling period, using an opportune switching
table. The table is entered by the outputs of three hysteresis controllers applied to the errors of stator flux, electromagnetic
torque, and input power factor, respectively. Using this control method, it is possible to combine the advantages of matrix
converters with the advantages of DTC schemes.
Figure.1. Schematic representation of a matrix converter
The good performance of the proposed scheme has been tested using a realistic numerical simulation of the whole drive.
The steady-state and the transient behavior have been investigated. In both cases, the results obtained emphasize the
effectiveness of the proposed drive system.
II. Direct Torque Control by Matrix Converter
A. Matrix Converter Theory
In three-phase/three-phase matrix converters, the nine bidirectional switches allow any output phase to be connected to
any input phase as schematically represented in Figure. 1.
There are 27 possible switching configurations; among these, only 21 can be usefully employed in the DTC algorithm.
These configurations are summarized in Table I. The first 18 switching configurations (named ±1, ±2 … ±9) have the
common feature of connecting two output phases to the same input phase. The corresponding output line-to-neutral voltage
vector and input line current vector, have fixed directions, as represented in Figure. 2 and 3, and will be named “active
configurations.” The magnitude of these vectors depends upon the instantaneous values of the input line-to-neutral voltages
and output line currents respectively as shown in Table I. Three switching configurations determine zero input current and
output voltage vectors and will be named “zero configurations.”
The remaining six switching configurations have the three output phases connected to a different input phase. In this
case, the output voltage and input current vectors have variable direction and cannot be usefully used.
It should be noted that the voltage vectors produced by a matrix converter can be utilized using the SVM technique to
synthesize the instantaneous voltage vector required by field-oriented control of induction motors [5]–[9].
B. Basic DTC Principles
In principle, the DTC is a hysteresis stator flux and torque control that directly selects one of the six nonzero and two
zero voltage vectors generated by a VSI (Figure. 4), in order to maintain the estimated stator flux and torque within the
hysteresis bands. In particular, the stator flux is controlled by a two-level hysteresis comparator, whereas the torque by a
three-level hysteresis comparator, as shown in Figure. 5 and 6, respectively. On the basis of the hysteresis comparator outputs
and the stator flux sector number, the most opportune VSI voltage vector is selected at each sampling period, according to the
switching table given in Table II.
Figure. 2 Output line-to-neutral voltage vector configurations
As an example, considering the stator flux vector lying in sector-1, the voltage vectors V2 and V6 can be selected in order
to increase the flux while V3 and V5 can be applied to decrease the flux. Among these, V2 and V3 determine a torque increase,
while V5 and V6 a torque decrease. The zero-voltage vectors are selected when the output of the torque comparator is zero,
irrespective of the stator flux condition. Using the switching table given in Table II, it is possible to implement DTC schemes
having good performance.
Figure. 3 Input line current vector configurations
Figure. 4 VSI output line-to-neutral voltage vectors and corresponding stator flux variations in a period ∆t
Figure. 5 Flux hysteresis comparator
TABLE 1. Switching Configurations used in the Proposed Control Scheme
C. DTC Principles Using Matrix Converters
From the previous considerations, it appears that the matrix converter generates a higher number of output voltage
vectors with respect to VSI. This feature can be utilized to keep under control a further variable in addition to stator flux and
torque. In the proposed control method, the average value of the sine of the displacement angle ψi between the input line-toneutral voltage vector and the corresponding input line current vector has been chosen as a third variable.
In principle, the proposed control technique of the matrix converter selects, at each sampling period, the proper switching
configuration, which allows the compensation of instantaneous errors in flux magnitude, and torque, under the constraint of
unity input power factor. This last requirement of the input side of the matrix converter is intrinsically satisfied if the average
value of sin(ψi) is maintained close to zero. The hysteresis regulator shown in Figure. 6 directly control this variable. The
average value of sin(ψi) is obtained by applying a low-pass filter to its instantaneous value.
The criteria utilized to implement the switching table for the matrix converter can be explained referring to an example.
We can assume that V1 is the VSI output voltage vector selected by the DTC algorithm in a given switching period. From
Figure. 2 and 4 and from Table I it appears that in order to generate a voltage vector similar to V1, one of the matrix converter
switching configurations ±1, ±2, ±3 must be chosen. The magnitude and the direction of the corresponding output voltage
vectors depend on the input line-to-neutral voltage vector. Among the six vectors, those having the same direction of V1 and
the maximum magnitude are considered. If the input line-to-neutral voltage vector lies in sector-1, then the switching
configurations, which can be utilized, are +1 and -3. Both these switching configurations satisfy the torque and flux
requirements.
As can be noted from Table I and Figure. 3, these configurations determine input current vectors lying on the directions
adjacent to sectors 1 and 4. Then, if the average value of sin(ψi) has to be decreased, the switching configuration -3 has to be
applied. On the contrary, if the average value of sin(ψi) has to be increased, the switching configuration +1 has to be applied.
The switching table based on these principles is shown in Table III. The first column contains the voltage vectors selected by
the basic DTC scheme to keep the stator flux and torque within the limits of the corresponding hysteresis bands. The other six
columns are related to the sector in which the input line-to-neutral voltage vector is lying. Depending on the output value of
the hysteresis comparator, the left or the right sub column has to be used in selecting the switching configuration of the matrix
converter. When a zero-voltage vector Cψ is required from Table II, the zero configuration of the matrix converter, which
minimize the number of commutations, is selected.
A schematic diagram of the proposed drive system is represented in Figure. 6. The reference values of torque and stator
flux are compared with the estimated values. The output of the hysteresis comparators, together with the numbers of the
sectors of the stator flux vector and input line-to-neutral voltage vector, are the input to the switching configuration selection
algorithm (Tables II and III).
Figure. 6 Block diagram of the DTC scheme with matrix converter
TABLE 3 Matrix Converter Switching Table
1
2
3
4
5
6
Cψ
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
+1
-1
V1
-3
1
2
-3
-1
2
3
-1
-2
3
1
-2
V2
9
-7
-8
9
7
-8
-9
7
8
-9
-7
8
V3
-6
4
5
-6
-4
5
6
-4
-5
6
4
-5
V4
3
-1
-2
3
1
-2
-3
1
2
-3
-1
2
V5
-9
7
8
-9
-7
8
9
-7
-8
9
7
-8
V6
6
-4
-5
6
4
-5
-6
4
5
-6
-4
5
In the lower part of the diagram are shown the estimators of electromagnetic torque, stator flux, and average value of
sin(ψi). These estimators require the knowledge of input and output voltages and currents. However, only the input voltages
and output currents are measured, while the other quantities are calculated on the basis of the switching states of the matrix
converter.
III. Numerical Simulations
The drive system proposed in this paper has been tested by some numerical simulations in order to verify the steady-state
and dynamic performance.
To analyze real phenomena such as the influence of discretization, the delay caused by the sampling of signals, and the
effects of sensors and analog-to-digital converters, a numerical simulation of the whole system has been carried out. The test
machine is a standard 3.73kW four-pole 460-V 60-Hz cage induction motor having the following parameters:
Rs=1.115Ω
Lls=0.005974H
Rr=1.083Ω
Llr=0.005974H
Lm=0.2037H
J=0.02Kg-m
Figure. 7. Input 3-Ф Supply Voltage
Figure. 8 Input 3-Ф Currents
Figure.9 Switching Pulses SAa, SBa & SCa
Figure.10 Speed response at No-Load
Figure.11 Torque profile at No-Load
Figure.12 Stator Currents
Figure.13 Rotor Currents
Figure.14 Output Voltage
Figure.15 Output Currents
Figure.16 Speed at Load condition at 0.15sec
Figure.17 Torque profile at Load of 25 N-m at 0.15sec
Figure. 18 dq-axes stator flux linkages
IV. Conclusions
In this paper, a new induction motor drive scheme has been proposed in which a matrix converter is employed in driving
an induction motor using the DTC technique. A switching table, which allows direct control of the matrix converter on the
basis of the motor control requirements, has been defined. Input line-to-neutral voltage and input line current waveforms with
25-N-m torque command. Over traditional VSI-PWM converters have been combined with the advantages of the DTC
technique. The result is a high-performance induction motor drive system with intrinsic regenerative breaking and unity input
power factor operation capability.
The proposed scheme has been tested in steady-state conditions in the low- and high-speed ranges, performing some
numerical simulation. The current and torque waveforms emphasize the effectiveness of the control scheme.
The dynamic behavior has been tested during the transient from motor to regenerative breaking operating condition. The
results show a high dynamic response with decoupled action on flux and torque. Furthermore, it has been verified that, during
the regenerative breaking, the drive system acts as a nearly sinusoidal, unity input power factor generator.
REFERENCES
A. Alesina and M. G. B. Venturini, “Analysis and design of optimum- amplitude nine-switch direct ac–ac converters,” IEEE
Trans.Power Electron., vol. 4, pp. 101–112, Jan. 1989.
[2] P. D. Ziogas, Y. G. Kang, and V. R. Stefanovic, “Rectifier-inverter frequency changers with suppressed DC link components,” IEEE
Trans. Ind. Applicat., vol. IA-22, pp. 1027–1036, Nov./Dec. 1986.
[3] D. G. Holmes and T. A. Lipo, “Implementation of a controlled rectifier using ac–ac matrix converter theory,” IEEE Trans. Power
Electron., vol. 7, pp. 240–250, Jan. 1992.
[4] C. L. Neft and C. D. Schauder, “Theory and design of a 30-Hp matrix converter,” IEEE Trans. Ind. Applicat., vol. 28, pp. 546–551,
May/June 1992.
[5] L. Huber and D. Borojevic´, “Space vector modulated three-phase to three-phase matrix converter with input power factor correction,”
IEEE Trans. Ind. Applicat., vol. 31, pp. 1234–1246, Nov./Dec. 1995.
[6] M. Kazerani and B. T. Ooi, “Feasibility of both vector control and displacement factor correction by voltage source type ac–ac matrix
converter,” IEEE Trans. Ind. Electron., vol. 42, pp. 524–530, Oct. 1995.
[7] D. Casadei, G. Grandi, G. Serra, and A. Tani, “Space vector control of matrix converters with unity input power factor and sinusoidal
input/output waveforms,” in Proc. EPE, vol. 7, Brighton, U.K., Sept.13–16, 1993, pp. 170–175.
[8] “Analysis of space vector modulated matrix converter under unbalanced supply voltages,” in Proc. SPEEDAM, Taormina, Italy, June
8–10, 1994, pp. 39–44.
[9] D. Casadei, G. Serra, and A. Tani, “Performance of SVM controlled matrix converter with input and output unbalanced conditions,” in
Proc. EPE, vol. II, Seville, Spain, Sept. 18–21, 1995, pp. 628–633.
[10] I. Takahashi and T. Noguchi, “A newquick-response and high-efficiency control strategy of an induction motor,” IEEE Trans. Ind.
Applicat., vol. IA-22, pp. 820–827, Sept./Oct. 1986.
[11] M. Depenbrok, “Direct Self-Control (DSC) of inverter-fed induction machine,” IEEE Trans. Power Electron., vol. 3, pp. 420–429,
Oct. 1988.
[12] I. Boldea and S. A. Nasar, “Torque Vector Control (TVC)—A class of fast and robust torque speed and position digital controller for
electric drives,” EMPS, vol. 15, pp. 135–148, 1988.
[13] D. Casadei, G. Grandi, and G. Serra, “Study and implementation of a simplified and efficient digital vector controller for induction
motors,” in Proc. EMD, Oxford, U.K., Sept. 8–10, 1993, pp. 196–201.
[14] “Rotor flux oriented torque-control of induction machines based on stator flux vector control,” in Proc. EPE’93, vol. 5, Brighton, U.K.,
Sept. 13–16, 1993, pp. 67–72.
[15] D. Casadei, G. Grandi, G. Serra, and A. Tani, “Effects of flux and torque hysteresis band amplitude in direct torque control of
induction machines,” in Proc. IEEE IECON’94, Bologna, Italy, Sept. 5–9, 1994, pp. 299–304.
[16] I. Ludtke and M. G. Jayne, “A comparative study of high performance speed control strategies for voltage-sourced PWM inverter-fed
induction motor drives,” in Proc. EMD’95, Durham, U.K., Sept. 11–13, 1995, pp. 343–348.
[17] Ch. Lochot, X. Roboam, and P. Maussion, “A new direct torque control strategy for an induction motor with constant switching
frequency operation,” in Proc. EPE’95, vol. 2, Seville, Spain, Sept. 18–21, 1995, pp. 431–436.
[18] D. Casadei, G. Grandi, G. Serra, and A. Tani, “Switching strategies in direct torque control of induction machines,” in Proc.
ICEM’94, Paris, France, Sept. 5–8, 1994, pp. 204–209.
[19] D. Casadei, G. Serra, and A. Tani, “Improvement of direct torque control performance by using a discrete SVM technique,” IEEE
Trans. Power Electron., vol. 15, pp. 769–777, July 2000.
[1]
K. Jagadeesh received the B.Tech (Electrical and Electronics Engineering) degree from the Jawaharlal Nehru
Technological University, Hyderabad in 2007 and pursuing M.Tech (Power Electronics) in from the Jawaharlal
Nehru Technological University, Anantapur. His field of interest includes Matrix Converters, Space Vector
Modulation, Power Electronics and Electrical & Drives and Control Systems
P V Dhinakar Reddy received the B.Tech (Electrical and Electronics Engineering) degree from the Jawaharlal
Nehru Technological University, Hyderabad in 2007 and received M.Tech (Power Electronics) in 2011 from the
Jawaharlal Nehru Technological University, Hyderabad. His field of interest includes Matrix Converters, Power
Electrical & Drives and Control Systems.