Download 5.5 notes

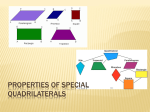
Warm Up


Elena used a rectangle, a square, a kite, a rhombus,
and an isosceles trapezoid as part of a computer
game she was creating. The player selects two of
these shapes at random. If each of the selected
shapes has at least one pair of opposite sides parallel,
the player can use these shapes as keys to a higher
level of the game. What is the probability of
selecting a pair of keys?
Represent each shape with a letter
A
Given:
B
D
C
AD is parallel to BC
m< D = 8x + 20
<A and <D are supplementary
m<A = 150 – 6x
150 - 6x + 8x +20 = 180
m<C = 12x + 60
x=5
m<D = 60
Find x
m<A = 120
Find m<B
m<C = 120
Is AB parallel to DC?
Since <D is supplementary to <A,
AB is parallel to DC.
5.5 Properties of
Quadrilaterals
Objective: identify properties of quadrilaterals
Properties of parallelograms




Opposite sides are parallel and congruent
Opposite angles are congruent
Diagonals bisect each other
Any pair of consecutive angles are
supplementary
Properties of rectangles:



All properties of parallelograms apply
All angles are right angles
Diagonals are congruent
Properties of a kite:





Two disjoint pairs of consecutive sides are congruent
Diagonals are perpendicular
One diagonal is the perpendicular bisector of the
other
One diagonal bisects a pair of opposite angles (wy
bisects <xwz and <xyz)
One pair of opposite angles are congruent (<wxy and
x
<wzy)
W
y
z
Properties of a rhombus:






All properties of parallelograms apply
All properties of a kite apply
All sides are congruent (equilateral)
Diagonals bisect the angles
Diagonals are perpendicular bisectors of each
other
Diagonals divide it into four congruent right
triangles.
Properties of a square:



All properties of a rectangle
All properties of a rhombus
The diagonals form four isosceles triangles
(45-45-90)
Properties of an isosceles trapezoid:






Legs are congruent (definition)
Bases are parallel (definition)
Lower base angles are congruent
Upper base angles are congruent
Diagonals are congruent
Lower base angle is supplementary to upper
base angle
Given: ZRVA is a parallelogram
A
AV = 2x – 4
Z
RZ = ½ x + 8
VR = 3y + 5
ZA = y + 12
Find x
Find y
Find the perimeter
V
R
Given: Rectangle MPRS
MO congruent to PO
Prove: ΔROS is isosceles
S
R
M
O
P
http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/