* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 6. Molecular vibrations
Tight binding wikipedia , lookup
Molecular orbital wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Atomic theory wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Mössbauer spectroscopy wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
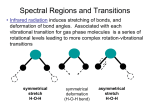
6. Molecular vibrations A molecular potential energy curve can be approximated by a parabola near the bottom of the well. The parabolic potential leads to harmonic oscillations. At high excitation energies the parabolic approximation is poor (the true potential is less confining) and is totally wrong near the dissociation limit. 6.1 Harmonic oscillator A particle undergoes harmonic motion if F= - k x, k force constant. The force F is related to the potential energy by F dV dx The parabolic potential energy of a harmonic oscillator is V = ½ k x2, where x is the displacement from equilibrium. The narrowness of the curve depends on the force constant k: the larger the value of k, the narrower the well. 1 6.1.1 Schrödinger equation and eigenvalues The SE for the oscillator is k m2 m1 d 1 2 kx E 2 dx 2 2 2 2 m is the effective or reduced mass: m1m2/(m1+m2) Quantization arises from the boundary conditions imposed by the potential: =0 at x The energy levels are: 1 E n ( n ) 2 k n =0, 1, 2, … 6.1.2 The energy levels The energy levels of a harmonic oscillator are evenly spaced with a separation ω , with w=(k/m)1/2. Even in its lowest state, an oscillator has an energy greater than zero! The separation between adjacent levels is: En 1 En The harmonic oscillator has a zero-point energy: E0 1 2 2 6.1.3 The form of the wavefunctions The normalized wavefunction and probability distribution (shown also by shading) for the lowest energy state of a harmonic oscillator. The normalized wavefunction and probability distribution (shown also by shading) for the first excited state of a harmonic oscillator. 6.1.4 The probability distributions The probability distributions for the first five states of a harmonic oscillator and the state with n=20. Note how the regions of highest probability move towards the turning points of the classical motion as n increases. ‘Mechanical oscillator’ with ‘low’ quantum number?? 3 6.3 Molecular degrees of freedom Translations: The molecule as a whole (strictly its centre of mass) moves from place to place (temperature, heat). Rotations: The molecule rotates (about its centre of mass). Vibrations: The molecule's bonds stretch, contract and bend so that the structure oscillates around the most stable configuration. Vibration is sometimes called internal motion since it is possible to define it in such a way as to separate it from translation and rotation. 6.3.1 Number of molecular vibrational modes What is the number of vibrational modes for a molecule? Each atom has 3 degrees of freedom. A molecule of N atoms has 3N degrees of freedom. There are 3 translations and-if the molecule is not linear-also 3 rotational modes. Number of vibrations for a non-linear molecule of N atoms: 3N-6 Number of vibrations for a linear molecule of N atoms: 3N-5 4 6.3.2 Translations and rotations of 3-atomic non-linear molecules http://www-biol.paisley.ac.uk/chemistry/home/staff/bstewart/teaching/inorg3/VIBSPEC/VIBSPEC3.HTM 6.3.4 Vibrational modes of 3-atomic non-linear molecules (water) symmetric stretch symmetric bend anti-symmetric stretch http://www-biol.paisley.ac.uk/chemistry/home/staff/bstewart/teaching/inorg3/VIBSPEC/VIBSPEC3.HTM 5 6.4 Selection rules The gross selection rule for the absorption of radiation by a molecular vibration is that the electric dipole moment of the molecule must change when the atoms are displaced relative to one another. Such vibrations are infrared active. Note that the molecule need not have a permanent dipole! The oscillation of a molecule, even if it is nonpolar, may result in an oscillating dipole that can interact with the electromagnetic field. 6.4.1 Example - Vibrational modes of carbon dioxide How many vibrational modes are expected for CO2 and which modes are IR active?? IR active? 3N-5 = 3x3-5=4 vibrational modes are expected for this linear molecule: no yes yes yes http://www-biol.paisley.ac.uk/chemistry/home/staff/bstewart/teaching/inorg3/VIBSPEC/VIBSPEC3.HTM 6 6.4.2 Selection rules The specific vibrational selection rule obtained from an analysis of the expression for the transition moment and the properties of integrals over harmonic oscillator wavefunctions for IR activity is: n 1 Transitions with Dn=+1 correspond to absorption and those with Dn=-1 correspond to emission. The corresponding frequencies are v E h and in the harmonic approximation there is only a single line. 6.5 Example ‘X‘-H bond The force constant of a typical X-H chemical bond is around 500 N/m. Mass of the proton is about 1.7x10-27 kg w=5.4 x 1014 1/s 5.7 10 20 J (around 360 meV) kBT at room temperature is around 25 meV, hence almost all molecules will be in their vibrational ground state and the dominant transition will be the fundamental transition, 1 0. the frequency of the transition is n=DE/h =86 THz and l=c/n = 3.5mm. Transitions between adjacent vibrational energy levels of molecules are stimulated by or emit infrared radiation. 7 6.6 Anharmonicity Real potentials are anharmonic which is taken into account in other potential models. V (1 e a ( R Re ) ) 2 The Morse potential energy curve reproduces the general shape of a molecular potential energy curve. The corresponding SE can be solved, and the values of energies obtained. The number of bound levels is finite. 6.7 Vibration-rotation spectra 6.7.1 Spectral branches Analysis of the quantum mechanics of simultaneous vibrationalrotational changes shows that DJ= ±1during the vibrational transition of a diatomic molecule. If the molecule also possesses angular momentum about its axis, then the selection rule also allows DJ=0 (as in the case of the electronic orbital angular momentum of the paramagnetic NO) When the vibrational transition n+1 n occurs, J changes by ±1 (and in some cases by 0). The absorptions then fall into three groups called branches of the spectrum: The P branch consist of all transitions with DJ=-1. The Q branch consist of all transitions with DJ=0. The R branch consist of all transitions with DJ=+1. 8 6.7.2 Example HCl A high resolution vibrationrotation spectrum of HCl. The lines appear in pairs because H35Cl and H37Cl both contribute (their abundance ratio is 3:1). There is no Q branch because DJ=0 is forbidden for this molecule. The separation between the lines in both branches gives the value of B (and hence the bond length can be deduced) 6.7.3 Vibration-rotation spectra The transitions of P, Q, and R branches in a vibration-rotation spectrum. The intensities reflect the populations of the initial rotational levels 9 6.8 Vibrational Raman spectra of diatomic molecules The gross selection rule for vibrational Raman transitions is that the polarizability should change as the molecule vibrates. Homonuclear and heteronuclear diatomic molecules are vibrationally Raman active! The specific selection rule for vibrational Raman transitions is n 1 6.8.1 Example - Vibrational modes of carbon dioxide Which of the four vibrational modes of CO2 are Raman active?? Raman active? yes no no no http://www-biol.paisley.ac.uk/chemistry/home/staff/bstewart/teaching/inorg3/VIBSPEC/VIBSPEC3.HTM 10 6.8.2 Vibration-rotation Raman spectra In gas-phase spectra, the Stokes and anti-Stokes lines have a branch structure arising from the simultaneous rotational transitions that accompany the vibrational excitations. The selection rules are DJ=0,±2 (as in pure rotational Raman spectroscopy), and give rise to the O-branch (DJ=-2), the Q branch (DJ=0), and the S branch (DJ=+2). 6.8.3 Vibration-rotation Raman spectra The transitions of O, Q, and S branches in a vibration-rotation Raman spectrum of a linear rotor. Note that the frequency scale runs in the opposite direction to that of a vibrationrotation IR spectrum, because the higher energy transitions (on the right) extract more energy from the incident beam and leave it at lower frequency. 11