Download Communicating Quantitative Information

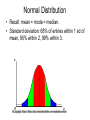
Communicating Quantitative
Information
Spreadsheets
Continue with measures of centrality. High
Stakes [Educational] Testing
Male vs. Female
Homework: Continue postings.
Complete spreadsheet assignment, if you
didn't…
Spreadsheet
• To show formulas, use ` and Ctrl. The ` is called
grave
• Different situations call for different graphs.
– Pie: parts of a whole
– Bar (or column): individual, distinct quantities. Can be
time
– Line: Time based or other continuous quantities
– X-Y: chart 2 related values
Spreadsheet
• Use HELP
• Caution: formulas use = equal sign
• Formulas can contain numbers and cell
references
• Copy-and-paste makes relative
addressing
– Always check if okay
• Apply general rule(s) of proof-read, edit,
enhance, print,…proof-read
News
• How was it to vote in primary?
• What happened in the primary? How was
it communicated? How could it have been
better?
• Other news?
Postings
• Start to think about how information could have
been better presented
– including missing information
• Stories:
–
–
–
–
–
–
Hottest summer
Emergency room
Drinking
Immigration
Tax cuts
G-7 countries debt levels
Testing: preview
• Inspired by posting in previous class
• Not enough to note how many people died
by given treatment
• How many would have died without
treatment?
• Check out articles on depression
medications causing suicides
– Initial effect of making people more
energetic…
Testing terminology
• Control group versus test/condition group
– Careful in assignments
• Double blind: neither subject nor evaluator
knows who is in what group
– Not always possible
• Most likely not possible in surgery example
• Placebo effect
– Take medicine that [you] believe will do you good
may, by itself, make you feel better
• Hawthorne effect
– Being studied improved workers
General comments on education
My view, but it is an informed view!
• Efforts should be made to improve
schools, that is, make them better.
• It is not clear that they were much better in
the past.
– Different populations, different requirements,
different outcomes for people who dropped
out.
• Think about last week's 'story': self-selected group
versus everyone taking the PSAT
Posting topics
• What was k-12 school drop out rate in
1950s, 1960s, 1970s, 1980s, 1990s, now?
– or go further back
• When did the GED begin? What are the
current absolute numbers and proportions
of GED diplomas?
• How did your k-12 school district do
recently in the NCLB testing? Regents?
…and educational testing
Problems with 'high stakes' testing
• too much time devoted to testing, not teaching and
learning
• the multiple choice/multiple guess format of most tests
'dumbs down' curriculum
– rote grading of essays also can discourage thinking
• encourages corruption
– weaker students shuffled around
– plain lies at all levels
One positive aspect of NCLB is that the rules distinguished
different groups of students and required improvement in
each category.
–
but this also could lead to corruption.
Race to the Top: claim to evaluate on improvements.
Normal Distribution
• Recall: mean = mode = median.
• Standard deviation: 68% of entries within 1 sd of
mean, 95% within 2, 99% within 3.
6 Sigma
• … name of quality in manufacturing
campaign with goal to get 99% (6 standard
deviations—3 on each side) into
acceptable range.
– Manufacture good things almost all the time
• Usually increasingly difficult to get last
amount
Inoculation campaign
• Campaign to give children in Africa polio
shots.
• Estimate made: $3 to get 90% of children.
• Students in prior class said: why can’t [UN,
NGO] pay the $3 for the remaining 10%?
• Answer?
Interlude: discrete vs continuous
• The graph showing normal distribution
represented continuous function. This is
approached by large number of data
points.
• Need to understand for a given
application/situation, are there
– a) finite number of measurements?
– b) is there something that forces the readings
to be rounded off and/or only take certain
values—quantized effect?
More on normal
• Big standard deviation says that the data
is spread out
• Small standard deviation says that most of
the data is close to the mean
– preferred situation with manufacturing: 6
sigma movement.
Male vs Female Math. ability issue
• What did the president of Harvard say?
Not clear, but one transcript of remarks
referred to the variance
• male innate ability is more spread out: more in the
'outliers', at both ends
• Draw this!
Answer
Why is variance relevant?
• The Summers issue was why there are so
few female tenured professors in the
sciences at Harvard
– This concerns the [upper] outliers, not the
mean.
Harvard president comments, cont.
• Good article about this in 1/24/05 New
York Times. Included comments:
– social forces dwarf the innate differences, if
they exist
– hard work dwarf innate differences: the AsianAmerican (parent) phenomenon
Why focus on the normal
distribution?
• Many things 'in nature' are normal.
• A normal distribution can be something
dependent on many discrete events
– binomial tends to normal
Coin toss
• Example (the example) of bi-nomial: two
choices.
– fair coin means chances equally likely. Binomial also
can refer to situations in which chances are not equal.
• Each toss is independent!
• Calculate P for probability of sequences by
multiplying
–
–
–
–
Head Head has P of (1/2) * (1/2) = ¼
Head Tail has P of (1/2) * (1/2)
=¼
Tail Head has P of (1/2)* (1/2)
=¼
Tail Tail has P of (1/2)*(1/2)
=¼
=1
Binomial Distribution
• Note: when flipping coins, any single sequence
of heads and tails is equally likely!
– HHHHHHHHHH
– HTHTHTHTHT
• There are more sequences with 5 heads and 5
tails than any other combination
– will return to this topic later. Extra credit to make a
posting explaining the formula.
• When flipping coins in a sequence (assuming a
fair coin), the odds of heads on the next flip is ½
no matter what the sequence has been.
Class Exercise
• Flip a coin 10 times. Record number of
heads.
– What are possible values?
• I will record data points and we will see the
distribution evolving…
Data collection
• Each of you will gather more data than I
will collect…
– H, T, T, H, ….. T
– count heads, count tails. Check if these two
numbers add up to 10
– Report to me how many heads.
Binomial….
• with more and more values will resemble normal
– asymptotic….tending towards
1 1
½ heads ½ tails
1 2
1
¼ 2 heads, 2/4 1 head&1 tail, ¼ 2 tail
1 3 3
1
1 4 6 4
1
1 5 10 10 5 1
1 6 15 20 15 6
1
Not everything is normally
distributed….
• Some distributions are not normal, so
need to be aware of them, also.
– mean, mode, median, standard deviation,
range still have meaning.
– bimodal, multi-modal can arise when there
are 2 or more distinct populations….
Uniform distribution
• Equal number of occurrences of each/all
values in a range
– 20, 20, 20, 21, 21, 21, 22, 22, 22, 23, 23, 23,
24, 24, 24, 25, 25, 25
– Range is 20 to 25
– What is mean? What is mode?
• Can you generalize for uniform distributions?
Gauss story
• Karl Gauss (1777-1855), was in a class with the
assignment: add up the numbers 1 to 100.
• What is the mean? For this uniform distribution,
the mean is the mean of the lowest and the
biggest numbers: 1 and 100. Mean is 101/2 is
50.5
• The sum of all the numbers is the same as if
they were each the mean: 100 * 50.5 is 5050.
Gauss story: another way
• Here are the numbers: 1, 2, 3, 4, …. 98,
99, 100
• Group numbers high and low
• 1 and 100, 2 and 99, 3 and 98, … There
are 50 pairs. Each pair adds to 101 (the
same thing!). 50 * 101 is (also) 5050.
Bi-modal
• or multi-modal. You really have two (or
more) distinct and dissimilar populations
• Consider a Purchase class attracting
mainly dance majors and football players.
Measure weight!
Correlation
• Correlation: the degree to which
measurements/variables are related.
• Can compute Pierson correlation coefficient:
-1 to 1. 0 is no correlation. Nearer to 1 or -1
shows correlation.
• Correlation coefficient values below are 1,
.85, -.94, .17
http://www.psychstat.smsu.edu/introbook/sbk17.htm
But…
• Correlation is not causality.
– Comment made about smoking and cancer,
but it has been proven that smoking causes
cancer by population studies and biological
studies.
• The damage to lungs is visible
– The cause isn't absolute—some people do
not get cancer…..
Puzzle
• 32 cards are dealt from a well-shuffled
deck of 52 cards. The deck contains 26
red and 26 black cards. What is the
difference between the number of black
cards among the 32 dealt and the red
cards remaining in the deck?
Homework
• Keep up on postings.
– can go back to old[er] topics
•
•
•
•
We will cover mortgages, subprime crisis
We will cover polls
Evaluate sources
Start to decide on topics for
– diagram project
– presentation projects