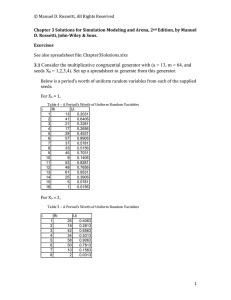
b) Use a spreadsheet to generate 1000 observations of the
... minutes and a maximum of 25 minutes, and a 75% chance that the time is distributed according to a Weibull distribution with shape of 2 and a scale of 4.5. a) Setup a spreadsheet to generate 100 observations of the service time b) Using your favorite software make a histogram of your observations ...
... minutes and a maximum of 25 minutes, and a 75% chance that the time is distributed according to a Weibull distribution with shape of 2 and a scale of 4.5. a) Setup a spreadsheet to generate 100 observations of the service time b) Using your favorite software make a histogram of your observations ...
Generating Random Variables from the Inverse Gaussian and First
... We used a linear congruential generator to produce uniformly distributed pseudo-random numbers ui on the interval (0, 1). This method uses the recursion formula xi+1 = axi (mod m), i = 0, 1, ..., n where a and m are integer constants chosen to maximize desirable properties such as independence and c ...
... We used a linear congruential generator to produce uniformly distributed pseudo-random numbers ui on the interval (0, 1). This method uses the recursion formula xi+1 = axi (mod m), i = 0, 1, ..., n where a and m are integer constants chosen to maximize desirable properties such as independence and c ...
Example 1
... Another time when we usually prefer the median over the mean (or mode) is when our data is skewed (i.e., the frequency distribution for our data is skewed). If we consider the normal distribution - as this is the most frequently assessed in statistics - when the data is perfectly normal, the mean, m ...
... Another time when we usually prefer the median over the mean (or mode) is when our data is skewed (i.e., the frequency distribution for our data is skewed). If we consider the normal distribution - as this is the most frequently assessed in statistics - when the data is perfectly normal, the mean, m ...
Sampling Distribution
... of the sample means of size _, __, and __ observations from this population. As the sample size n _________, the shape of the distributions becomes ___________. The mean μ = 1, and the standard deviation decreases taking the values 1 n . The density curve for 10 observations is ________ positively s ...
... of the sample means of size _, __, and __ observations from this population. As the sample size n _________, the shape of the distributions becomes ___________. The mean μ = 1, and the standard deviation decreases taking the values 1 n . The density curve for 10 observations is ________ positively s ...
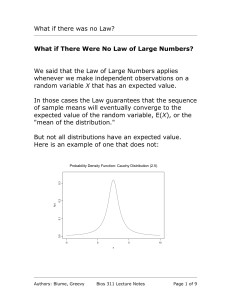
What if there was no Law? What if There Were No Law of Large
... again, this time with the normal density with mean 2.5 and standard deviation 1.5 shown for comparison. ...
... again, this time with the normal density with mean 2.5 and standard deviation 1.5 shown for comparison. ...
22S6 - Numerical and data analysis techniques Mike Peardon Hilary Term 2012
... Sample variance For n > 1 independent, identically distributed samples of a random number X, with sample mean X̄, the sample variance is n 1 X σ̄X2 = (Xi − X̄)2 n − 1 i=1 Now we quantify fluctuations without reference to (or without knowing) the expected value, μX . Note the n − 1 factor. One “degre ...
... Sample variance For n > 1 independent, identically distributed samples of a random number X, with sample mean X̄, the sample variance is n 1 X σ̄X2 = (Xi − X̄)2 n − 1 i=1 Now we quantify fluctuations without reference to (or without knowing) the expected value, μX . Note the n − 1 factor. One “degre ...
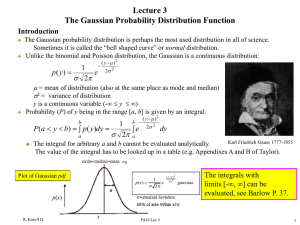
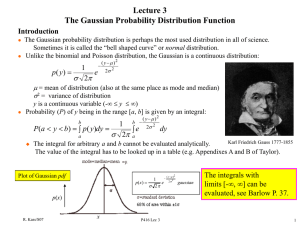
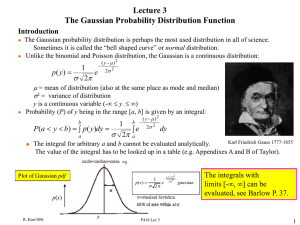
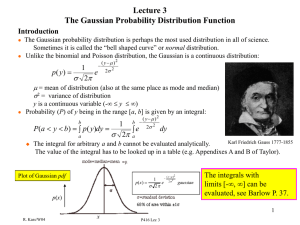
Lecture 3 Gaussian Probability Distribution Introduction
... The CLT is true even if the Y’s are from different pdf’s as long as the means and variances are defined for each pdf! u See Appendix of Barlow for a proof of the Central Limit Theorem. ...
... The CLT is true even if the Y’s are from different pdf’s as long as the means and variances are defined for each pdf! u See Appendix of Barlow for a proof of the Central Limit Theorem. ...
The Central Limit Theorem - Student Friendly Quantum Field Theory
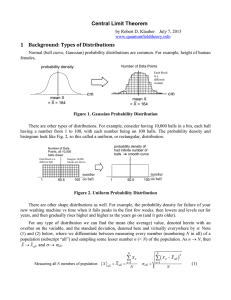
... Figure 2. Uniform Probability Distribution There are other shape distributions as well. For example, the probability density for failure of your new washing machine vs time when it fails peaks in the first few weeks, then lowers and levels out for years, and then gradually rises higher and higher as ...
... Figure 2. Uniform Probability Distribution There are other shape distributions as well. For example, the probability density for failure of your new washing machine vs time when it fails peaks in the first few weeks, then lowers and levels out for years, and then gradually rises higher and higher as ...
Chapter 4: Central Tendency
... Chapter 4: Central Tendency How do we quantify the ‘middle’ of a distribution of numbers? Three ways: The mode, median and the mean Mode (Mo): The score that occurs with the greatest frequency Example: the mode of this sample of 7 numbers: 5,3,1,6,2,8,3 is 3. ...
... Chapter 4: Central Tendency How do we quantify the ‘middle’ of a distribution of numbers? Three ways: The mode, median and the mean Mode (Mo): The score that occurs with the greatest frequency Example: the mode of this sample of 7 numbers: 5,3,1,6,2,8,3 is 3. ...
Gaussian Probability Distribution
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
Gaussian Probability Distribution
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
Gaussian Probability Distribution
... The and of the pdf must be finite. No one term in sum should dominate the sum. l A random variable is not the same as a random number. “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here ...
... The and of the pdf must be finite. No one term in sum should dominate the sum. l A random variable is not the same as a random number. “A random variable is any rule that associates a number with each outcome in S” (Devore, in “probability and Statistics for Engineering and the Sciences”). Here ...
Mean - gwilympryce.co.uk
... • Even if a variable is not normally distributed, its sampling distribution of means will be normally distributed, provided n is large (I.e. > 30) – I.e. some samples will have a mean that is way out of line from population mean, but most will be reasonably close. – “Central Limit Theorem” ...
... • Even if a variable is not normally distributed, its sampling distribution of means will be normally distributed, provided n is large (I.e. > 30) – I.e. some samples will have a mean that is way out of line from population mean, but most will be reasonably close. – “Central Limit Theorem” ...