Probability with Engineering Applications
... mathematical model. The notation that we use to frame a problem can be critical to understanding or solving the problem. There are often events, or variables, that need to be given names. Probability theory is widely used to model systems in engineering and scientific applications. These notes adopt ...
... mathematical model. The notation that we use to frame a problem can be critical to understanding or solving the problem. There are often events, or variables, that need to be given names. Probability theory is widely used to model systems in engineering and scientific applications. These notes adopt ...
Chapter 3: Basic Monte Carlo Methods
... an accurate measure of time, or the amount of background cosmic radiation as the basis for such a generator, but these suffer from a number of disadvantages. They may well be “random” in some more general sense than are the pseudo-random number generators that are presently used but their properties ...
... an accurate measure of time, or the amount of background cosmic radiation as the basis for such a generator, but these suffer from a number of disadvantages. They may well be “random” in some more general sense than are the pseudo-random number generators that are presently used but their properties ...
Part III: Monte Carlo Methods
... Middle Square (John Von Neumann, 1946) To generate a sequence of 10 digit integers, start with one, and square it amd then take the middle 10 digits from the answer as the next number in the sequence. eg. 57721566492=33317792380594909291 so the next number is given by ...
... Middle Square (John Von Neumann, 1946) To generate a sequence of 10 digit integers, start with one, and square it amd then take the middle 10 digits from the answer as the next number in the sequence. eg. 57721566492=33317792380594909291 so the next number is given by ...
The binomial theorem
... So the answer is 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40 320 ways. The notation for this is 8!. This is read as eight factorial. Most calculators have a factorial key. The number of ways to arrange n different objects in a row is n!. It is important to note that n! = n(n − 1)!. For this statement to be t ...
... So the answer is 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 40 320 ways. The notation for this is 8!. This is read as eight factorial. Most calculators have a factorial key. The number of ways to arrange n different objects in a row is n!. It is important to note that n! = n(n − 1)!. For this statement to be t ...
b) Use a spreadsheet to generate 1000 observations of the
... distribution. Generate 100 observations of X using a spreadsheet. a) Estimate the mean from your observations. Report a 95% confidence interval for your point estimate. b) Estimate the variance from your observations. Report a 95% confidence interval for your point estimate. c) Estimate the P{X ≥ 3} ...
... distribution. Generate 100 observations of X using a spreadsheet. a) Estimate the mean from your observations. Report a 95% confidence interval for your point estimate. b) Estimate the variance from your observations. Report a 95% confidence interval for your point estimate. c) Estimate the P{X ≥ 3} ...
File
... Since (1 − 2 x)5 = 1 − 5(2 x) + 10(4 x 2 ) − 10(8 x 3 ) + " = 1 − 10 x + 40 x 2 − 80 x 3 + " the x 3 term in (1 + x + 2 x 2 )(1 − 2 x)5 is given by the sum of 1( −80 x 3 ) , x(40 x 2 ) and 2 x 2 (−10 x) . So the coefficient of x 3 is −80 + 40 − 20 = −60 . ...
... Since (1 − 2 x)5 = 1 − 5(2 x) + 10(4 x 2 ) − 10(8 x 3 ) + " = 1 − 10 x + 40 x 2 − 80 x 3 + " the x 3 term in (1 + x + 2 x 2 )(1 − 2 x)5 is given by the sum of 1( −80 x 3 ) , x(40 x 2 ) and 2 x 2 (−10 x) . So the coefficient of x 3 is −80 + 40 − 20 = −60 . ...
Bernoulli trial
... · seek the probability of 2 successes out of 3 trials · there are three ways in which this can happen · SSF · SFS · FSS · the binomial coefficient for C(3,2)=3 multiples the probability pkqn-k to correct for the fact that the outcome may manifest itself in more than one way ...
... · seek the probability of 2 successes out of 3 trials · there are three ways in which this can happen · SSF · SFS · FSS · the binomial coefficient for C(3,2)=3 multiples the probability pkqn-k to correct for the fact that the outcome may manifest itself in more than one way ...
November 2003 examination
... selecting a driver and simulating one year is repeated N times. In the second actuary’s simulation, a driver is selected and N years of experience are generated for that driver. Which of the following is/are true? I. The ratio of the number of claims the first actuary simulates to the number of clai ...
... selecting a driver and simulating one year is repeated N times. In the second actuary’s simulation, a driver is selected and N years of experience are generated for that driver. Which of the following is/are true? I. The ratio of the number of claims the first actuary simulates to the number of clai ...
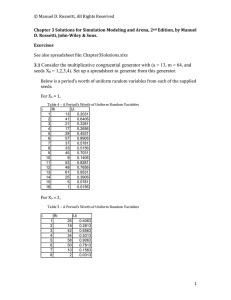
2.10 Consider the following sequence of (0,1) random numbers
... (a) __________________ (b) _____________________ (c)_________________ (a) inverse transform, (b) convolution, (c) acceptance/rejection 2.3 Consider the multiplicative congruential generator with (a = 13, m = 64, and seeds X0 = 1,2,3,4) a) Does this generator achieve its maximum period for these para ...
... (a) __________________ (b) _____________________ (c)_________________ (a) inverse transform, (b) convolution, (c) acceptance/rejection 2.3 Consider the multiplicative congruential generator with (a = 13, m = 64, and seeds X0 = 1,2,3,4) a) Does this generator achieve its maximum period for these para ...
The Binomial Theorem
... of the powers using the Binomial Theorem: (a + b)1 = 1a1 + 1b1. If n = 2, use row 2 of Pascal’s Triangle and the pattern of the powers: (a + b)2 = 1a2 + 2a1b1 + 1b2. If n = 3, use row 3 of Pascal’s Triangle and the pattern of the powers: (a + b)3 = 1a3 + 3a2b1 + 3a1b2 + 1b3. 2.2.3: The Binomial Theo ...
... of the powers using the Binomial Theorem: (a + b)1 = 1a1 + 1b1. If n = 2, use row 2 of Pascal’s Triangle and the pattern of the powers: (a + b)2 = 1a2 + 2a1b1 + 1b2. If n = 3, use row 3 of Pascal’s Triangle and the pattern of the powers: (a + b)3 = 1a3 + 3a2b1 + 3a1b2 + 1b3. 2.2.3: The Binomial Theo ...
X - Physics
... Continuous Probability: In this case P can be any number between 0 and 1. We can define a “probability density function”, pdf, f (x) f x dx dP x a x dx with a a continuous variable The probability for x to be in the range a x b is: ...
... Continuous Probability: In this case P can be any number between 0 and 1. We can define a “probability density function”, pdf, f (x) f x dx dP x a x dx with a a continuous variable The probability for x to be in the range a x b is: ...