* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
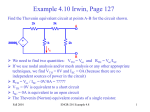
Download In the circuit shown below, the switch closes at t = 0. a) Find iL(t → ∞).
Galvanometer wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Power electronics wikipedia , lookup
Operational amplifier wikipedia , lookup
Electrical ballast wikipedia , lookup
Crossbar switch wikipedia , lookup
RLC circuit wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Surge protector wikipedia , lookup
Power MOSFET wikipedia , lookup
Opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
QUIZ 4 PROBLEM 1 SOLUTION 1250 F 14 EX: In the circuit shown below, the switch closes at t = 0. a) Find iL (t → ∞) . b) Write a numerical expression for iL (t > 0) c) Find the time, t1, when the energy stored in the inductor has dropped by 1/e2 compared to its initial value at t = 0. That is, find t1 such that w (t = 0) wL (t1 ) = L 2 . e SOL'N: a) As time approaches infinity, the switch is closed, and the L acts like a wire (because current is no longer changing implies v = Ldi/dt = 0 V). The switch bypasses the current source and resistor. If we consider a voltage loop around the outside, we have only R2. Thus, the voltage drop across R2 must be zero. It follows from Ohm's law that the current in R2 must be zero. Since the current in R2 is the same as the current in L, we must have zero current in L as time approaches infinity. iL (t → ∞) = 0 A b) We use the general solution for iL(t): i(t) = [i(t = 0+ ) − i(t → ∞)]e−t / τ + i(t → ∞) where τ = L/RTh where RTh is the Thevenin equivalent resistance as seen from the terminals where L is connected. Since we have only an independent source, we may turn off the source and look into the circuit to find the Thevenin equivalent resistance: We see only R2, since the switch, being closed, bypasses the current source and R1. RTh = R2 and τ = L / RTh = 200 µH 20 = ns ! 6.7 ns 30 kΩ 3 To find the initial current in L, we consider the circuit at time t = 0–. The switch is open just before the switch is closed, and the L acts like a wire. Inspection of the circuit reveals that it is a current-divider. iL (t = 0 − ) = is R1 20 kΩ = 10 mA = 4 mA R1 + R2 30 kΩ + 20 kΩ We substitute into the general solution to obtain our answer: iL (t) = [iL (t = 0 + ) − iL (t → ∞)]e−t /τ + iL (t → ∞) or iL (t) = [4 mA − 0]e−t /6.67 ns + 0 = 4e−t /6.67 ns mA c) The energy stored in L is proportional to the square of iL(t): wL (t) = 1 2 LiL (t) 2 Given the answer to part (b), we can write the energy as follows: wL (t) = 2 1 2 1 ⎡ L iL (t = 0)e−t /τ ⎤ = LiL2 (t = 0) ⎡ e−t /τ ⎤ ⎦ ⎣ ⎦ 2 ⎣ 2 wL (t) = 1 2 LiL (t = 0)e−2t /τ . 2 or If we want to scale the energy by a factor of 1/e2 = e–2, we need only choose t = 2τ. Thus, our answer is t = τ ! 6.67 ns