Download Power factor at the load

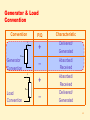
FUNDAMENTAL OF ELECTRICAL POWER
SYSTEMS (EE 270)
Chapter 3
Basic Principles
1
Objectives
• Review basic concepts and establish
terminology and notation encountered in
electric circuit theory.
• Review phasors, instantaneous power,
complex power, network equations and
elementary aspects of balance threephase circuits.
2
Power System
Network
3
Three-Phase
Power Transformer
4
Sub-station
5
Distribution
Transformer
6
Phasors
• Sinusoidal voltage or current at constant
frequency characterized by:
– Phase angle
– Maximum value
Instantane ous Voltage : v(t )  Vmax cos(t   v )
Instantane ous Current : i(t )  I max cos(t   i )
7
Phasors
• The root-mean-square  effective value
• Let the rms value of
Voltage:
Current:
Vm
V 
2
• And let
Im
I 
2
  V   i
8
Power in Single
Phase AC Circuit
Assume a single phase sinusoidal source supplying a load.
v(t) = instantaneous voltage
i(t) = instantaneous current
Find the instantaneous power p(t)
9
Power in Single
Phase AC Circuit
p(t )  v(t )i (t )
 Vm I m cost   v  cost   i 
.
.
.
 V I cos   V I sin 
Use
trigonometric
identity
cos A cos B 
1
1
cos( A  B)  cos( A  B)
2
2
10
Power in Single
Phase AC Circuit
p(t )  v(t )i (t )
 Vm I m cost   v  cost   i 
11
Real Power
• The average power, P is also referred as
the active power or real power.
• The power absorbed by the resistive
component of the load.
• Standard unit: Watt
P  V I cos
12
Reactive Power
• The power absorbed by the reactive
component of the load.
• Standard unit: var (volt-ampere reactive)
Q  V I sin 
13
Complex Power
• The complex power, S is the product of
voltage and the conjugate of the current.
• Standard unit: VA (volt-ampere)
S  P  jQ
S  P Q
2
2
14
Complex Power
S  VI *
 V v I   i   VI v   i 
 VI cos v   i   jVI sin  v   i 
 VI cos   jVI sin 
 P  jQ
15
Phasor Diagram
Purely Resistive Load
Q=0; S=P
Purely Inductive Load
P=0
V
I

i
v
Purely Capacitive Load
P=0
I
V

i
v
16
Phasor Diagram
17
Power Triangle
Purely Inductive Load
P=0, Q=+ve
S
Q

P
Purely Capacitive Load
P

Q
S
P=0, Q=-ve
18
Power Triangle
19
Impedance
• Impedance of complex power is given by:
2
V
Z *
S
20
The Complex
Power Balance
• The sum of real and reactive power
supplied by the source is equal to the
sum of real and reactive powers
transferred to the load.
• Law of energy conservation
S
source
  Sload
21
The Complex
Power Balance
I
I3
I2
I1
Z1
Z3
Z2
V
S  VI  V  I1  I 2  I 3   VI  VI 2  VI
*
*
*
1
*
*
3
22
The Complex
Power Balance
Example:
V  12000
Z1  60  j 0
I
I1
I2
I3
Z1
V
Z2
Z3
Z 2  6  j12
Z3  30  j 30
Total load complex power , S ?
23
Solution
Current at each load:
V 12000
 20  j 0 A

I1 
60  j 0
Z1
V 12000
 40  j80 A

I2 
6  j12
Z2
V 12000
 20  j 20 A

I3 
Z 3 30  j 30
24
Solution
Complex power absorbed at each load:
S1  VI1*  120020  j 0  24kW
S 2  VI 2 *  120040  j80  48kW  j 96k var
S3  VI 3 *  120020  j 20  24kW  j 24k var
Total load complex power:
Stotal  S1  S 2  S3  96kW  72k var
25
Exercise
Two loads connected in parallel are
supplied from a single-phase 240Vrms
source. The two loads draw a total real
power of 400kW at a power factor of 0.8
lagging. One of the loads draws 120kW at a
power factor of 0.96 leading. Find the
complex power of the other load.
26
Exercise
Two impedances, Z1=0.8+j5.6Ω and
Z2=8-j16Ω, and a single phase motor are
connected in parallel across a 200Vrms,
60Hz supply. The motor draws 5kVA at 0.8
pf lagging. Find S1, S2 and S3 for the motor.
27
Power Factor
Correction
PF  cos
• PF = 1 } unity power factor
• If PF<1,
apparent power |S|>real power P
• Current increase, cost of utility increase.
• Major loads of the system should be near
to unity power factor.
28
Power Factor
Correction
• Inductive load : lagging pf
• Capacitive load : leading pf
• How to fix PF? Capacitor is added to the
system (inductive load).
• PF is mostly considered in industrial
consumers (using inductive load) and not
in residential and small commercial since
the power factor is near unity.
29
Power Factor
Correction
30
Power Factor
Correction
31
Exercise
Two loads Z1=100+j0Ω and Z2=10+j20Ω are
connected across a 200Vrms, 50Hz source.
(a) Find the total real and
reactive power, the power
factor at the load, and the
total current without C. 200V
(b) Find the capacitance of
the capacitor connected
across the loads to
improve the overall power
factor to 0.8 lagging.
I
I1
100
I2
Ic
10
j 20
C
32
Solution (a)
Current at each load:
Power at each load:
2000
I1 
 20 A
100
2000
I2 
 8.945  63.43 A
10  j 20
S1  VI1*  200020
 4000VA
S 2  VI 2 *  20008.94563.43
 1.78963.43kVA
33
Solution (a)
Total real and reactive power:
S  S1  S 2  4000  178963.43
 400  800  j1600  1200  j1600VA
P  1200W
Q  1600 var
Total current without C:
S * 1200  j1600
I

 10  53.13 A
V*
2000
Power factor at the load:
PF  cos  cos53.13  0.6 lagging
34
Solution (b)
Power at the capacitor:
P  1200Watt
 new  cos 0.8  36.87
Qnew  P tan  new
1
 1200 tan 36.87  900 var
QC  Q prev  Qnew
 1600  900  700 var
35
Solution (b)
Capacitance of the capacitor:
2
SC  VI C * 
V
ZC *
2
200 2
ZC 

  j 57.14
SC * j 700
V
1
1
C 

 55.7 F
2fZC 2 5057.14
36
Exercise
Three loads are connected in parallel across a
1400Vrms, 50Hz single-phase supply.
•
•
•
Load 1: Inductive load, 125kVA at 0.28 power factor
Load 2: Capacitive load, 10kW and 40kvar
Load 3: Resistive load of 15kW
(a) Find the total kW, kvar, kVA and the supply power
factor.
(b) A capacitor of negligible resistance is connected in
parallel with the above loads to improve the power
factor to 0.8 lagging. Determine the kvar rating of
this capacitor and the capacitance in µF.
37
Exercise
Two loads are connected in parallel across a 200Vrms,
50Hz single-phase supply.
•
•
Load 1: 0.8 + j5.6Ω
Load 2: 8 - j16Ω
(a) Find the total kW, kvar, kVA and the supply power
factor.
(b) A capacitor is connected in parallel with the loads.
Find the kvar and the capacitance in µF to improve
the overall power factor to unity.
(c) What is the new line current?
38
Complex Power
Flow
• Need to consider two way current (i.e. From V1 to
V2 and from V2 to V1) and two way S (i.e. From V1
to V2 and from V2 to V1).
• If P is negative than the P in which the source is
associated to receives/absorbs the P.
• If P is positive than the P in which the source is
associated to generates/delivers the P.
• If Q is negative than the Q in which the source is
associated to receives/absorbs the Q.
• If Q is positive than the Q in which the source is
associated to generates/delivers the Q.
39
Generator & Load
Convention
Convention
P/Q
Characteristic
+
Delivered/
Generated
–
Absorbed/
Received
+
Absorbed/
Received
–
Delivered/
Generated
I
+
Vsource
Generator
Convention
–
I
+
Vload
Load
Convention
–
40
Exercise
Consider two voltage sources V1=120∟–5°V and
V2=100∟0°V are connected by a short line of
impedance Z=1+j7Ω. Determined the real and
reactive power supplied or received by each
source and the power loss in the line.
I12
V1
Zshort line
V2
41
Solution
Find current which flows from V1 to V2 i.e. I12
V1  V2 120  5  1000
I12 

 3.135  110.02 A
Z
1  j7
Find current which flows from V2 to V1 i.e. I21
V2  V1 1000  120  5
I 21 

 3.13569.98 A
Z
1  j7
Find S from V1 to V2 i.e. S12
S12  V1I12  120  5  3.135110.02   376.2105.02
*
Find S from V2 to V1 i.e. S21
S21  V I
*
2 21
 1000  3.135  69.98   313.5  69.98
42
Solution
Evaluate the source from the previous calculated S.
Based on S1:
S12  376.2105.02  97.5W  j363.3var
Source 1 receive 97.5W and delivers 363.3var.
Based on S2
S21  313.5 69.98  107.3W  j 294.5var
Source 2 generates 107.3W and receives 294.5var.
43
Solution
Power loss in the line
S L  S12  S 21   97.5  j 363.3  107.3  j 294.5
 9.8W  j 68.8 var
Check!
PL  R I12  1 3.135  9.8W
2
2
QL  X I12   7  3.135  68.8 var
2
2
Thus, the real power loss in the line is 9.8W and
the reactive power loss in the line is 68.6var.
44
Exercise
Two single-phase ideal voltage sources are
connected by a line of impedance of 0.7+j2.4Ω.
V1=500∟16.26°V and V2=585∟0°V. Find the
complex power for each source and determine
whether they are delivering or receiving real and
reactive power. Also, find the real and the reactive
power loss in the line.
45
Review..
• Power in single-phase AC
– S, P, Q, p(t)
– Phasor analysis/diagram
– Power triangle
• Complex power balance
• Power factor correction
• Complex power flow
– Generator / Load Convention
46