Download Rotation Curves:

Rotation Curves:
• We can measure rotation curves via:
–
–
–
–
HI mapping
Via optical spectroscopy H!
What are the advantages/disadvantages of each?
For HI mapping, we observe the radial velocity Vr(r,i). We
can convert this to true rotation speed V(r) via the equation
Vr(r,i) = Vsys + V(r) sin i cos "
where i is the inclination, " the azimuthal angle, and Vsys is
the systemic velocity
– Contours of constant Vr connect points of equal V(r) cos ",
producing the spider diagram
NGC 1744
Optical light and
radial velocity
contours (a
“spider” diagram)
NGC 7731
HI rotation curve
NGC 3918
H! rotation curves
two
Rotation Curves vs
Hubble type & luminosity
Rubin et al. 1985
More luminous galaxies
have higher rotation
velocities, later type galaxies
have slower rise in velocity
Typical spiral galaxies have
peak rotation velocities of
~150-300 km/s
% of R25
Rotation Curves:
For circular orbits,
mV 2 GM(r)m
=
r
r2
"
M(r) =
V 2r
G
where V is the velocity, and M(r) is the mass contained inside
an orbit of radius r. If there is no mass outside this radius,
then as r increases, M(r) remains constant, and V # r-1/2 (in
!
other words, simple Keplerian motion).
However, since a spiral galaxy’s rotational velocity is roughly
constant with radius, that means M(r) # r beyond limits of
stellar disks. (But recall that the stellar luminosity is declining
exponentially!)
Rotation Curves:
Rotation Curves:
• For rotational velocity to remain constant:
– M(r) # r
– Since the amount of visible matter is declining exponentially,
the mass must be coming from a “dark halo” that extends out
to ~100 – 200 kpc
– Since there is no visible matter to see, it is hard to measure
total masses of spirals!
– What does this imply for the density profile of the dark halo?
To first order:
dM
= 4 " r 2 # (r)
dr
V 2r
M(r) =
G
"
(assuming spherical symmetry)
dM V 2
=
dr
G
V2
V2
= 4 " r 2 # (r) $ #(r) =
G
4 " Gr 2
!
!
$ #(r) % r&2
• The rotation curves of the inner regions of spirals can be
explained by the visible mass, But in the outer regions of
spirals, dark matter is needed. So the dark halo is often
modeled via an approximation to an isothermal sphere:
"(r) =
"0
1+ (r /rc ) 2
so " # r$2 for r >> rc but " # " 0 for r << rc
• So rotation curves can be modeled using 3 components:
– an exponential disk (with constant M/L)
–! a bulge
– a dark halo
• But how does the dark halo know when to start balancing
out the contribution from the disk?? Disk-halo conspiracy!!
This looks like the outer regions of an isothermal sphere
!
HI rotation curve
NGC 7731
Broeils(1992)
Allocate as much mass to the
visible disk as possible
(assuming constant disk M/L)
Make disk M/L as small as
possible, by allocating as
much mass as possible to
the dark halo.
Allow program to find
the “best fit”)
Rotation Curves:
• In the inner regions of spirals, the rotation velocity
often increases as V # r. This implies that the angular
velocity, V/r = constant. This is solid body rotation!
• But in the outer regions, where V is constant, the
angular velocity falls off as 1/r, i.e., there is differential
rotation! In other words, two stars starting out right
next to each other on adjacent orbits will move apart
with time.
Roberts & Haynes 1994
Log<R25>
Log<LB>
Log<Mtot>
Log<Mtot/LB>
Mass to light ratios:
• By comparing the mass of a spiral (determined via the
rotation curve) to its light, we can estimate the massto-light ratio within the optical disk. These values
range from M/L ~3.7 in Sd’s to ~6.5 for S0s
• We can also integrate to find a total mass of a spiral
galaxy (at least, out to limit of its HI disk). When we
compare this to the light, we find that M/L ~ 5-25.
(But since the rotation curve is still flat, this is a lower
limit.)
• For the observed stars in a galaxy, M/L ~3, so
between 50% and 90% of a galaxy mass is in dark
matter!!
– What is it?? We’ll come back to this question later
on too.
Tully-Fisher Relation:
• Because galaxies have flat rotation curves, if one
observes all the gas in a galaxy simultaneously (i.e.,
via an integrated spectrum), its emission-line will have
a well-defined maximum-width (W)
• The width of this profile can be translated into a
velocity, via W ~ 2 Vmax sin i
– Note we need to correct W for random motions
• Tully & Fisher (1977) found that a galaxy’s maximum
rotational velocity is well-correlated with its total
#
absolute magnitude, i.e., L "Vmax where ! ~ 4
– Why is this relationship useful??
• Note that the slope & scatter change with wavelength
– Why would we!expect this?
Face-on
W
HI line profile for NGC 1744
Observed HI profile width
Tully-Fisher Relation:
Tully-Fisher at various wavelengths
• Does the TF make sense?? For a circular orbit, the rotational
velocity is caused by the gravitational forces of the mass interior
to the orbit. (This also follows from the Virial theorem.)
– V2 = GM(r)/r (yes, we’ve been here before!), thus M(r) # rV2
– Assume that all galaxies have the same M/L (is this true?).
Mass is then related to luminosity by M = L $ (M/L)
– Recall that surface brightness, I = L / 4%r2, so r #(L/I)1/2
– So, M = L $ (M/L) # r V2 # (L/I)1/2 V2
– Solving for L then yields L1/2 # V2 $ I-1/2 (M/L)-1, or
L # V4
! = 3.2
Scatter=0.25 mag
! = 3.5
Scatter=0.25 mag
log L = a log W + b
! = 4.4
Scatter=0.19 mag
(This is close to the value that is observed)
– So, Tully-Fisher works IF the surface brightness times the
mass-to-light ratio squared is constant! Or, the stars and the
dark matter are linked. Why?????
Tully-Fisher Relation:
Rotation speed is a distance-independent quantity. You can
therefore use it to infer absolute luminosity, and distance.
But using the identical data and method,
TF (1977) and ST(1976) created distance scales that differed by a factor of 2
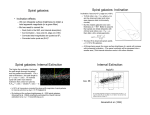
Tully-Fisher Relation: Inclination Errors
The TF is one of the most controversial (and infuriating) relations in
astronomy. Part of the problem lies with understanding errors in the
measurements. For example…
• The inclination of the galaxy, i, is related to the axis ratio b/a by
(b /a) 2 " q 2
1" q 2
• The true rotation velocity is related to the observed velocity by
cos2 i =
V = Vobs /sin i = Vobs / (1" cos 2 i)1/ 2
!
• But b/a is a measured quantity that has some uncertainty. If this
uncertainty is &b/a, then by propagation of errors
!
$
(
&
&
b /a
" V = " b / a Vobs (1# q ) %
)
2 3/2
'& (1# (b /a) ) *&
2 1/ 2
Tully & Fisher 1977
Sandage & Tammann 1976
!
Tully-Fisher Relation: Inclination Errors
The error in the true velocity explodes for galaxies that are more
face-on than ~60°. (There’s also an error associated with internal
extinction, but this is only important for the most edge-on objects.)
The Malmquist bias
Flux (or magnitude) limited samples are subject to Malmquist
(1922) bias
• There is no such thing as a perfect relation. There is
always (at least) a little bit of scatter to a relation.
• An object with luminosity L can only be seen out to a
some distance (then it becomes too faint)
• Objects that are slightly brighter than average can be
seen out to larger distances (and the converse is true for
objects that are fainter than average).
• Any flux limited sample will contain more brighter-than
average objects than fainter-than-average objects.
• The “average” brightness for objects in the sample will
be brighter than the true “average” for all objects.
The Malmquist bias
The Malmquist bias
The situation is even worse than
it sounds. While you can try to
estimate &2 for your data, you
will selectively miss fainter-than
normal objects which scatter
below your detection threshold.
The scatter you measure will be
much smaller than the true
scatter. Again, for a uniform
distribution of objects
How is the true mean absolute magnitude, M0, of a (fluxlimited) sample of objects related to the mean absolute
magnitude that is observed? The math is straightforward, but
tedious. If the objects are distributed uniformly in space, then
< M > " M0 = # 2
d ln A(m)
dm
where A(m) is the number of objects with observed apparent
magnitudes between m and m + dm. In other words, the larger
the scatter, the more you will overestimate the brightness of
!(by &2)!
objects
#
d 2 ln A(m) &
" meas = " 2 $1+ " 2
'
dm 2 (
%
!
Wars have been fought over the
true value of &.
Spiral Structure:
• There are different types of spiral arms
– “Grand-Design” – two well-defined spiral
arms (10%)
– Multiple-arm spirals (60%)
– Flocculent spirals – no well-defined arms at
all, “ratty” (30%)
• Are spiral arms leading or trailing?
• What is the nature of the arms?
Grand design spiral
Multiple arm spiral
Flocculent spiral
NGC 6946
Most spiral arms are trailing
Why are there Spiral Arms?
It only takes a few orbits for arms to become completely wound up
and lose spiral structure! This is the “winding problem”.
Density wave theory:
• We think that spiral arms are caused by a density
perturbation that moves along at a speed different from
the speed of the objects within it. The density wave
resists the spiral’s tendency to wind up and causes a
rigidly rotating spiral pattern
• Think about what happens when there is a slow-moving
car on a freeway …
• The spiral pattern is a density wave rotating through the
galaxy at a fixed angular speed, called the pattern speed
Spiral Density Waves
• When infalling gas collides with gas in the
density wave, stars formed, either due to
simple Jeans criteria collapse, or induced
through shocks.
• Material will continue to drift through the
density wave, though the local gravity
will cause a slight deceleration to the
motion.
• The high-mass stars don’t go far before
they go supernova or otherwise die. This
enhances the visibility of the density wave
at bluer wavelengths.
Spiral Density Waves
• There are initial “seed” perturbations in the
spiral disk. These come from either initial
asymmetries in the disk and/or halo (galaxy
formation processes), or induced via
galaxy encounters (like the M51 system)
• Thus there are regions of slightly higher
density than their surroundings. The
higher density accelerates matter into the
wave.
• In the inner disk, stars move faster than the
pattern speed and overtake the density
wave; in the outer disk, the density wave
overtakes the stars. Either way, material
will encounter the wave.
Spiral Density Waves
Since the brightest (bluest) stars die
before leaving the spiral arm, the spiral
density waves must show up better at
ultraviolet wavelengths.
Grand design spiral – M51
Density wave theory:
• Spiral arm pattern is amplified by resonances between
the epicyclic frequencies of the stars (deviations from
circular orbits) and the angular frequency of the spiral
pattern
– Spiral waves can only grow between the inner and outer
Lindblad resonances ('p = ' - (/m ; 'p = ' + (/m )
where ( is the epicyclic frequency and m is an integer
(the # of spiral arms)
– Stars outside this region find that the periodic pull of the
spiral is faster than their epicyclic frequency, they don’t
respond to the spiral and the wave dies out
– Resonance can explain why 2 arm spirals are more
prominent
• We observe resonance patterns in spirals
NGC 3351, inner ring
NGC 6872, inner & outer ring
Self propagating star-formation:
• Note that density wave theory does not
explain flocculent spirals. Those can be
explained by self-propagating star formation:
– Star forming regions produce supernovae, which
shocks the gas, which triggers more star formation,
etc, etc, etc
– Differential rotation stretches out the regions of star
formation into trailing, fragmentary arms
– No global symmetry (as observed)
NGC 1300, Barred galaxy
Barred Galaxies:
• In 1978 (before the discovery of dark matter), Ostriker
showed that, without a massive halo, all disk galaxies
would form bars.
• Half of all disk galaxies show a central bar which contains
up to 1/3 of the total light
• Bars are almost as flat as surrounding disks – how do we
know this?
• S0 galaxies also have bars – a bar can persist in the
absence of gas
• Bar patterns are not static, they rotate with a pattern
speed, but unlike spiral arms they are not density waves.
Stars in the bar stay in the bar.
• The asymmetric gravitational forces of a disk allow gas to
lose angular momentum (via shocks) compressing the gas
along the edge of the bar. The gas loses energy
(dissipation) and moves closer to the center of the galaxy.
ESO 510-G13, warped galaxy
What causes warps??