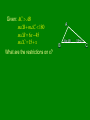* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.1 What are congruent figures?
Steinitz's theorem wikipedia , lookup
Golden ratio wikipedia , lookup
Multilateration wikipedia , lookup
Noether's theorem wikipedia , lookup
Perceived visual angle wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Four color theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
3.7 Angle-Side Theorems Objective: After studying this lesson you will be able to apply theorems relating the angle measures and side lengths of triangles. Theorem: if two sides of a triangle are congruent, the angles opposite the sides are congruent. If , then C Given: CA CT Prove: A T Statement A Reason 1. 1. 2. 2. 3. 3. 4. 4. T Theorem: if two angles of a triangle are congruent, then sides opposite the angles are congruent. If , then Y B Given: B Y Prove: OY OB O Statement Reason 1. 1. 2. 2. 3. 3. 4. 4. Theorem: If two sides of a triangle are not congruent, then the angles opposite them are not congruent, and the larger angle is opposite the longest side. 80 60 40 Longest side Theorem: If two angles of a triangle are not congruent, then the sides opposite them are not congruent, and the larger side is opposite the larger angle. Given: AC AB mB mC 180 mB 6x 45 mC 15 x What are the restrictions on x? A (6x-45) B (15+x) C Prove: The bisector of the vertex angle of an isosceles triangle is also the median to the base. O Statement Reason 1. 1. 2. 2. 3. 3. 4. 4. 5. 5. 6. 6. 7. 7. 8. 8. J K M T Given: 3 4 BX AY BW AZ B 3 4 A Prove: WTZ is isosceles Statement Reason 1. 1. 2. 2. 3. 3. 4. 4. 5. 5. 6. 6. 7. 7. 8. 8. 9. 9. W X Y Z D Given: E H EF GH Prove: DG DF Statement Reason 1. 1. 2. 2. 3. 3. 4. 4. E F G H Summary: Where is the longest side located? The shortest? If base angles are congruent what can we say about the triangle? Homework: worksheet