Download Accretion

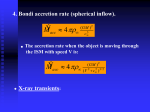
Accretion
High Energy Astrophysics
[email protected]
http://www.mssl.ucl.ac.uk/
Introduction
• Mechanisms of high energy radiation
X-ray sources
Supernova remnants
Pulsars
thermal
synchrotron
loss rotational energy
magnetic dipole
Accretion onto a compact object
• Principal mechanism for producing highenergy radiation
• Most efficient of energy production known
in the Universe.
Eacc
Mm
G
R
Gravitational
potential energy
released for body
mass M and radius R
when mass m accreted
Example - neutron star
Accreting mass m=1kg onto a neutron star:
m
neutron star mass = 1 solar mass
R = 10 km
R
=> ~1016 m Joules,
M
ie approx 1016 Joules per kg of
accreted matter - as electromagnetic radiation
Efficiency of accretion
• Compare this to nuclear fusion
H => He releases ~ 0.007 mc2
~ 6 x 1014 m Joules - 20x smaller (for ns)
Eacc
Mm
G
R
So energy released proportional
to M/R ie the more compact a
body is, the more efficient
accretion will be.
Accretion onto white dwarfs
• For white dwarfs, M~1 solar mass and
R~10,000km so nuclear burning more
efficient by factor of ~50.
• Accretion still important process however
- nuclear burning on surface => nova
outburst
- accretion important for much of lifetime
Origin of accreted matter
• Given M/R, luminosity produced depends
.
on accretion rate, m.
.
Lacc
dEacc GM dm GMm



dt
R dt
R
• Where does accreted matter come from?
ISM? No - too small. Companion? Yes.
Accretion onto AGN
• Active Galactic Nuclei, M ~ 10 9 solar mass
- very compact, very efficient (cf nuclear)
- accretes surrounding gas and stars
Fuelling a neutron star
• Mass = 1 solar mass
31
observed luminosity = 10 J/s (in X-rays)
• Accretion produces ~ 1016 J/kg
.
31
16
22
• m = 10 / 10 kg/s
~ 3 x 10 kg/year
~ 10-8 solar masses per year
The Eddington Luminosity
• There is a limit to which luminosity can be
produced by a given object, known as the
Eddington luminosity.
• Effectively this is when the inward
gravitational force on matter is balanced by
the outward transfer of momentum by
radiation.
Eddington Luminosity
M
r
m
Fgrav Frad
Mm
Fgrav  G 2 Newton
r
Accretion rate
controlled by
momentum transferred
from radiation to mass
Note that R is now
negligible wrt r
Outgoing photons from M scatter material
(electrons and protons) accreting.
Scattering
L = accretion luminosity
no. photons
crossing at r
per second
L 1

4r 2 h
photons m -2 s -1
Scattering cross-section will be Thomson
cross-section se ; so no. scatterings per sec:
Ls e
4r 2 h
Momentum transferred from photon to
particle:
h
h
e-, p
c
Momentum gained by particle per second
= force exerted by photons on particles
Ls e h
Ls e

Newton
2
2
4r h c
4r c
Eddington Limit
radiation pressure = gravitational pull
At this point accretion stops, effectively
imposing a ‘limit’ on the luminosity of a
Ls e
Mm
given body.
G 2
2
4r c
r
So the Eddington
luminosity is:
L
4cGMm
se
Assumptions made
• Accretion flow steady + spherically
symmetric: eg. in supernovae, LEdd
exceeded by many orders of magnitude.
• Material fully ionized and mostly
hydrogen: heavies cause problems and may
reduce ionized fraction - but OK for X-ray
sources
What should we use for m?
Electrostatic forces between e- and p binds
them so act as a pair.
Thus: m  m p  me  m p


4 3 108 6.67 1011.1.67 1027
LEdd 
M Joule/sec
29
6.65 10

31 M
 Joule/sec
 6.3 M Joule/sec  1.3 10 
 M SUN 
Black Holes
• Black hole does not have hard surface - so
what do we use for R?
• Use efficiency parameter, h
.
then Lacc  hMc 2
• at a maximum h = 0.42, typically h = 0.1
• solar mass bh as efficient as neutron star
Emitted Spectrum
• define temperature T rad such that h~kTrad
• define ‘effective’ BB temp T b

Tb  Lacc / 4R s
2

1/ 4
• thermal temperature, Tth such that:
M mp  me 
3
G
 2 kTth => Tth 
R
2
GMmp
3kR
Accretion temperatures
• Flow optically-thick:
Trad ~ Tb
• Flow optically-thin:
Trad ~ Tth
Accretion energies
• In general,
Tb  Trad  Tth
• For a neutron star,
• assuming
Lacc  LEdd
Tth  5.4 10 K
7
Tb  210 K
11
 M 
 J / s
 1.3 10 
 M Sun 
31
Neutron star spectrum
• Thus expect photon energies in range:
1keV  h  50MeV
• similarly for a stellar mass black hole
26
• For white dwarf, L acc ~10 J/s, M~M Sun ,
R=5x10 6 m,
6eV  h  100keV
• => optical, UV, X-ray sources
Accretion modes in binaries
ie. binary systems which contain a compact
star, either white dwarf, neutron star or
black hole.
(1) Roche Lobe overflow
(2) Stellar wind
- correspond to different types of X-ray
binaries
Roche Lobe Overflow
• Compact star M1 and normal star M2
CM
M2
+
M1
a
• normal star expanded or binary separation
decreased => normal star feeds compact
Roche equipotentials
• Sections in the orbital plane
M1
CM
+
+
M2
+
v
L1
M 2  M1
Accretion disk structure
The accretion disk (AD) can be considered as
rings or annuli of blackbody emission.
R
Dissipation rate, D(R)
0.5


3GMM
 R*  

 
1  
3
8R   R  
= blackbody flux
4
 sT ( R)
Disk temperature
Thus temperature as a function of radius T(R):
 3GMM
T ( R)  
3
 8R s
When R  R*

 3GMM
T*  
3
 8R* s
1/ 4



  R
1   
  R* 
0.5
1/ 4



 

T  T* R / R* 
3 / 4
Accretion disk formation
Matter circulates around the compact object:
ang mom
outwards
matter
inwards
• Material transferred has high angular
momentum so must lose it before accreting
=> disk forms
• Gas loses ang mom through collisions,
shocks, viscosity and magnetic fields:
kinetic energy converted into heat and
radiated.
• Matter sinks deeper into gravity of compact
object
Magnetic fields in ADs
Magnetic “flux tube”
Mag field characteristics
• Magnetic loops rise out of the plane of the
disk at any angle – the global field
geometry is “tangled”
• The field lines confine and carry plasma
across the disk
• Reconnection and snapping of the loops
releases energy into the disk atmosphere
– mostly in X-rays
• The magnetic field also transfers angular
momentum out of the disk system
Disk Luminosity
• Energy of particle with mass m in circular
orbit at R (=surface of compact object)
1
2
mv
2
=
1 GM 1
m R = 2 E acc
2
• Gas particles start at large distances with
negligible energy, thus
Ldisk =
.
MM 1
G 2R = 2 L acc
Disk structure
The other half of the accretion luminosity is
released very close to the star.
X-ray
Hot, optically-thin
inner region; emits
bremsstrahlung
UV optical
bulge
Outer regions are cool,
optically-thick and emit
blackbody radiation
Stellar Wind Model
Early-type stars have intense and highly
supersonic winds. Mass loss rates - 10-6 to
10-5 solar masses per year.
For compact star - early star binary, compact
star accretes if
GMm
1 m(v 2 + v 2 )
>
w
ns
r
2
Thus :
r acc = 2GM
v2w + v2ns
racc
bow shock
matter collects in wake
Stellar wind model cont.
• Process much less efficient than Roche lobe
overflow, but mass loss rates high enough to
explain observed luminosities.
• 10-8 solar masses per year is required to
produce X-ray luminosities of 10 31 J/s.
Magnetic neutron stars
For neutron star with strong mag field, disk
disrupted in inner parts.
Material is
channeled
along field lines
and falls onto
star at magnetic
poles
This is where most radiation is produced.
Compact object spinning => X-ray pulsator
‘Spin-up pulsars’
• Primary accretes material with angular
momentum => primary spins-up (rather
than spin-down as observed in pulsars)
• Rate of spin-up consistent with neutron star
primary (white dwarf would be slower)
• Cen X-3 ‘classical’ X-ray pulsator
Types of X-ray Binaries
Group I
Luminous (early,
massive opt countpart)
(high-mass systems)
hard X-ray spectra
(T>100 million K)
often pulsating
X-ray eclipses
Galactic plane
Population I
Group II
Optically faint (blue)
opt counterpart
(low-mass systems)
soft X-ray spectra
(T~30-80 million K)
non-pulsating
no X-ray eclipses
Gal. Centre + bulge
older, population II