* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Clustering - UTK-EECS
Survey
Document related concepts
Transcript
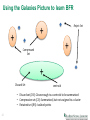
COSC 526 Class 13 Clustering – Part II Arvind Ramanathan Computational Science & Engineering Division Oak Ridge National Laboratory, Oak Ridge Ph: 865-576-7266 E-mail: [email protected] Slides inspired by: Andrew Moore (CMU), Andrew Ng (Stanford), Tan, Steinbach and Kumar Last Class • K-means Clustering + Hierarchical Clustering – Basic Algorithms – Modifications for streaming data • More today: – Modifications for big data! • DBSCAN Algorithm • Measures for validating clusters… 2 Project Schedule Updates… No. Milestone Due date 1 Selection of Topics 1/27/2015 2 Project Description & Approach 3/3/2015 3 Initial Project Report 3/31/2015 4 Project Demonstrations 4/16/2015 – 4/19/2015 5 Project Report 4/23/2015 6 Posters 4/23/2015 • Reports (2-3) will be about 1 -2 pages most, • Final report which will be between 5-6 pages typically NIPS format • More to come on posters 3 Assignment 1 updates • Dr. Sukumar will be here on Tue (Mar 3) to give you an overview of the python tools • We will keep the deadline for the assignment to be Mar 10 • Assignment 2 will go out on Mar 10 4 Density-based Spatial Clustering of Applications with Noise (DBSCAN) 5 Preliminaries • Density is defined to be the number of points within a radius (ε) – In this case, density = 9 ε • Core point has more than a specified number of points (minPts) at ε minPts = 4 core point – Points are interior to a cluster • Border points have < minPts at ε but are within vicinity of the core point border point • A noise point is neither a core point nor a border point ε 6 noise point DBSCAN Algorithm 7 Illustration of DBSCAN: Assignment of Core, Border and Noise Points 8 DBSCAN: Finding Clusters 9 Advantages and Limitations • Resistant to noise • Eps and MinPts are dependent on each • Can handle clusters of W h e n D BSCAN D oe s Nother OT W or k W e ll different sizes and – Can be difficult to shapes specify • Different density clusters within the same class can be difficult to find (MinPts=4, Eps=9.75). Original Points 10 W h ennDD BSCAN sW Nor OT We llor k W e ll W he BSCAN D oeD s oe N OT k W Advantages and Limitations (MinPts=4, Eps=9.75). Original Points (MinPts=4, Ep Original Points • •Varying density data Varying densities High-dimensional data • •High dimensional data 11 • Varying densities (MinPts=4, Eps=9.92) How to determine Eps and MinPoints • For points within a cluster, kth nearest neighbors are roughly at the same distance • Noise points are farther away in general • Plot by sorting the distance of every point to its kth nearest neighbor 12 Modifying clustering algorithms to work with large-datasets… 13 Last class, MapReduce Approach for Kmeans… In the reduce step (we get associated In the map step: • Read the cluster centers into vectors for each center): memory from a sequencefile • Iterate over each value vector and calculate the average vector. (Sum • Iterate over each cluster each vector and devide each part by •center What do we do, if we do not have sufficient for each input the number of vectors we received). memory? of new thecenter, data… • Thisall is the save it into a key/value pair.i.e., we cannot hold SequenceFile. Practical scenarios: hold a million data • •Measure the distances andwe cannot • Check the convergence between the save the nearest center which points at a given time, eachclustercenter of them being highin the key that is stored hasdimensional the lowest distance to the object and the new center. vector • If it they are not equal, increment an update counter • Write the clustercenter with its vector to the filesystem. 14 Bradley-Fayyad-Reina (BFR) Algorithm • BFR is a variant of k-means designed to work with very large, disk resident data • Assumes clusters are normally distributed around a centroid in a Euclidean space – Standard deviation in different dimensions may vary – Clusters are axis-aligned ellipses • Efficient way to summarize clusters – want memory required O(clusters) – Instead of O(data) 15 How does BFR work? • Rather than keeping the data, BFR just maintains summary statistics of data: – Cluster summaries – Outliers – Points to be clustered • This makes it easier to store only the statistics based on the number of clusters 16 Details of the BFR Algorithm 1. Initialize k clusters 2. Load a bag of points from disk 3. Assign new points to one of the K original clusters, if they are within some distance threshold of the cluster 4. Cluster the remaining points, and create new clusters 5. Try to merge new clusters from step 4 with any of the existing clusters 6. Repeat 2-5 until all points have been examined 17 Details, details, details of BFR • Points are read from disk one main-memory full at a time • Most points from previous memory loads are summarized by simple statistics • From the initial load, we select k centroids: – Take k random points – Take a small random sample and cluster optimally – Take a sample; pick a random point, and then k-1 more points, each as far as possible from the previously selected points 18 Three classes of points… • 3 sets of points, which we can keep track of • Discard Set (DS): – Points close enough to a centroid to be summarized • Compression Set (CS): – Groups of points that are close together but not close to any existing centroid – These points are summarized, but not assigned to a cluster • Retained Set (RS): – Isolated points waiting to be assigned to a compression set 19 Using the Galaxies Picture to learn BFR Reject Set + + + Compressed Set + Discard Set centroid • Discard set (DS): Close enough to a centroid to be summarized • Compression set (CS): Summarized, but not assigned to a cluster • Retained set (RS): Isolated points 20 Summarizing the sets of points • For each cluster, the discard set (DS) is summarized by: – The number of points, N – The vector SUM, whose ith component is is the sum of the coordinates of the points in the ith dimension – The vector SUMSQ: ith component = sum of squares of coordinates in ith dimension 21 More details on summarizing the points • 2d+1 values represent any clusters – d is the number of dimensions • Average in each dimension (the centroid) can be calculated as SUMi / N – SUMi = ith component of SUM • Variance of a cluster’s discard set in dimension i is: (SUMSQi / N) – (SUMi / N)2 – And standard deviation is the square root of that 22 Note: Dropping the “axis-aligned” clusters assumption would require storing full covariance matrix to summarize the cluster. So, instead of SUMSQ being a d-dim vector, it would be a d x d matrix, which is too big! The “Memory Load” of Points and Clustering • Step 3: Find those points that are “sufficiently close” to a cluster centroid and add those points to that cluster and the DS – These points are so close to the centroid that they can be summarized and then discarded • Step 4: Use any in-memory clustering algorithm to cluster the remaining points and the old RS – Use any in-memory clustering algorithm to cluster the remaining points and the old RS 23 More on Memory Load of points • DS set: Adjust statistics of the clusters to account for the new points – Add Ns, SUMs, SUMSQs • Consider merging compressed sets in the CS • If this is the last round, merge all compressed sets in the CS and all RS points into their nearest cluster 24 A few more Q1) We needdetails… a way to decide whether to put •aHow we decide if a point is discard) “close enough” newdo point into a cluster (and to a cluster that we will add the point to that BFR suggests two ways: cluster? Theneed Mahalanobis is less than threshold • We a way todistance decide whether to aput a new High into likelihood of the point belonging to point a cluster (and discard) currently nearest centroid • BFR suggests two ways: – Mahalanobis distance 1/19/2015 25 High likelihood of the point belonging to currently nearest centroid Jure Leskovec, Stanford C246: Mining Massive Datasets 44 Second way to define a “close” point • Normalized Euclidean distance from centroid • For point (x1, x2, …, xd) and centroid (c1, c2, …, cd): – Normalize in each dimension: yi = (xi-ci)/d – Take sum of squares of yi – Take the square root 26 More on Mahalanobis Distance Euclidean vs. Mahalanobis distance • If clusters are normally distributed d origin Contours of equidistant points frominthe dimensions, then after transformation, one standard deviation = sqrt(d) – i.e., 68% of points will cluster with a distance of sqrt(d) • Accept a point for a cluster if its M.D. is < some threshold, e.g. 2 standard deviations Uniformly distributed points, Euclidean distance 1/19/2015 27 Normally distributed points, Euclidean distance Jure Leskovec, Stanford C246: Mining Massive Datasets Normally distributed points, Mahalanobis distance 47 Should 2 CS clusters be combined? • Compute the variance of the combined subcluster – N, SUM, and SUMSQ allow us to make that calculation quickly • Combine if the combined variance is below some threshold • Many alternatives: Treat dimensions differently, consider density 28 Limitations of BFR… • Makes strong assumption about the data: – Normally distributed data – Does not work with non-linearly separable data – Woks only with axis aligned datasets… • Real world datasets are hardly this way 29 Clustering with Representatives (CURE) 30 CURE: Efficient clustering approach • Robust clustering approach • Can handle outliers better • Employs a hierarchical clustering approach: – Middle ground between centroid based and all-points extreme (MAX) • Can handle different types of data 31 CURE Algorithm CURE (points, k) 32 1. It is similar to hierarchical clustering approach. But it uses sample point variance as the cluster representative rather than every point in the cluster. 2. First set a target sample number c . Than we try to select c well scattered sample points from the cluster. 3. The chosen scattered points are shrunk toward the centroid in a fraction of where 0 <<1 CURE clustering procedure 4. These points are used as representative of clusters and will be used as the point in dmin cluster merging approach. 5. After each merging, c sample points will be selected from original representative of previous clusters to represent new cluster. 6. Cluster merging will be stopped until target k cluster is found Nearest Merge Merge Nearest 33 Other tweaks in the CURE algorithm • Use Random Sampling: – data cannot be stored all at once in memory – it is similar to the core-set idea • Partition and Two-pass clustering: – Reduces compute time – First, we divide the n data point into p partition and each contain n/p data point. – We than pre-cluster each partition until the number of cluster n/pq reached in each partition for some q > 1 – Then each cluster in the first pass result will be used as the second pass clustering input to form the final cluster. 34 Space and Time Complexity • Worst case time complexity: – O(n2 log n) • Space complexity: – O(n) – Using a k-d tree for insertion/updating 35 Example of how it works 36 How to validate clustering approaches? 37 Cluster validity • For supervised learning: – we had a class label, – which meant we could identify how good our training and testing errors were – Metric: Accuracy, Precision, Recall • For clustering: – How do we measure the “goodness” of the resulting clusters? 38 Clustering random data (overfitting) If you ask a clustering algorithm to find clusters, it will find some 39 Different aspects of validating clsuters • Determine the clustering tendency of a set of data, i.e., whether non-random structure actually exists in the data (e.g., to avoid overfitting) • External Validation: Compare the results of a cluster analysis to externally known class labels (ground truth). • Internal Validation: Evaluating how well the results of a cluster analysis fit the data without reference to external information. • Compare clusterings to determine which is better. • Determining the ‘correct’ number of clusters. 40 Measures of cluster validity • External Index: Used to measure the extent to which cluster labels match externally supplied class labels. – Entropy, Purity, Rand Index • Internal Index: Used to measure the goodness of a clustering structure without respect to external information. – Sum of Squared Error (SSE), Silhouette coefficient • Relative Index: Used to compare two different clusterings or clusters. 41 – Often an external or internal index is used for this function, e.g., SSE or entropy Measuring Cluster Validation with Correlation • Proximity Matrix vs. Incidence matrix: – A matrix Kij with 1 if the point belongs to the same cluster; 0 otherwise • Compute the correlation between the two matrices: – Only n(n-1)/2 values to be computed – High values indicate similarity between points in the same cluster • Not suited for density based clustering 42 Another approach: use similarity matrix for cluster validation 43 Internal Measures: SSE • SSE is also a good measure to understand how good the clustering is – Lower SSE good clustering • Can be used to estimate number of clusters 44 More on Clustering a little later… • We will discuss other forms of clustering in the following classes • Next class: – please bring your brief write up on the two papers – We will discuss frequent itemset mining and a few other aspects of clustering – Move on to Dimensionality Reduction 45























































![Data Mining, Chapter - VII [25.10.13]](http://s1.studyres.com/store/data/000353631_1-ef3a2f2eb3a2650baf15d0e84ddc74c2-150x150.png)