* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Clustering - anuradhasrinivas
Survey
Document related concepts
Transcript
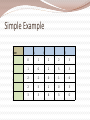
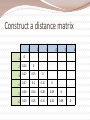
K-Means Algorithm Each cluster is represented by the mean value of the objects in the cluster Input : set of objects (n), no of clusters (k) Output : set of k clusters Algo Randomly select k samples & mark them a initial cluster Repeat Assign/ reassign in sample to any given cluster to which it is most similar depending upon the mean of the cluster Update the cluster’s mean until No Change. K-Means (graph) Step1: Step2: Form k centroids, randomly Calculate distance between centroids and each object Use Euclidean’s law do determine min distance: d(A,B) = (x2-x1)2 + (y2-y1)2 Step3: Step4: C= Assign objects based on min distance to k clusters Calculate centroid of each cluster using (x1+x2+…xn , y1+y2+…yn) n n Go to step 2. Repeat until no change in centroids. K-Mediod (PAM) Also called Partitioning Around Mediods. Step1: choose k mediods Step2: assign all points to closest mediod Step3: form distance matrix for each cluster and choose the next best mediod. i.e., the point closest to all other points in cluster go to step2. Repeat until no change in any mediods What are Hierarchical Methods? Groups data objects into a tree of clusters Classified as Agglomerative (Bottom-up) Divisive (Top-Bottom) Once a merge or split decision is made it cannot be backtracked Types of hierarchical clustering Agglomerative (Bottom-up) AGNES Places each object into a cluster and merges atomic clusters into larger clusters They differ in the definition of intercluster similarity Divisive: (Top-Bottom) DIANA All objects are initially in one cluster Subdivides the cluster into smaller and smaller pieces, until each object forms a cluster of its own or satisfies some termination condition In both of the above methods the termination condition is the number of clusters Dendogram Level 4 Level 3 Level 2 Level 1 Level 0 Measures of Distance Minimum distance – Nearest Neighbor- single linkage –minimum spanning tree Maximum distance – Farthest neighbor clustering algorithm – complete linkage Mean distance - avoids outlier sensitivity problem Average distance : can handle categorical as well as numeric data Euclidean Distance Agglomerative Algorithm Step1: Step2: Make each object as a cluster Calculate the Euclidean distance from every point to every other point. i.e., construct a Distance Matrix Identify two clusters with shortest distance. Step3: Merge them Go to Step 2 Repeat until all objects are in one cluster Agglomerative Algorithm Approaches Single Link: Quite simple Not very efficient Suffers from chain effect Complete Link More compact than those found using the single link technique Average Link Simple Example Item E A C B D E 0 1 2 2 3 A 1 0 2 5 3 C 2 2 0 1 6 B 2 5 1 0 3 D 3 3 6 3 0 Another Example Find single link technique to find clusters in the given database. 1 2 3 4 5 6 X Y 0.4 0.53 0.22 0.38 0.35 0.32 0.26 0.19 0.08 0.41 0.45 0.3 Plot given data Identify two nearest clusters Repeat process until all objects in same cluster Average link Average distance matrix Construct a distance matrix 1 2 3 4 5 1 0 2 0.24 0 3 0.22 0.15 0 4 0.37 0.2 0.15 0 5 0.34 0.14 0.28 0.29 0 6 0.23 0.25 0.11 0.22 0.39 6 0 Divisive Clustering All items are initially placed in one cluster The clusters are repeatedly split in two until all items are in their own cluster 1 A B 2 C E 3 1 D Difficulties in Hierarchical Clustering Difficulties regarding the selection of merge or split points This decision is critical because the further merge or split decisions are based on the newly formed clusters Method does not scale well So hierarchical methods are integrated with other clustering techniques to form multiple-phase clustering Types of hierarchical clustering techniques BIRCH-Balanced Iterative Reducing and Clustering using hierarchies ROCK: Robust clustering with links, explores the concept of links CHAMELEON: hierarchical clustering algorithm using dynamic modeling Outlier Analysis Outliers are data objects, which are different from or inconsistent with the remaining set of data Outliers can be caused because of Measurement or execution error Result of inherent data variability Can be used in fraud detection Outlier detection and analysis is referred to as outlier mining. Applications of outlier mining Fraud detection Customized marketing for identifying the spending behavior of customers with extremely low or high incomes. Medical analysis for finding unusual responses to various medical treatments. What is outlier mining? Given a set of n data points or objects and k, the expected number of outliers find the top k objects that are dissimilar, exceptional or inconsistent with respect to remaining data There are two subproblems Define what data can be considered as inconsistent in a given data set Method to mine the outliers Methods of outlier detection Statistical approach distance-based approach Density-based local outlier approach Deviation-based approach Statistical Distribution Identifies outliers with respect to a discordancy test Discordancy test examines a working hypothesis and an alternative hypothesis It verifies whether an object oi, is significantly large in relation to the distribution F. This helps in accepting the working hypothesis or rejecting it (alternative distribution) Inherent alternative distribution Mixture alternative distribution Slippage alternative distribution Procedures for detecting outliers Block procedures: All suspect objects are treated as outliers or all of then are accepted as consistent Consecutive procedures: object that is least likely to be an outlier is tested first. If it is found to be an outlier then all of the more extreme values are also considered as outliers. Else the next most extreme object is tested and so on Questions in Clustering