* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Technical Drawings
Survey
Document related concepts
Transcript
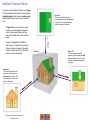
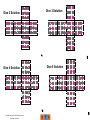
First Class Technical Drawing Class Objectives •Explain the syllabus, grading and attendance policy. •Explain the terminology of technical drawings •Explain the concept of multiview drawing as it applies to simple objects. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Note: It is the student's responsibility to inform the instructor when circumstances prevent him/her from attending class. When a student believes that their absence qualifies as an excused absence, they should contact the instructor (preferably by email) and request that the absence be excused and offer a reason(s) why they believe an excused absence is warranted. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Examples of How Drawings are Graded: What the student submitted: Minus 5-Mistakes that would result in the part being manufactured incorrectly (things that change the design intent) or leaving off information necessary to manufacture the part. -omitting a required dimension -incorrectly noting a dimension value -features that are not drawn or modeled to their true size -features that are located incorrectly -omitting visible line(s) of a feature -omitting notation required to manufacture part (example: not specifying a material, or specifying the wrong material). -incorrect placement or orientation of multiviews (example: placing a top view below a front view). -failure to display parentheses around a reference dimension Minus 3 – Mistakes affecting the precision of the part at manufacture (maximum of 5 points if numerous similar errors-incorrect precision noted on dimension (example: dimension should read 2.000 but is shown on drawing as 2.00) -rounding error on a dimension (example: dimension should read 1.875 but is shown on drawing as 1.88 Minus 2 – Mistakes that create problems for manufacturers -omitting or improperly noting scale of drawing in title block -omitting hidden or center line(s), -lines projected incorrectly from one view to the next but not involving an incorrect dimension -part number in detail drawing does not match part number in balloon and/or parts list -printing in color when monochrome is specified (or other printing error). Minus 1-Minor Mistakes -misspelled words -capitalization mistake(s) -LTscale problems (example: no gaps showing in center-lines (-2 max for multiple instances) -incorrect text height (-2 max for multiple instances of a specific mistake) -incorrect placement of dimensions (-2 max for multiple instances of a same mistake) -incorrect dimension spacing (-2 max for multiple instances of a same mistake) -improper dimension style settings (-2 max for multiple instances of a same mistake) -incorrect line weight, etc. (-2 max for multiple instances of a same mistake) -not dimensioning a cylinder on its side view -no date shown in title block -incorrect sheet numbering, drawing number, or drawing name -incorrect formatting of notes (example: notes that are not numbered, or text height of notes does not match dimension text height) What the instructor handed back: © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt 10% OFF EACH DAY AN ASSIGNMENT IS LATE AND IS NOT ACCEPTED AFTER 3 DAYS © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Architectural CAD Degree Plan © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Civil CAD Degree Plan © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Mechanical CAD Degree Plan © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Electronic CAD Degree Plan © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Interdisciplinary CAD Degree Plan © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Certificate Plans at ACC Certificate Programs in Architectural and Engineering Computer Aided Design of vary in length. Four Areas of emphasis to choose from: -General Certificate (36 Hours) -Integrated Circuit Layout and Design (27 Hours) -Civil (16 Hours) -CAD Management (12 Hours) Many students complete the Certificate requirements while fulfilling the requirements of the Associate Degree. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt CAD Certificate Plans © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Today’s Lesson-Part 1: Technical Drawings Introduction Technical Drawings are the graphics and documentation (notes and specifications) used by manufacturers to fabricate electronic and mechanical products, and by construction professionals to produce architectural structures (houses and buildings) and civil engineering projects (roads, dams, bridges). Other terms often used to describe the creation of technical drawings are: drafting, engineering graphics, engineering drawings, and CAD (Computer Aided Design). Technical drawing is not a new concept, there is archeological evidence suggesting that humans first began creating crude technical drawings several thousand years ago. Through the ages, architects and designers, including Leonardo Da Vinci, created technical drawings. But a French mathematician named Gaspard Monge is considered by many to be the founder of modern technical drawing. Monge’s thoughts on the subject, Geometrie Descriptive (Descriptive Geometry), published around 1799 became the basis for the first university courses. The first English-language text on technical drawing, Treatise on Descriptive Geometry, was published in 1821 by Claude Crozet, a professor at the United States Military Academy. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Chapter 2. Part 1- The Language and Terminology of Technical Drawing Chapter Objectives - at the completion of this chapter students will be able to: •Define the terminology used to describe the geometry of multiview drawings •Describe points, lines, angles •Describe polygons •Describe 3D objects •Describe projection planes •Describe normal, inclined and oblique surfaces •Describe line types •Describe line weights •Interpret the multiviews of graphic primitives •Describe orthographic projection including the miter line technique © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Points, Planes, and Lines Points A point is an exact “location” in space that is defined by coordinates that are located relative to a known origin point. Points are often represented in technical drawings by a visible “dot”, and while the dot representing a point is visible, the point has no dimensional size. Locating Points in Two Dimensional (2D) Coordinate Systems In a two dimensional (2D) coordinate system, points are defined on a 2D flat surface that represents a plane. The coordinates of the point are located by measuring from two perpendicular lines that represent the X (horizontal) and Y (vertical) axes. The intersection where the X and Y axes meet is called the origin. In technical drawings, the X and Y axes represent a 2D area referred to as the “XY plane”. In the example below, the origin point’s value would be stated as “zero comma zero”, or (0,0), which means the location of the origin is zero units (0) on the X axis and zero units (0) on the Y axis. A point, represented by a green dot, is located at coordinate 2,3. This means that the point’s location is 2 units to the right of the origin on the X axis and 3 units above the origin on the Y axis. Point located at 2,3 Note: Coordinates that are defined relative to a 0,0 origin are also referred to as absolute coordinates. Origin (0,0) © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt In the example below, two points (in red) are defined on the XY plane at coordinates 1,2 and 4,3 respectively. Origin Point (0,0) Points that lie on the same plane are referred to as coplanar. Points that share the same location are referred to as coincident. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Negative Values in Two Dimensional (2D) Coordinate Systems Points that are located below the X axis, or to the left of the Y axis, are described with negative coordinate values (a minus sign precedes the coordinate). In the example below, two points are defined at coordinates -3,1 and -1.5,-2.5 respectively. Origin Point (0,0) © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Three Dimensional (3D) Coordinate Systems In a three dimensional (3D) coordinate system, a Z axis is added to the X and Y axes. Using this system, points can be located relative to the origin along the X, Y and Z axes. The Z axis represents the height of the point above or below the X,Y plane (see figure below). For example, a 3D coordinate might be defined with the coordinates 1,1,1. This coordinate would lie one unit to the right of the origin along the X axis, one unit from the origin along the Y axis, and one unit above the X,Y plane. Origin Point (0,0,0) of a 3D coordinate system © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Lines To a mathematician, a line is a set of continuous points that extend indefinitely in either direction. In technical drawing terminology, a line is a segment defined by two endpoints. The endpoints are defined with coordinates. Points that lie on the same line are referred to as collinear. Noncollinear points do not lie on the same line. In the example below, a red line begins at a start point located at coordinate 2,2 and ends at a point located at coordinate 8,7 (relative to the origin). These point are collinear. A point located exactly halfway between the start and end points would be the line’s midpoint. Parallel Lines Parallel lines run side by side at a uniform distance and never intersect, even if extended. Two or more planes can be parallel relative to each other. Lines can be parallel to planes. Spline A smooth curve that passes through, or near, specified points. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Angles Angle An angle is formed when two, noncollinear lines have the same endpoint. The angle at right is formed by sides BA and BC. The angle formed by these lines is referred to as angle ABC. Vertex In 2D space, the common point where two lines meet is called a vertex. The plural of vertex is vertices. In the example at right, angle ABC’s vertex is point B and the its sides are lines BA and BC. Note: When specifying an angle using letters or numbers, the vertex should be the middle letter in the series. Note: The point where two lines cross is referred to as an intersection - as opposed to a vertex. In 3D objects, a vertex is where the object’s edges meet. In the object at right, all of the vertices have been assigned a number. This object has a total of 17 vertices. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Types of Angles Right Angle Acute Angle Obtuse Angle The angle between the sides measures exactly 90 degrees. The angle between the sides measures less than 90 degrees. The angle between the sides measures greater than 90 degrees but less than 180 degrees. Perpendicularity When two lines meet to form a right angle, they are perpendicular. In the example above, line BA is perpendicular to line BC. Planes that meet at right angles to each other are considered to be perpendicular (see example at right), Lines can also be perpendicular to planes. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Types of Angles Complementary Angles If two angles have a total measurement of 90 degrees they are complementary angles. Supplementary Angles If two angles have a total measurement of 180 degrees they are supplementary angles. Opposite Angles Adjacent Angles When two lines cross, they form 4 angles. The opposite angles have the same measure. Where two lines cross, angles that share a common side and common vertex, are called adjacent angles. The sum of any two adjacent angle equals 180 degrees. Therefore: Angle A = Angle B and Angle C = Angle D Therefore, Angles A + C = 180 degrees and Angle C + B = 180 degrees, Angle B + D = 180 degrees and Angle D + A = 180 degrees. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Circles Tangent Circles When a line touches a circle at only one point. A circle can be defined by its center point and either a diameter or radius (diameter/2) Tangency Point Diameter Symbol Radius Center Point Two circles that touch at only one point are tangent. Flat surfaces can also be tangent to curved surfaces. Concentricity When two or more circles share a common center point they are concentric. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Eccentricity When two or more circles do not share a common center point they are eccentric. Polygons Polygons are multi-sided, 2D figures composed of straight line segments. The polygon’s start and end points meet at the same point which creates a “closed” figure. Polygons are classified by the number of sides they contain. Triangles - Three sided polygons. Quadrilaterals - Four sided polygons. Right Triangle Rectangle Square One right angle. Equilateral Three equal angles. Scalene No equal angles. Hexagons - Six sided polygons. Hexagon constructed by inscribing it within a circle. Hexagon constructed by circumscribing it around a circle. Pentagons - Five sided polygons. Heptagon - Seven sided polygons. Octagons - Eight sided polygons. Nonagons - Nine sided polygons. Decagons - Ten sided polygons. Dodecagons - Twelve sided polygons. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Cylinders Cylinders A cylinder is a 3D object that is defined by its center axis, diameter or radius (diameter/2), and height. Flat surfaces can also be tangent to curved surfaces. Plane tangent to a cylinder Center Axis Coaxial When two or more cylinders are aligned along the same center axis they are coaxial. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Center planes meeting along center axis. Today’s Lesson-Part 2: An Introduction to Multiview Drawing Multiview drawing is a technique used by drafters and designers to depict a three-dimensional object as a group of related two-dimensional “views” that show the size and shape of the object. For example, Figure 2.1 provides a three-dimensional (3D) image of a school bus, and while a 3D view of the bus is very helpful in visualizing its overall shape, it doesn’t show the viewer all of the sides of the bus, or the true length, width, or height of the bus. Figure 2.1 A three dimensional image of a school bus. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt A better way to fully describe the bus graphically would be to create a multiview drawing as shown in Figure 2.2. The multiview drawing of the bus is represented by six views, the front, top, sides, back and bottom. These views represent the six “regular” views of the bus. In creating the multi-view drawing of the bus, the front, or principal, view was drawn first. The bus was then “rotated” at 90 degree intervals relative to the front view to create the top, bottom, right and left side views. The left side view was then rotated 90 degrees to the left to create the rear view. Some form of multiview drawing is employed by every discipline of engineering or architecture, so in order to be successful in their careers, drafters and designers must master the techniques involved in creating and interpreting multiview drawings. Top View Figure 2.2 The multiviews of the bus. Rear View Left View Front View Right View Bottom View © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt While a total of six views are possible using the multiview drawing technique, drafters draw only the views necessary to describe an object. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Multiview Projection Planes If a house is placed inside a glass box as in Figure 2.3, the transparent sides of the box would create projection planes (also known as viewing planes) that the features of the house can be “projected” onto. Figure 2.6 The view through the horizontal projection plane shows the top view or roof plan. This view reveals the width and depth of the house. Likewise, in Figures 2.5 and 2.6, the right side and top views of the house are shown as they would appear if projected onto the profile projection and horizontal projection planes respectively. Figure 2.4 The view through the frontal projection plane shows the front view of the house. This view furnishes the width and height of the house. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Viewer’s Line of Sight In Figure 2.4 the front view of the house is shown as it would appear if projected onto a frontal projection plane that has been placed between the viewer and the object. Figure 2.3 Figure 2.5 The view through the profile projection plane reveals the right side view of the house. This view furnishes the depth and height of the house. In Figure 2.7, notice how a feature like the peak of the roof in the front view, is exactly in line with the top of the roof in both the left and right views. Observe how the features of the chimney are depicted in each of the views. The planes representing the roof in the right, left, and top views appear as rectangles in the multiviews, but by studying them in relation to the front view, you will see that they actually represent the sloping planes of the roof. Since the planes of the roof, as projected through the top and side projection planes are sloping, they are not drawn actual, or true size. In technical drawing, this phenomenon is referred to as “foreshortening”. Figure 2.7 The “Elevations” of a House as They would Appear in a Multiview Drawing. TOP VIEW LEFT VIEW © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt FRONT VIEW RIGHT VIEW First Class Activity Creating 2D Multiviews of a 3D Object In this activity your instructor will furnish you with a die. Orient the die so that the front and top views match the ones show at right. Starting from this orientation, rotate the die as needed to find the missing views (right, left, back and bottom). Fill in the circles to match the corresponding view. Repeat this process to complete each of the other sheets. Return the die to your instructor following this activity. © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 1 Solution © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 2: © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 3: © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 4: © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 5: © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Dice 3 Solution Dice 2 Solution 2 3 Dice 5 Solution Dice 4 Solution 4 5 © Technical Drawing 101 with AutoCAD All Rights Reserved Smith, Ramirez and Schmidt Home Work Assignment: Read all of Chapter 1 and up through the Chapter Summary of Chapter 2. Unit 2. Multiview Drawing Chapter Objectives •Explain what multiview drawings are and their importance to the field of technical drawing. •Explain how views are chosen and aligned in a multiview drawing. •Visualize and interpret the multiviews of an object. •Describe the line types and line weights used in technical drawings as defined by the ASME Y14.2M standard. •Explain the difference between drawings created with First Angle and Third Angle projection techniques. •Use a miter line to project information between top and side views. •Create multiview sketches of objects including the correct placement and depiction of visible, hidden and center lines. © Technical Drawing 101 with AutoCAD Smith, Ramirez and Schmidt