* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 6/11 Erwin Sitompul University Physics: Mechanics
Relativistic mechanics wikipedia , lookup
Center of mass wikipedia , lookup
Analytical mechanics wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Jerk (physics) wikipedia , lookup
Fictitious force wikipedia , lookup
Statistical mechanics wikipedia , lookup
Mass versus weight wikipedia , lookup
Fundamental interaction wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Equations of motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Centripetal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Rigid body dynamics wikipedia , lookup
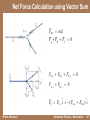
Lecture 6 Ch5. Newton’s Law of Motion University Physics: Mechanics Dr.-Ing. Erwin Sitompul http://zitompul.wordpress.com Announcement Next week 1st half : Lecture 7 2nd half : Quiz 2 Material: Lecture 5 & 6 Over next week 1st half : Lecture 8, Make-up Quiz 2 2nd half : Discussion Quiz 2 Erwin Sitompul University Physics: Mechanics 6/2 What Causes an Acceleration? Out of common experience, we know that any change in velocity must be due to an interaction between an object (a body) and something in its surroundings. An interaction that can cause an acceleration of a body is called a force. Force can be loosely defined as a push or pull on the body. The relation between a force and the acceleration it causes was first understood by Isaac Newton. The study of that relationship is called Newtonian mechanics. We shall now focus on its three primary laws of motion. Sir Isaac Newton (1642—1727) Erwin Sitompul University Physics: Mechanics 6/3 Newton’s First Law Newton’s First Law: “If no force acts on a body, then the body’s velocity cannot change, that is the body cannot accelerate.” In other words, if the body is at rest, it stays at rest. If the body is moving, it will continue to move with the same velocity (same magnitude and same direction). Erwin Sitompul University Physics: Mechanics 6/4 Force A force can cause the acceleration of a body. As the standard body, we shall use the standard kilogram. It is assigned, exactly and by definition, a mass of 1 kg. We put the standard body on a horizontal frictionless surface and pull the body to the right, so that it eventually experiences an acceleration of 1 m/s2. We can now declare, as a matter of definition, that the force we are exerting on the standard body has a magnitude of 1 newton (1 N). Erwin Sitompul University Physics: Mechanics 6/5 Force Forces are vector quantities. They have magnitudes and directions. Principle of Superposition for Forces: A single force with the magnitude and direction of the net force acting on a body has the same effect as all the individual forces acting together. Newton’s First Law: (proper statement) → “If no net force acts on a body (Fnet = 0), then the body’s velocity cannot change, that is the body cannot accelerate.” Erwin Sitompul University Physics: Mechanics 6/6 Net Force Calculation using Vector Sum Fnet m a FA FB FC 0 FA, x FB , x FC , x 0 FA, y FB , y 0 FC FC , x ˆi ( FA, x FB , x ) ˆi Erwin Sitompul University Physics: Mechanics 6/7 Checkpoint Which of the following six→arrangements correctly show the → vector addition of forces F1 and F2 to yield the → third vector, which is meant to represent their net force Fnet? Erwin Sitompul University Physics: Mechanics 6/8 Mass Mass is a scalar quantity. Mass is an intrinsic characteristic of a body. The mass of a body is the characteristic that relates a force on the body to the resulting acceleration. A physical sensation of a mass can only be obtained when we attempt to accelerate the body. Erwin Sitompul University Physics: Mechanics 6/9 Newton’s Second Law Newton’s Second Law: “The net force on a body is equal to the product of the body’s mass and its acceleration.” The Newton’s second law in equation form F net ma → force F → net It the net on a body is zero, then the body’s acceleration a is zero If the body is at rest, it stays at rest. If it is moving, it continues to move at constant velocity. 1 N (1 kg)(1 m s 2 ) 1 kg m s Erwin Sitompul 2 University Physics: Mechanics 6/10 Newton’s Second Law → The vector equation Fnet = ma is equivalent to three component equation, one written for each axis of an xyz coordinate system: Fnet,z maz . Fnet,x max , Fnet,y ma y , The acceleration component along a given axis is caused only by the sum of the force components along that same axis, and not by force components along any other axis. Erwin Sitompul University Physics: Mechanics 6/11 Free-Body Diagram The most important step in solving problems involving Newton’s Laws is to draw the free-body diagram. Only the forces acting on the object of interest should be included in a free-body diagram. Fon book from hand Fon book from earth Erwin Sitompul University Physics: Mechanics 6/12 Free-Body Diagram The system of interest is the cart The free-body diagram of the cart Erwin Sitompul University Physics: Mechanics 6/13 Example: Puck (Ice Hockey “Ball”) Three situations in which one or two forces act on a puck that moves over frictionless ice along an x axis, in one-dimensional motion, are presented here. → → The puck’s mass is m = 0.2 kg. Forces F1 and F2 are directed along the → axis and have magnitudes F1 = 4 N and F2 = 2 N. Force F3 is directed at angle θ = 30° and has magnitude F3 = 1 N. In each situation, what is the acceleration of the puck? F1 max F1 4N ax 20 m s2 m 0.2 kg Erwin Sitompul University Physics: Mechanics 6/14 Example: Puck (Ice Hockey “Ball”) The puck’s mass is m = 0.2 kg. Forces F1 and F2 are directed along the axis and have magnitudes F1 = 4 N and F2 = 2 N. Force F3 is directed at angle θ = 30° and has magnitude F3 = 1 N. F3,x F2 max ax F1 F2 max 4 N2 N ax 0.2 kg 10 m s 2 Erwin Sitompul F3,x F2 m F3 cos F2 m (1 N)(cos30) 2 N 0.2 kg 5.67 m s2 University Physics: Mechanics 6/15 Some Particular Forces The Gravitational Force → The gravitational force Fg on a body is a force that pulls on the body, directly toward the center of Earth (that is, directly down toward the ground. F g mg Fg mg The Weight The weight W of a body is equal to the magnitude Fg of the gravitational force on the body W mg Erwin Sitompul University Physics: Mechanics 6/16 Some Particular Forces The Normal Force When a body presses against a surface, the surface (even a seemingly rigid one)→deforms and pushes back on the body with a normal force FN that is perpendicular to the surface. In mathematics, normal means perpendicular. According to Newton’s second law, FN FN FN Fg ma y FN mg m(0) FN mg • Why? Forces on a Body, Resting on a Table Erwin Sitompul University Physics: Mechanics 6/17 Some Particular Forces Friction → The frictional force or simply friction is a force f that resists the motion when we slide or attempt to slide a body over a surface. Friction is directed along the surface, opposite the direction of the intended motion. Erwin Sitompul University Physics: Mechanics 6/18 Some Particular Forces Tension When a cord (or a rope, cable, or other such object) is attached→to a body and tensed, the cord pulls on the body with a force T directed away from the body. The force is often called → a tension force. The tension in the cord is the magnitude T of the force on the body. • A cord is considered as massless and unstretchable • A pulley is considered as massless and frictionless Erwin Sitompul University Physics: Mechanics 6/19 Beware of High Energy Concentration Erwin Sitompul University Physics: Mechanics 6/20 Forms of Energy Erwin Sitompul University Physics: Mechanics 6/21 Newton’s Third Law Newton’s Third Law: “When two bodies interact, the forces on the bodies from each other are always equal in magnitude an opposite in direction.” FBC FCB (Equal Magnitudes) FBC FCB (Equal Magnitudes and Opposite Directions) FBC : The force on the book B from the box C FCB : The force on the box C from the book B Erwin Sitompul University Physics: Mechanics 6/22 Applying Newton’s Law: Problem 1 A block S (the sliding block) with mass M =3.3 kg is free to move along a horizontal frictionless surface. It is connected by a cord that wraps over a frictionless pulley, to a second block H (the hanging block) with mass m = 2.1 kg. The cord and pulley are considered to be “massless”. The hanging block H falls as the sliding block S accelerate to the right. Find: (a) the acceleration of block S (b) the acceleration of block H (c) the tension in the cord Erwin Sitompul University Physics: Mechanics 6/23 Applying Newton’s Law: Problem 1 FN FN The Forces Acting On The Two Blocks Erwin Sitompul Free-Body Diagram for Block S and Block H University Physics: Mechanics 6/24 Applying Newton’s Law: Problem 1 Fnet,x Max T Max FN The cord does not stretch, so ax of M and ay of m have the same magnitude. ax of M ay of m a 2 Fnet,y Ma y FN Fg S 0 FN Fg S The tension at M and the tension at m also have the same magnitude. 1 T FgH ma T mg ma • Why? 2 Ma mg ma Fnet,y ma y T FgH ma y a m g M m 1 Erwin Sitompul University Physics: Mechanics 6/25 Applying Newton’s Law: Problem 1 a m 2.1 g 9.8 3.81m s 2 M m 3.3 2.1 (a) the acceleration of block S aS 3.81iˆ m s2 (b) the acceleration of block H aH 3.81jˆ m s 2 (c) the tension in the cord T Ma (3.3)(3.81) 12.573 N Erwin Sitompul University Physics: Mechanics 6/26 Applying Newton’s Law: Problem 2 A cord pulls on a box of sea biscuits up along a frictionless plane inclined at θ = 30°. The box has mass m = 5 kg, and the force from the cord has magnitude T = 25 N. What is the box’s acceleration component a along the inclined plane? Free-Body Diagram of the Box Erwin Sitompul Free-Body Diagram, → Fg in components University Physics: Mechanics 6/27 Applying Newton’s Law: Problem 2 Fnet,x max T mg sin max T mg sin ax m 25 (5)(9.8) sin 30 5 2 0.1 m s • What is the meaning of this value? What is the force exerted by the plane on the box? Fnet,y ma y FN mg cos ma y No motion in FN mg cos m(0) • y direction FN mg cos (5)(9.8) cos 30 42.435 N Erwin Sitompul University Physics: Mechanics 6/28 Homework 5: Two Boxes and A Pulley A block of mass m1 = 3.7 kg on a frictionless plane inclined at angle θ = 30° is connected by a cord over a massless, frictionless pulley to a second block of mass m2 = 2.3 kg. What are: (a) the magnitude of the acceleration of each block, (b) the direction of the acceleration of the hanging block, and (c) the tension in the cord? Hint: Draw the free-body diagram of m1 and m2 first. Erwin Sitompul University Physics: Mechanics 6/29