Download Energy and Electrostatics - Appoquinimink High School

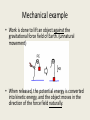
Energy and Electrostatics
A new definition of potential energy
• An object has potential energy due to its
location within a force field.
• To change the object’s location (and therefore
potential energy), work has to be done by
applying a force on the object.
Mechanical example
• Work is done to lift an object against the
gravitational force field of Earth. (unnatural
movement)
• When released, the potential energy is converted
into kinetic energy, and the object moves in the
direction of the force field naturally.
Electric potential energy
• A charged object has PE due to its location
within an electric field.
• Work is required to move a charged object
against the electric field. When released, that
PE will be converted into KE naturally in the
direction of the field.
Guiding questions
• Answer questions #1 - #5 now please.
Electric Potential
• In electricity, rather than deal with total PE, it
is more convenient to deal with electric
potential energy per charge since there could
be many charges in the field (think a circuit)
• We call this electric potential for short
– Measured in Volts, and symbolized with a “V”
electric _ potential _ energy
V
ch arg e _ in _ field
Electric potential
• Rearranging the previous equation, we get…
• W = qV
• When we get to circuits, this will be useful
because if we are using a 9V battery, the
amount of work we get out of a charge
moving through the circuit will be 9V*charge.
More about Volts
• 1 volt = 1 joule of energy per coulomb of
charge
• Example, if a conductor has a potential of
1000 volts, it would take 1000 joules of energy
per coulomb to bring a small charge from far
away and add it to the charge of the
conductor.
Guiding questions
• Answer #6 now please
Current
The movement of electrons through a
conductor. The rate at which charge flows.
charge
current 
time
I=
q
t
Coulombs
units:
= Ampere = Amp = A
Second
DC (Direct Current) – All charges move in one direction in the
circuit.
AC (Alternating Current) – charges move one way and then the
other, changing direction from moment to moment.
CIRCUIT:
A path where electrons flow
and their energy is used.
RESISTANCE:
Opposition to the flow of
electrons in a circuit.
THE DAM ANALOGY
Dam = Battery, Outlet,
Power Supply
Water Depth =
V = Voltage or Potential
Pipe =
Wire
Water Wheel =
Energy
User/Converter
(Light Bulb, Motor…)
Valve = Resistance or Current Control
GROUND or Lowest Potential
How can the resistance change?
• What are the variables that effect the
resistance of the flow of the water in the Dam
Analogy?
• Resistance is much like friction. The more
“friction” against a current, the more
resistance.
First variable
• What would happen if we widen the
path for the water?
• The resistance would be less.
• Therefore: R is in proportion to 1/A
2nd variable
• What would happen if we shorten the path of
the valve?
• There would be less to flow through, therefore
the resistance would be less.
• Therefore, R is proportional to L
3rd variable
• What would happen if we thicken the walls of
the pathway for the water?
• There would be more resistance.
• Therefore, R is proportional to density of the
material.
4th variable
• What would happen if we heat up the
pathway of the water?
• The resistance would increase
• As resistance goes up, temperature goes up.
Summary
•
1)
2)
3)
4)
Resistance of an object depends on
Cross-sectional area of the resistor
Length of the resistor
Density of the resistor
Temperature of the resistor
Guiding questions
• Answer #7 now please
What does the dam analogy tell us about
the relationship between I and R?
As R increases, I ……
DECREASES!
or
How could the current be increased in a
circuit whose resistance is held constant?
Increase the “push” or VOLTAGE
Georg Simon Ohm
Ohm’s Law:
V
Voltage
I  UNITS FOR
Current 
RESISTANCE
Resistance
R
Volts
Can Be Written As:

Ohm


More Typically Written As:
Amp
V
V

IR
R
This tells you the number of volts necessary
to push 1
amp of current through the device.
I
OR
Power
• Deriving power of a circuit
• P = Work/time
• How is work related to potential of a circuit?
Guiding questions
• Answer #8 now please.