* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download lec15 - UConn Physics
Survey
Document related concepts
Transcript
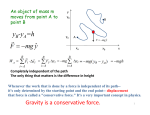
Today’s Topics Potential Energy, Ch. 8-1 Conservative Forces, Ch. 8-2 Conservation of mechanical energy Ch.8-4 Physics 151: Lecture 15, Pg 1 New Topic - Potential Energy Consider a ball at some height above the ground. No Velocity Some Velocity Physics 151: Lecture 15, Pg 2 New Topic - Potential Energy Consider a ball at some height above the ground. What work is done in this process ? (Work done by the earth on the ball) h W = F. Dx W = mgh cos(0) W = mgh Physics 151: Lecture 15, Pg 3 New Topic - Potential Energy Consider a ball at some height above the ground. h Before the ball falls it has the potential to do an amount of work mgh. We say the ball has a potential energy of U = mgh. By falling the ball loses its potential energy, work is done on the ball, and it gains some kinetic energy, W = DK = 1/2 mv2 = -DU = mgh Physics 151: Lecture 15, Pg 4 Lecture 15, ACT 1 Work Done by Gravity The air track is at an angle of 30 degrees with respect to horizontal. The cart (with mass 1 kg) is released. It bounces back and forth on the track. It falls 1 meter down the track, then bounces back up to its original position. How much total work is done by gravity on the cart when it reaches its original position. 30 degrees A) 5 J B) 10 J C) 20 J D) 0 J Physics 151: Lecture 15, Pg 5 Some Definitions Conservative Forces - those forces for which the work done does not depend on the path taken, but only the initial and final position. Potential Energy - describes the amount of work that can potentially be done by one object on another under the influence of a conservative force W = -DU only differences in potential energy matter. Physics 151: Lecture 15, Pg 6 See text: 8.1 Potential Energy For any conservative force F we can define a potential energy function U in the following way: W = F.dr = - DU The work done by a conservative force is equal and opposite to the change in the potential energy function. r2 U2 This can be written as: F.dr r2 DU = U2 - U1 = - W = - r1 r1 U1 Physics 151: Lecture 15, Pg 7 Question - 1 For a force to be a conservative force, when applied to a single test body: a. it must have the same value at all points in space. b. it must have the same direction at all points in space. c. it must be parallel to a displacement in any direction. d. equal work must be done in equal displacements. e. no work must be done for motion in closed paths. Physics 151: Lecture 15, Pg 8 See text: 8-1 A Conservative Force : Spring For a spring we know that Fx = -kx. F(x) x1 x2 x relaxed position -kx F = - k x1 F = - k x2 See Figure 7-7 Physics 151: Lecture 15, Pg 9 See text: 8-1 Spring... The work done by the spring Ws during a displacement from x1 to x2 is the area under the F(x) vs x plot between x x1 and x2. 2 Ws F ( x)dx x1 x2 F(x) x1 ( kx)dx x2 x1 x Ws -kx 1 2 x kx x 2 1 Ws k x22 x12 2 2 1 1 U Ws k x22 x12 2 See Figure 7-7 Physics 151: Lecture 15, Pg 10 Question - 2 The force a spring exerts on a body is a conservative force because : 1. a spring always exerts a force opposite to the displacement of the body. the work a spring does on a body is equal for compressions and extensions of equal magnitude. the work a spring does on a body is equal and opposite for compressions and extensions of equal magnitude. the net work a spring does on a body is zero when the body returns to its initial position. 2. 3. 4. Physics 151: Lecture 15, Pg 11 Lecture 15, ACT 2 Work/Energy for Conservative Forces The air track is is again at an angle of 30 degrees with respect to horizontal. The cart (with mass 1 kg) is released 1 meter from the bottom and hits the bumper with some speed, v1. You want the cart to go faster, so you release the cart higher. How high do you have to release the cart so it hits the bumper with speed v2 = 2v1? 30 degrees A) 1 m B) 2 m C) 4 m D) 8 m Physics 151: Lecture 15, Pg 12 See text: 8-4 Conservation of Energy If only conservative forces are present, the total energy (sum of potential and kinetic energies) of a system is conserved. E=K+U DE = DK + DU = W + DU = W + (-W) = 0 E = K + U is constant !!! using DK = W using DU = -W Animation_2 Animation_3 Both K and U can change, but E = K + U remains constant. Physics 151: Lecture 15, Pg 13 ACT - 3 A 0.04-kg ball is thrown from the top of a 30-m tall building (point A) at an unknown angle above the horizontal. As shown in the figure, the ball attains a maximum height of 10 m above the top of the building before striking the ground at point B. If air resistance is negligible, what is the value of the kinetic energy of the ball at B minus the kinetic energy of the ball at A (KB – KA)? Animation_1 a. 12 J b. –12 J c. 20 J d. –20 J e. 32 J Physics 151: Lecture 15, Pg 14 Lecture 16, Example Skateboard What speed will skateboarder reach at bottom of the hill ? .. Conservation of Total Energy: m = 25 kg v ~ 8 m/s (~16mph) ! Does NOT depend on the mass ! R=3 m .. Physics 151: Lecture 15, Pg 15 Lecture 16, Example Skateboard What would be the speed if instead the skateboarder jumps to the ground on the other side ? .. KINEMATICS: R=3 m .. the same magnitude as before ! and independent of mass Physics 151: Lecture 15, Pg 16 A Non-Conservative Force Friction Looking down on an air-hockey table with no air, Path 2 Path 1 For which path does friction do more work ? Physics 151: Lecture 15, Pg 17 A Non-Conservative Force Path 2 Since |W2|>|W1| the puck will be traveling slower at the end of path 2. Work done by a nonconservative force takes energy out of the system. Path 1 W1 = -mmg d1 W2 = -mmg d2 since d2 > d1, -W2 > -W1 Physics 151: Lecture 15, Pg 18 Lecture 15, ACT 4 Work/Energy for Non-Conservative Forces The air track is is again at an angle of 30 degrees with respect to horizontal. The cart (with mass 1 kg) is released 1 meter from the bottom and hits the bumper with some speed, v1. This time the vacuum/ air generator breaks half-way through and the air stops. The cart only bounces up half as high as where it started. How much work did friction do on the cart ? 30 degrees A) 2.5 J B) 5 J C) 10 J D) –2.5 J E) –5 J F) –10 J Physics 151: Lecture 15, Pg 19 Generalized Work Energy Theorem: Suppose FNET = FC + FNC (sum of conservative and nonconservative forces). The total work done is: WTOT = WC + WNC The Work Kinetic-Energy theorem says that: WTOT = DK. WTOT = WC + WNC = DK WNC = DK - WC But WC = -DU So WNC = DK + DU = DE Physics 151: Lecture 15, Pg 20 Example - 2 A 12-kg block on a horizontal frictionless surface is attached to a light spring (force constant = 0.80 kN/m). The block is initially at rest at its equilibrium position when a force (magnitude P = 80 N) acting parallel to the surface is applied to the block, as shown. What is the speed of the block when it is 13 cm from its equilibrium position? k v1= 0 F m v2=? 0.78 m/s x Physics 151: Lecture 15, Pg 21 Question 1. 2. 3. 4. 5. As an object moves from point A to point B only two forces act on it: one force is nonconservative and does –30 J of work, the other force is conservative and does +50 J of work. Between A and B, the kinetic energy of object increases, mechanical energy decreases. the kinetic energy of object decreases, mechanical energy decreases. the kinetic energy of object decreases, mechanical energy increases. the kinetic energy of object increases, mechanical energy increases. None of the above. Physics 151: Lecture 15, Pg 22 Question - 2 1. 2. 3. 4. 5. As an object moves from point A to point B only two forces act on it: one force is conservative and does –70 J of work, the other force is nonconservative and does +50 J of work. Between A and B, the kinetic energy of object increases, mechanical energy increases. the kinetic energy of object decreases, mechanical energy increases. the kinetic energy of object decreases, mechanical energy decreases. the kinetic energy of object increases, mechanical energy decreases. None of the above. Physics 151: Lecture 15, Pg 23 ACT- 2 Objects A and B, of mass M and 2M respectively, are each pushed a distance d straight up an inclined plane by a force F parallel to the plane. The coefficient of kinetic friction between each mass and the plane has the same value . At the highest point, 1. 2. 3. 4. KA>KB. KA=KB. KA<KB. The work done by F on A is greater than the work done on B. 5. The work done by F on A is less than the work done on B. Physics 151: Lecture 15, Pg 24 Recap of today’s lecture Conservative Forces and Potential Energy W = -DU Conservation of mechanical energy Physics 151: Lecture 15, Pg 25 Lecture 16, Example Skateboard .. Let’s now suppose that the surface is not frictionless and the same skateboarder reach the speed of 7.0 m/s at bottom of the hill. What was the work done by friction on the skateboarder ? Conservation of W + K + U = K + U 1 1 2 2 f Total Energy : m = 25 kg Wf + 0 + mgR = 1/2mv2 + 0 Wf = 1/2mv 2 - mgR R=3 m .. Wf = (1/2 x25 kg x (7.0 m/s2)2 - 25 kg x 10m/s2 3 m) Wf = 613 - 735 J = - 122 J Total mechanical energy decreased by 122 J ! Physics 151: Lecture 15, Pg 26