Download Common Core Math III Unit 1: STATISTICS!

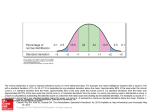
Common Core Math III
Unit 1: Statistics
We will discuss the following four
topics during this unit:
1. Normal Distributions
2. Sampling and Study Design
3. Estimating Population Parameters
4. Expected Value and Fair Game
Characteristics of Normal Distribution
• symmetric with respect to the mean
• mean = median = mode
• 100% of the data fits under the curve
Some New Symbols
parameter
statistic
mean
µ
x
proportion
p
p̂
standard
deviation
σ
s
The Normal Distribution Curve
σ=1
µ=0
-3
-2
-1
0
1
2
3
Z-Score
The z-score is number of standard
deviations (σ) a value is from the mean
(µ) on the normal distribution curve.
What is the z-score of the
value indicated on the curve?
-3
-2
-1
0
1
2
3
What is the z-score of the
value indicated on the curve?
-3
-2
-1
0
1
2
3
Instead of estimating, we are given a
formula to help us find a precise z-score:
What is the meaning of a positive z-score?
What about a negative z-score?
How do you use this?
The mean score on the SAT is 1500,
with a standard deviation of 240. The
ACT, a different college entrance
examination, has a mean score of 21
with a standard deviation of 6.
If Bobby scored 1740 on the SAT and
Kathy scored 30 on the ACT, who
scored higher?
Bobby
z=1
Kathy
z = 1.5
Kathy scored higher.
Kathy’s z-score shows that she scored 1.5
standard deviations above the mean.
Bobby only scored 1 standard deviation above
the mean.
The Empirical Rule
In statistics, the 68–95–99.7 rule, also
known as the empirical rule, states
that nearly all values lie within three
standard deviations of the mean in a
normal distribution.
68% of the data falls within ± 1σ
68%
95% of the data falls within ± 2σ
95%
99.7% of the data falls within ± 3σ
99.7%
When you break it up…
34%
.15%
13.5%
2.35%
34%
.15%
13.5%
2.35%
How do you use this?
The scores on the CCM3 midterm were
normally distributed. The mean is 82 with
a standard deviation of 5. Create and label
a normal distribution curve to model the
scenario.
Draw the curve, add the mean, then add the
standard deviations above and below the mean.
34%
.15%
34%
13.5%
2.35%
67
72
.15%
13.5%
2.35%
77
82
87
92
97
Find the probability that a randomly
selected person:
a. scored between 77 and 87 68%
b. scored between 82 and 87 34%
c. scored between 72 and 87 81.5%
d. scored higher than 92 2.5%
e. scored less than 77
16%
You might be wondering…
what happens if you’re looking
for scores that are not perfect
standard deviations away from
the mean?
normalcdf (lower bound,
upper bound, µ, σ)
a. What’s the probability that a randomly
selected student scored between 80 and 90?
normalcdf (80, 90, 82, 5) = 0.6006
b. What’s the probability that a randomly
selected student scored below 70?
normalcdf (0, 70, 82, 5) = 0.0082
c. What’s the probability that a randomly
selected student scored above 79?
normalcdf (79, 100, 82, 5) = 0.7256
You can also work backward to find percentiles!
d. What score would
a student need in
order to be in the 90th
percentile?
invnorm (percent of area to left, , )
invnorm (0.9, 82, 5) = 88.41, or 89
e. What score would a student need in order
to be in top 20% of the class?
invnorm (0.8, 82, 5) = 86.21, or 87
The average waiting time at Walgreen’s drivethrough window is 7.6 minutes, with a
standard deviation of 2.6 minutes. When a
customer arrives at Walgreen’s, find the
probability that he will have to wait
a. between 4 and 6 minutes 0.186
b. less than 3 minutes 0.037
c. more than 8 minutes 0.439
d. Only 8% of customers have to wait longer
than Mrs. Jones. Determine how long Mrs.
Jones has to wait. 11.25 minutes
Questions
about normal
distribution?
Sampling
and
Study
Design
Main Questions
What’s the difference between an experiment
and an observational study?
What are the different ways that a sample
can be collected?
When is a sample considered random?
What is bias and how does it affect the data
you collect?
There are three ways to collect data:
1. Surveys
2. Observational
Studies
3. Experiments
Surveys
Surveys most often
involve the use of a
questionnaire to
measure the
characteristics and/or attitudes of people.
ex. asking students their opinion about
extending the school day
Observational Studies
Individuals are
observed and
certain outcomes
are measured, but
no attempt is made
to affect the
outcome.
Experiments
Treatments are imposed
prior to observation.
Experiments are the
only way to show a
cause-and-effect
relationship.
Remember:
Correlation is not causation!
Observational Study or Experiment?
Fifty people with clinical depression were
divided into two groups. Over a 6 month
period, one group was given a traditional
treatment for depression while the other group
was given a new drug. The people were
evaluated at the end of the period to determine
whether their depression had improved.
Experiment
Observational Study or Experiment?
To determine whether or not apples really do
keep the doctor away, forty patients at a
doctor’s office were asked to report how often
they came to the doctor and the number of
apples they had eaten recently.
Observational Study
Observational Study or Experiment?
To determine whether music really helped
students’ scores on a test, a teacher who taught
two U. S. History classes played classical music
during testing for one class and played no music
during testing for the other class.
Experiment
Types of Sampling
In order to collect data, we must choose a
sample, or a group that represents the
population.
The goal of a study will determine the type
of sampling that will take place.
Simple Random Sample (SRS)
All individuals in the population have the
same probability of being selected, and all
groups in the sample size have the same
probability of being selected.
Putting 100 kids’
names in a hat and
picking out 10 - SRS
Putting 50 girls’ names
in one hat and 50
boys’ names in
another hat and
picking out 5 of each –
not a SRS
Stratified Random Sample
If a researcher wants to highlight specific
subgroups within the population, they divide
the entire population into different subgroups,
or strata, and then randomly selects the final
subjects proportionally from the different
strata.
Systematic Random Sample
The researcher selects a number at random,
n, and then selects every nth individual for
the study.
Convenience Sample
Subjects are taken from a group that is
conveniently accessible to a researcher, for
example, picking the first 100 people to
enter the movies on Friday night.
Cluster Sample
The entire population is divided into groups,
or clusters, and a random sample of these
clusters are selected. All individuals in the
selected clusters are included in the sample.
Name that sample!
The names of 70 contestants are written on
70 cards, the cards are placed in a bag, the
bag is shaken, and three names are picked
from the bag.
Simple random sample
Convenience sample
Stratified sample
Cluster sample
Systematic sample
Name that sample!
To avoid working late, the quality control
manager inspects the last 10 items
produced that day.
Simple random sample Stratified sample
Convenience sample
Cluster sample
Systematic sample
Name that sample!
A researcher for an airline interviews all of
the passengers on five randomly selected
flights.
Simple random sample
Convenience sample
Stratified sample
Cluster sample
Systematic sample
Name that sample!
A researcher randomly selects and interviews
fifty male and fifty female teachers.
Simple random sample
Convenience sample
Stratified sample
Cluster sample
Systematic sample
Name that sample!
Every fifth person boarding a plane is
searched thoroughly.
Simple random sample
Convenience sample
Stratified sample
Cluster sample
Systematic sample
Warm Up Day 4
The average wait time at the drive through of Tasty
World is 3.2 minutes with a standard deviation of 0.4
minutes.
a) About what percent of people wait between 3.2 minutes and 4
minutes?
b) About what percent of people wait for less than 2 minutes?
c) If 124 cars went through the drive through, how many of them
waited longer than 5 minutes?
d) Melanie waited for 3.7 minutes at Tasty World. Patrick went to
Burger Bang instead where he had to wait 3.9 minutes. The
average wait time at Burger Bang is 3.7 minutes with a standard
deviation of 0.1 minutes. Who waited longer when compared
to each other?
Types of Bias in Survey Questions
Bias occurs when a sample systematically
favors one outcome.
1. Question Wording Bias
In a survey about Americans’ interest in
soccer, the first 25 people admitted to a high
school soccer game were asked, “How
interested are you in the world’s most
popular sport, soccer?”
2. Undercoverage bias occurs when the sample
is not representative of the population.
3. Response bias occurs when survey
respondents lie or misrepresent themselves.
4. Nonresponse bias occurs when an individual
is chosen to participate, but refuses.
5. Voluntary response bias occurs when people
are asked to call or mail in their opinion.
Name that bias!
On the twelfth anniversary of the
death of Elvis Presley, a Dallas
record company sponsored a
national call-in survey. Listeners of
over 1000 radio stations were asked
to call a 1-900 number (at a charge of $2.50)
to voice an opinion concerning whether or not
Elvis was really dead. It turned out that 56% of
the callers felt Elvis was alive.
Voluntary response bias
Name that bias!
In 1936, Literary Digest magazine conducted the most
extensive public opinion poll in history to date. They
mailed out questionnaires to over 10 million people
whose and addresses they had obtained from
telephone books and vehicle registration lists. More
than 2.4 million people responded, with 57%
indicating that they would vote for Republican Alf
Landon in the upcoming Presidential election.
However, Democrat Franklin Roosevelt won the
election, carrying 63% of the popular vote.
Undercoverage bias
Why is this question biased?
Do you think the city should risk an increase in
pollution by allowing expansion of the Northern
Industrial Park?
Can you rephrase it to
remove the bias?
Why is this question biased?
If you found a wallet with $100 in it on the street,
would you do the honest thing and return it to the
person or would you keep it?
Can you rephrase it to
remove the bias?
Questions about sampling?
Estimating Population Parameters
Vocabulary for this lesson is important!
Parameter
a value that represents a
population
Statistic
a value based on a sample
and used to estimate a
parameter
population
sample
parameter
statistic
mean
µ
x
proportion
p
p̂
standard
deviation
σ
s
Finding a Margin of Error
Margin of error is a
“cushion” around a
statistic
1
ME =
n
n = sample
size
Suppose that 900 American teens were surveyed about their
favorite event of the Winter Olympics. Ski jumping was the
favorite of 20% of those surveyed. This result can be used to
predict the proportion of ALL American teens who favor ski
jumping.
pˆ  0.2
ME  1
, or 0.03
900
0.2  0.03  0.17  0.23
20%  3%  17%  23%
We can confidently state that the true percentage
of American teens who favor ski jumping falls
between 17% and 23%.
What sample size produces
a given margin of error?
If you want your margin of error to be
2%, what size sample will you need?
1
.02 
n
2500
How does sample size
affect margin of error?
If your sample size is 400 and you wish
to cut the margin of error in half, what
will your new sample size be?
1
m
 .05
400
1600
So, if you want half
of .05, we need to
1
solve .025 
n
Simulation
Simulation is a way to
model random events,
so that simulated
outcomes closely match
real-world outcomes.
Why run a simulation?
Some situations may be difficult, time-consuming, or
expensive to analyze. In these situations, simulation
may approximate real-world results while requiring
less time, effort, or money.
Carole and John are playing a dice game.
Carole believes that she can roll six dice and
get each number, one through six, on a single
roll. John knows the probability of this
occurrence is low. He bets Carole that he will
wash her car if she can get the outcome she
wants in twenty tries.
BEFORE YOU START!
You are running 20 trials, so make 20
blanks on your paper. This will keep you
from losing count of how many trials
you’ve run. It also makes recording easy!
__
__ __
__ __ __ __ __ __ __


 __
__ __ __ __ __ __ __ __ __
What is the problem that we are simulating?
Can Carole get one of each number in a roll of
six dice?
What random device will you use to simulate
the problem and how will you use it?
We will use the calculator to generate random
numbers.
Seeding
Since a calculator is a type of computer, it can
never be truly random.
For this reason, we can configure our calculators
to give everyone the same set of “random” data
(so we can all work together!).
The process of calibrating our calculators in this
way is called seeding.
How to seed the calculator:
How will you conduct each trial?
How many trials will you conduct?
I will use the randInt( command in my calculator to
generate random integers.
randInt(min value, max value,
number of data in set)
randInt(1, 6, 6)
What are the results of these trials?
We received all 6 numbers only 1 out of 20 times.
What predictions can be made based on these
results?
There’s approximately a 5% chance of this occurring.
The more trials you run, the closer you will get to the
theoretical probability (Law of Large Numbers).
On a certain day the blood bank needs 4 donors with
type O blood. If the hospital brings in groups of five,
what is the probability that a group would arrive
that satisfies the hospitals requirements, assuming
that 45% of the population has type O blood?
Let 1-45 represent people with type O blood.
Let 46-100 represent people with other blood types.
Remember to seed the calculator to 5!
Then, run RandInt(1, 100, 5) twenty times.
Record how many trials satisfy the hospital’s
requirements.
To seed your calculator:
MATH, PRB, 5, STO →, RAND, ENTER
To run the simulation:
MATH, PRB, RandInt(1, 100, 5), ENTER
Five of the twenty groups have four or more
members with type O blood. Therefore, there is
a 25% chance that they hospital will get the
Type O blood they need.
Questions
about
simulations?
Expected Value and Fair Games
Expected Value
Expected value is the weighted average of all
possible outcomes.
For example, a trial has the outcomes 10, 20
and 60.
The average of 10, 20, and 60 = 30
This assumes an even distribution:



Sometimes,
outcomes will not
have equal
likelihoods.
X
1
2
3
P(X)
.5
.25
.25
E(X) = .5(1) + .25(2) + .25(3) = 1.75
You play a game in which you roll one fair die. If you
roll a 6, you win $5. If you roll a 1 or a 2, you win $2.
If you roll anything else, you lose.
Create a probability model for this game:
6
1, 2 3, 4, 5
$5
$2
$0
X
P(X) 1/6
1/3
1/2
What would you be willing to pay to play?
E(X) = 5(1/6) + 2(1/3) + 0(1/2) = 1.50
A price of $1.50 makes this a fair game.
At Tucson Raceway Park, your horse, My Little Pony,
has a probability of 1/20 of coming in first place, a
probability of 1/10 of coming in second place, and a
probability of ¼ of coming in third place. First place
pays $4,500 to the winner, second place $3,500 and
third place $1,500. Is it worthwhile to enter the race if
it costs $1,000?
1st
X
P(X)
2nd
$3500 $2500
.05
.10
3rd
Other
$500
-$1000
.25
.60
E(X) = .05(3500) + .1(2500) + .25(500)+.6(-1000) =
-$50.
What does an expected value of -$50 mean?
Its important to note that nobody will actually
lose $50—this is not one of the options. Over a
large number of trials, this will be the average loss
experienced.
This is the Law of Large Numbers!
Insurance companies and casinos build their
businesses based on the law of large numbers.
Questions about expected value?
Any
questions
about
statistics?