Download File

Graphs, Linear Equations, and
Functions
•
•
•
•
•
•
•
•
3-1
3-2
3-3
3-5
3.6
3.7
3.8
3.9
The Rectangular Coordinate System
Graphs of Equations
Lines
Introduction to Functions
Quadratic Functions
Operations on Functions
Inverse Functions
Variation
1
The
Rectangular Coordinate
System
Section 3.1
2
Objectives:
• Identify parts of the rectangular coordinate
system.
• Graph linear equations using an x-y chart and
using x and y intercepts.
• Graph horizontal and vertical lines.
• Use a graphing calculator to analyze data
involving linear equations.
• Apply the distance and midpoint formulas.
3
3-1 The Rectangular Coordinate System
Plotting ordered pairs.
An “ordered pair” of numbers is a pair of
numbers written within parenthesis in which
the order of the numbers is important.
• Example 1: (3,1), (-5,6), (0,0) are ordered pairs.
Note: The parenthesis used to represent an ordered pair are also
used to represent an open interval. The context of the problem tells
whether the symbols are ordered pairs or an open interval.
Graphing an ordered pair requires the use of graph paper and the
use of two perpendicular number lines that intersect at their 0 points.
The common 0 point is called the “origin”. The horizontal number
line is referred to as the “x-axis” or “abscissa” and the vertical line is
referred to as the “y-axis” or “ordinate”. In an ordered pair, the first
number refers to the position of the point on the x-axis, and the
second number refers to the position of the point on the y-axis.
4
3-1 The Rectangular Coordinate System
Plotting ordered pairs.
The x-axis and the y-axis
make up a “rectangular or
Cartesian” coordinate
system.
• Points are graphed by moving the
appropriate number of units in the x
direction, than moving the appropriate
number of units in the y direction.
(point A has coordinates (3,1), the point
was found by moving 3 units in the
positive x direction, then 1 in the
positive y direction)
• The four regions of the graph are called
quadrants. A point on the x-axis or yaxis does not belong to any quadrant
(point E). The quadrants are numbered.
5
3-1 The Rectangular Coordinate System
Finding ordered pairs that satisfy a given
equation.
To find ordered pairs that satisfy an equation, select any
number for one of the variables, substitute into the equation that
value, and solve for the other variable.
• Example 2: For 3x – 4y = 12, complete the table shown:
Solution
Given:
Equation
Solution
X
0
Y
0
-12
-4
x=0
3x - 4y =12
3(0) -4y = 12
y = -3
y=0
3x - 4(0) =12
x=4
y = -12
3x - 4(-12) = 12
x = -12
x = -4
3(-4) -4y = 12
y = -6
X
0
4
Y
-3
0
-12
-12
-4
-6
6
Intercepts of a Line
• The point where the line intersects the x-axis is (x,
0) and is called the x-intercept. To find the value of
x, substitute 0 in for y and solve for x.
• The point where the line intersects the y-axis is (0,
y) and is called the y-intercept. To find the value of
y, substitute 0 in for x and solve for y.
7
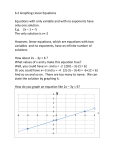
Graph the linear equation using x
and y intercepts
• Graph -2x + 4y = 8
8
Graph using either method
• 2(x -1) = 6 - 8y
9
Equations of Horizontal and Vertical
lines
• If a and b are real numbers then:
– The graph of x = a is a vertical line with x-intercept
(a, 0).
x = 3, x = -2, x = 7/9, x = -7.5
– The graph of y = b is a horizontal line with yintercept (0, b).
y = 5, y = -1, y = 2/3, y = -3.4
10
Graph x = 2
Graph y = -3
11
The Distance Formula
d  ( x2  x1 )  ( y2  y1 )
2
2
• Used to find the distance between any two points
in a rectangular coordinate system.
• The distance formula can be derived by plotting
two points (x1, y1) and (x2, y2), then form a right
triangle, and apply the Pythagorean theorem.
12
Find the distance between
P(-2, -5) and Q(3, 7)
13
The Midpoint Formula
 x1  x2 y1  y2 
,


2 
 2
•The point M that is half way or midway
between points P(x1, x2) and Q(y1,, y2) is
called the midpoint.
•The midpoint is average of the x-coordinates
and the average of the y-coordinates
14
Find the midpoint of the segment joining the
points P(-7, -8) and Q(1, -4)
15
If the midpoint of the segment is M(2, -5) and
one endpoint is P (6, 9), find the coordinates
of the other endpoint Q.
16
Important Information
• The graph of a linear equation is a straight line.
• Know how to graph a linear equation using an x-y
chart and using x and y intercepts.
• Know that x = constant is a vertical line.
• Know that y = constant is a horizontal line.
• Know the distance formula and the midpoint
formula.
17
3-1 The Rectangular Coordinate System
Graphing lines:
• Example 3: Draw the graph of 2x + 3y = 6
Step 1: Find a table of ordered pairs that satisfy the equation.
Step 2: Plot the points on a rectangular coordinate system.
Step 3: Draw the straight line that would pass through the
points.
Step 1
Step 2
Step 3
18
3-1 The Rectangular Coordinate System
Finding Intercepts:
In the equation of a line, let y = 0 to find the “x-intercept” and
let x = 0 to find the “y-intercept”.
Note: A linear equation with both x and y variables will have
both x- and y-intercepts.
• Example 4: Find the intercepts and draw the graph of 2x –y = 4
x-intercept: Let y = 0 : 2x –0 = 4
2x = 4
x=2
y-intercept: Let x = 0 : 2(0) – y = 4 -y = 4
y = -4
x-intercept is (2,0)
y-intercept is (0,-4)
19
3-1 The Rectangular Coordinate System
Recognizing equations of vertical and
horizontal lines:
An equation with only the variable x will always intersect the xaxis and thus will be vertical.
An equation with only the variable y will always intersect the yaxis and thus will be horizontal.
• Example 6: A) Draw the graph of y = 3
B) Draw the graph of x + 2 = 0
x = -2
A)
B)
20
3-1 The Rectangular Coordinate System
Graphing a line that passes through the
origin:
Some lines have both the x- and y-intercepts at the origin.
Note: An equation of the form Ax + By = 0 will always pass
through the origin. Find a multiple of the coefficients of x and y
and use that value to find a second ordered pair that satisfies the
equation.
• Example 7:
A) Graph x + 2y = 0
21
3.1 Homework Answers
15. d ( A, C )  d ( A, B)  d ( B, C )
2
2
25. d ( P, O)  5
2
( x  0) 2  ( y  0) 2  5
 
2
( 130 )  ( 98 )  32
1
Area  ( 32 )( 98 )  28
2
2
2
17. d ( A, B)  d ( B, C )  d (C, D)  d ( D, A) 
Radius = 5, Center = (0,0)
29
d ( A, C ) 2  d ( A, B) 2  d ( B, C ) 2
d ( A, C )  58
19.  3  x  5
2
8 y
 10
2
27.
d ( P, O )  6  (0  5) 2  ( y  3) 2
36  25  y 2  6 y  9
y  3  11
(0,3  11)
29. 5 
5x  2 y  3
and
(0,3  11)
(2a  1) 2  (a  3) 2
25  4a 2  4a  1  a 2  6a  9
0  (a  3)( a  1)
21. d ( A, C )  d ( B, C )  145
23. d ( A, P)  d ( B, P)
( x  4) 2  ( y  3) 2  ( x  6) 2  ( y  1) 2
Pick a pt. Q(0,y) on y-axis
38.
Since y-coord. is – in the third
quad. a = -1. (-2,-1)
 1920  1940 2042  1878 
,


2
2


1930,1960
3.2 Solving Polynomial Equations
by Graphing
23
3-2 The Slope of a Line
Finding the slope of a line given two
points on the line:
The slope of the line through two distinct points
(x1, y1) and (x2, y2) is:
rise change in y y2  y1
slope  m 


run change in x x2  x1
( x 2  x1 )
Note: Be careful to subtract the y-values and the x-values in the
same order.
Correct
Incorrect
y2  y1
y1  y2
or
x2  x1
x1  x2
y2  y1
y1  y2
or
x1  x2
x2  x1
24
Types of Equations
• Quadratic - has the form ax2 + bx +
c=0
• Highest exponent is two (this is the
degree)
• The most real solutions it has is two.
25
Types of Equations
• Cubic - has the form
ax3 + bx2
+ cx + d = 0
• Highest exponent is three (this is the
degree)
• The most real solutions it has is three.
26
Types of Equations
• Quartic - has the form ax4 + bx3 + cx2
+ dx + e = 0
• Highest exponent is four (this is the
degree)
• The most real solutions it has is four.
27
Types of Equations
• These keep on going up as the
highest exponent increases.
• You don’t need to know the names
above quartic, but you do need to be
able to give the degree.
28
29
The standard form of the equation of a circle with
its center at the origin is
x y r
2
2
2
r is the radius of the circle so if we take the square root of the
right hand side, we'll know how big the radius is.
Notice that both the x and y terms are squared. Linear
equations don’t have either the x or y terms squared.
Parabolas have only the x term was squared (or only the
y term, but NOT both).
30
Let's look at the equation
x  y 9
2
2
This is r2 so r = 3
The center of the circle is at the origin and the radius is 3.
Let's graph this circle.
Count out 3 in all
directions since
that is the radius
Center at (0, 0)
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
31
If the center of the circle is NOT at the origin then the
equation for the standard form of a circle looks like this:
x  h    y  k 
2
2
r
The center of the circle is at (h, k).
x  3   y  1
2
2
2
This is r2 so r = 4
 16
Find the center and radius and graph this circle.
The center of the circle is at (h, k) which is (3,1).
The radius is 4
- - - - - - -
12345678
7 6 5 4 3 2 10
32
If you take the equation of a circle in standard form for
example:
2
2
This is r2 so r = 2
x2  y4  4

 

(x - (-2))
Remember center is at (h, k) with (x - h) and (y - k)
since the x is plus something and not minus, (x + 2)
can be written as (x - (-2))
You can find the center and radius easily.
The center is at (-2, 4) and the radius is 2.
But what if it was not in standard form but multiplied out (FOILED)
x  4 x  4  y  8 y  16  4
2
2
Moving everything to one side in descending order and
combining like terms we'd have:
x  y  4 x  8 y  16  0
2
2
33
x  y  4 x  8 y  16  0
2
2
If we'd have started with it like this, we'd have to complete the
square on both the x's and y's to get in standard form.
Group x terms and a place Group y terms and a place
to complete the square
to complete the square
Move constant
to the other side
2
4
16  16  ___
4  ___
16
x  4 x  ____  y  8 y  ____
2
Complete the square
Write factored and wahlah! back in standard form.
x  2   y  4
2
2
4
34
Now let's work some examples:
Find an equation of the circle with center at (0, 0) and radius 7.
Let's sub in center and radius values in the standard form
x  0h   y  k0 
2
2
 7r
2
x  y  49
2
2
35
Find an equation of the circle with center at (0, 0) that passes
through the point (-1, -4).
Since the center is at (0, 0) we'll have
x y r
2
2
2
The point (-1, -4) is on the circle so should work when
we plug it in the equation:
 1   4
2
2
r
2
 1 16  17
Subbing this in for r2 we have:
x  y  17
2
2
36
Find an equation of the circle with center at (-2, 5) and radius 6
Subbing in the values in standard form we have:
x -2h   y  k5 
2
2
 x  2    y  5
2
2
 6r
2
 36
37
Find an equation of the circle with center at (8, 2) and passes
through the point (8, 0).
Subbing in the center values in standard form we have:
x  8h   y  k2 
2
2
r
2
Since it passes through the point (8, 0) we can plug this
point in for x and y to find r2.
8  8  0  2
2
2
r
2
 x  8   y  2 
2
2
4
4
38
Identify the center and radius and sketch the graph:
9 x  9 y  64
2
2
9
9
9
To get in standard form we don't want coefficients on the
squared terms so let's divide everything by 9.
64
x y 
9
2
2
Remember to square
root this to get the
radius.
So the center is at (0, 0) and the radius is 8/3.
- - - - - - -
12345678
7 6 5 4 3 2 10
39
Identify the center and radius and sketch the graph:
x  4   y  3
2
2
 25
Remember the center values end up being the opposite sign of what
is with the x and y and the right hand side is the radius squared.
So the center is at (-4, 3) and the radius is 5.
- - - - - - - 01 234 56 78
765432 1
40
Find the center and radius of the circle:
x  y  6x  4 y  3  0
2
2
We have to complete the square on both the x's and y's to get in
standard form.
Group x terms and a place Group y terms and a place
to complete the square
to complete the square
Move constant
to the other side
2
9
4  3  ___
9  ___
4
x  6 x  ____  y  4 y  ____
2
Write factored for standard form.
x  3   y  2
2
2
 16
So the center is at (-3, 2) and the radius is 4.
41
3.2 day 2 Homework Answers
x  9  y2
x2  y2  9
33.
41. r = 3
43. (-4,4)
45. Midpt =
(1,2) = center
r
1
(diam.)
2
1
( 136 )
2
 34

( x  1) 2  ( y  2) 2  34
61. If distance from P to C
is less than r, greater
than r, or = to r
63. x – int. (0 for y)
x2  4x  4  0
x2
y – int. (0 for x)
y2  6 y  4  0
y 2  6 y  9  4  9
y  3 5
65.x 2  4 x  4  y 2  6 y  9  9
( x  2) 2  ( y  3) 2  9
c(2,3) r  3
dP(2,6)  d ( P, C )  16  9  25  5
( x  2) 2  ( y  3) 2  25
3-3 Lines
The slope of a line
Finding the slope of a line given two points on
the line:
• Example 1) Find the slope of the line through the points
(2,-1) and (-5,3)
rise y2  y1 3  (1)
4
4
slope  m 

=


run x2  x1 (5)  2 7
7
43
3-3 The Slope of a Line
Finding the slope of a line given an equation of
the line: The slope can be found by solving the
equation such that y is solved for on the left
side of the equal sign. This is called the slopeintercept form of a line. The slope is the
coefficient of x and the other term is the yintercept. The slope-intercept form is
y = mx + b
• Example 2) Find the slope of the line given 3x – 4y = 12
3 x  4 y  12
4 y  3 x  12
3
y  x3
4
3
 The slope is
4
44
3-3 The Slope of a Line
Finding the slope of a line given an equation of
the line:
• Example 3) Find the slope of the line given y + 3 = 0
y = 0x - 3
The slope is 0
• Example 4) Find the slope of the line given x + 6 = 0
Since it is not possible to solve for y, the slope is “Undefined”
Note: Being undefined should not be described as “no slope”
• Example 5) Find the slope of the line given 3x + 4y = 9
3x  4 y  9
3
4 y  3x  9  The slope is - 4
3
9
y  x
4
4
45
3-3 The Slope of a Line
Graph a line given its slope and a point on the
line: Locate the first point, then use the slope
to find a second point.
Note: Graphing a line requires a minimum of two points. From the
first point, move a positive or negative change in y as indicated by the
value of the slope, then move a positive value of x.
• Example 6) Graph the line given
2
slope =
passing through (-1,4)
3
Note: change in y is +2
46
3-3 The Slope of a Line
Graph a line given its slope and a point
on the line: Locate the first point, then use the
slope to find a second point.
• Example 7) Graph the line given
slope = -4 passing through (3,1)
Note:
A positive slope indicates the line moves up from L to R
A negative slope indicates the line moves down from L to R
47
3-3 The Slope of a Line
Using slope to determine whether two lines are
parallel, perpendicular, or neither:
Two non-vertical lines having the same slope are parallel.
Two non-vertical lines whose slopes are negative reciprocals
are perpendicular.
• Example 8) Is the line through (-1,2) and (3,5) parallel to the line
through (4,7) and (8,10)?
For line 1:
52
3
m1 

3  (1) 4
 YES
For line 2:
10  7 3
m2 

84 4
48
3-3 The Slope of a Line
Using slope to determine whether two lines are
parallel, perpendicular, or neither:
Two non-vertical lines having the same slope are parallel.
Two non-vertical lines whose slopes are negative reciprocals are perpendicular.
• Example 9) Are the lines 3x + 5y = 6 and 5x - 3y = 2 parallel,
perpendicular, or neither?
For line 1:
3x  5 y  6
5 y  3x  6
For line 2:
5x - 3 y  2
 3 y  5 x  2
3
6
5
2
y  x
y  x
5
5
3
3
3
5
 is the negative reciprocal of
5
3
 Perpendicular
49
3-3 The Slope of a Line
Solving Problems involving average rate
of change: The slope gives the average rate of change in y
per unit change in x, where the value of y depends on x.
• Example 10) The graph shown approximates the percent of
US households owing multiple pc’s in the years 1997-2001.
Find the average rate of change between years 2000 and 1997.
Use the ordered pairs:
(1997,10) and (2000,20.8)
20.8  10
10.8
%
m

 3.6
2000  1997
3
yr
50
3-3 The Slope of a Line
Solving Problems involving average rate
of change: The slope gives the average rate of change in y
per unit change in x, where the value of y depends on x.
• Example 11) In 1997, 36.4 % of high school students smoked.
In 2001, 28.5 % smoked.
Find the average rate of change in percent per year.
Use the ordered pairs:
(1997,36.4) and (2001,28.5)
28.5  36.4 7.9
%
m

 1.975
2001  1997
4
yr
51
3-3 Linear Equations in Two Variables
Writing an equation of a line given its slope
and y-intercept: The slope can be found by
solving the equation such that y is solved for
on the left side of the equal sign. This is called
the slope-intercept form of a line. The slope is
the coefficient of x and the other term is the yintercept.
The slope-intercept form is y = mx + b, where
m is the slope and b is the y-intercept.
• Example 1: Find an equation of the line with slope 2 and yintercept (0,-3)
Since m = 2 and b = -3,
y = 2x - 3
52
3-3 Linear Equations in Two Variables
Graphing a line using its slope and yintercept:
• Example 2: Graph the line using the slope and yintercept: y = 3x - 6
Since b = -6, one point on the line is (0,-6).
Locate the point and use the slope (m = 3 ) to locate a
1
second point.
(0+1,-6+3)=
(1,-3)
53
3-3 Linear Equations in Two Variables
Finding equations of Parallel or
Perpendicular lines:
If parallel lines are required, the slopes are identical.
If perpendicular lines are required, use slopes that are
negative reciprocals of each other.
• Example 5: Find an equation of a line passing through the
point (-8,3) and parallel to 2x - 3y = 10.
Step 1: Find the slope
of the given line
2x – 3y = 10
-3y = -2x + 10
-3
-3
y = 2/3x – 10/3
m = 2/3
Step 2: Use slope-intercept form
y = mx + b
y = 2/3 x + b
3 = 2/3 (-8) + b
3 = -16/3 + b
25/3 = b
y = 2/3x + 25/3
54
3-3 Linear Equations in Two Variables
Finding equations of Parallel or
Perpendicular lines:
• Example 6: Find an equation of a line passing through the
point (-8,3) and perpendicular to 2x - 3y = 10.
Step 1: Find the slope
of the given line
2 x  3 y  10
3 y  2 x  10
y
2
10
x
3
3
 m
2
3
Step 2: Take the negative reciprocal
Step 3: Use slope-intercept form
y = mx + b
y = -3/2x + b
3 = (-3/2)(-8) + b
3 = 12 + b
-9 = b
y = -3/2x - 9
of the slope found
2
3
m
 m1  
3
2
55
3-3 Linear Equations in Two Variables
Forms of Linear Equations
Equation
Description
When to Use
Y = mx + b
Slope-Intercept Form
slope is m
y-intercept is (0,b)
Given an equation, the slope
and y-intercept can be easily
identified and used to graph
y - y1 = m(x-x 1)
Point-Slope Form
slope is m
line passes through (x 1,y1)
This form is ideal to use when
given the slope of a line and
one point on the line or given
two points on the line.
Standard Form
(A,B, and C are integers, A  0)
Slope is -(A/B)
x-intercept is (C/A,0)
y-intercept is (0,C/B)
Horizontal line
slope is 0
y-intercept is (0,b)
X- and y-intercepts can be found
quickly
Ax + By = C
y=b
x=a
Vertical line
slope is undefined
x-intercept is (a,0)
Graph intersects only the y
axis, is parallel to the x-axis
Graph intersects only the x
axis, is parallel to the y-axis
56
3-3 Linear Equations in Two Variables
Writing an equation of a line that
models real data: If the data changes at a fairly
constant rate, the rate of change is the slope. An initial
condition would be the y-intercept.
• Example 7: Suppose there is a flat rate of $.20 plus a
charge of $.10/minute to make a phone call. Write an
equation that gives the cost y for a call of x minutes.
Note: The initial condition is the flat rate of $.20 and the
rate of change is $.10/minute.
Solution:
y = .10x + .20
57
3-3 Line of best fit
Writing an equation of a line that
models real data: If the data changes at a fairly
constant rate, the rate of change is the slope. An initial
condition would be the y-intercept.
• Example 8: The percentage of mothers of children
under 1 year old who participated in the US labor force
is shown in the table. Find an equation that models the
data.
Year
Percent
Using (1980,38) and (1998,50)
1980
38
59  38
21
m

1998  1980 18
m  1.167
1984
1988
1992
1998
47
51
54
59
 y  1.167 x  38
58
3.3 Homework Answers
11. A(-1,3) is 5 units to the left and 5 units downs from B(4,2). D will have
the same relative position (-7-5,5-5) = (-12,0).
35.
1 5 5 5  1

midpt ( A, B)   , 
   b  y  5 x  30

2 2 2 7  2
7
14
5 x  7 y  15
30
7
14 y  10 x  30
b
slope ( A, B) 
14
5
37. m=-1 thru origin and y = -x
47. (x-3)2+(y+2)2 = 49
53. a)
50
5
x x
14
b) 14  0
x  162
y
55.a)
20
m
3
b)
56. a)
5
(162)  58
14
20
w
t  10
3
20
w  t  10  50
c)
3
w  70
t 9
70 
20
t  10
3
8125  m(1)  8250
p  125t  8250
b) P  5000
t  26
c) 8250
 66
125
m  125
 125t  8250  5000
3-4 Introduction to Functions
Defining and Identifying Relations
and Functions: If the value of the variable y
depends upon the value of the variable x, then y is the
dependent variable and x is the independent variable.
• Example 1: The amount of a paycheck depends upon
the number of hours worked. Then an ordered pair
(5,40) would indicate that if you worked 5 hours, you
would be paid $40. Then (x,y) would show x as the
independent variable and y as the dependent variable.
A relation is a “set of ordered pairs”.
{(5,40), (10,80), (20,160), (40,320)} is a relation.
60
3-4 Introduction to Functions
Defining and Identifying Relations and Functions:
A function is a relation such that for each value of the
independent variable, there is one and only one value of the
dependent variable.
Note: In a function, no two ordered pairs can have the same
1st component and different 2nd components.
• Example 2: Determine whether the relation is a function
{(-4,1), (-2,1), (-2,0)}
Solution: Not a function, since the independent variable
has more than one dependent value.
61
3-4 Introduction to Functions
Defining and Identifying Relations and Functions:
Since relations and functions are sets of ordered pairs, they
can be represented as tables or graphs. It is common to
describe the relation or function using a rule that explains the
relationship between the independent and dependent variable.
Note: The rule may be given in words or given as an equation.
y = 2x + 4
where x is the independent variable
and y is the dependent variable
x
0
2
4
6
y
4
8
12
16
62
3-4 Introduction to Functions
Domain and Range:
In a relation:
A) the set of all values of the independent variable (x) is the domain.
B) the set of all values of the dependent variable (y) is the range.
• Example 3: Give the domain and range of each relation. Is the
relation a function?
{(3,-1), (4,-2),(4,5), (6,8)}
Domain: {3,4,6}
Range: {-1,-2,5,8}
Not a function
• Example 4: Give the domain and range of each relation. Is the
relation a function?
x
y
Domain: {0,2,4,6}
0
4
Range: {4,8,12,16}
2
4
6
8
12
16
63
3-4 Introduction to Functions
Domain and Range:
In a relation:
A) the set of all values of the independent variable (x) is the domain.
B) the set of all values of the dependent variable (y) is the range.
• Example 4: Give the domain and range of each relation. Is the
relation a function?
Domain:
{1994,1995,1996,1997,1998,1999}
Range:
{24134,33786,44043,55312,69209,86047}
This is a function
Cell Phone Users
Subscribers
Year
(thousands)
1994
24,134
1995
33,786
1996
44,043
1997
55,312
1998
69,209
1999
86,047
64
3-4 Introduction to Functions
Domain and Range:
In a relation:
A) the set of all values of the independent variable (x) is the
domain.
B) the set of all values of the dependent variable (y) is the range.
• Example 5: Give the domain and range of each relation.
Domain: (-,  )
Domain: [-4, 4]
Range: (-, 4]
Range: [-6, 6]
65
3-4 Introduction to Functions
Agreement on Domain:
Unless specified otherwise, the domain of a relation is assumed
to be all real numbers that produce real numbers when
substituted for the independent variable.
1
y
• The function
x has all real numbers except x = 0 Note: In
general, the domain of a function defined by an algebraic
expression is all real numbers except those numbers that lead
to division by zero or an even root of a negative number.
• The function y  3 x  2 is not defined for values < 2
3
66
3-4 Introduction to Functions
Identifying functions defined by graphs
and equations:
Vertical Line Test:
If every vertical line intersects the graph of a relation
in no more than one point, the relation represents a
function .
67
3-4 Introduction to Functions
Identifying functions defined by graphs and
equations:
Vertical Line Test:
If every vertical line intersects the graph of a relation in no
more than one point, the relation represents a function.
Function
Not a Function
68
3-4 Introduction to Functions
Identifying functions defined by graphs and
equations:
• Example 5: Decide whether the equations shown define a function and give
the domain
y  3x  2
y
5
x 1
y2  x
Function
Function
Not a Function
Domain:
Domain:
Domain:
2 
 3 ,  
 ,1 1, 
0,
69
3-4 Introduction to Functions
Using Function Notation:
When a rule or equation is defined such that y is dependent on
x, the “Function Notation” y = f(x) is used and is read as “y = f
of x” where the letter f stands for function.
Note: The symbol f(x) does not indicate that f is multiplied by
x, but represents the y-value for the indicated x-value.
If y = 9x -5, then f(x) = 9x -5 and f(2) = 9(2) -5 = 13
and f(0) = 9(0) -5 = -5
• Example 6:
3x  5
2
Find : f (3) and f (r )
3(3)  5 9  5 14
f (3) 


7
2
2
2
3r  5
f (r ) 
2
f ( x) 
70
3-4 Introduction to Functions
Using Function Notation:
When a rule or equation is defined such that y is dependent on
x, the “Function Notation” y = f(x) is used and is read as “y = f
of x” where the letter f stands for function.
• Example 7: f(x) = 5x -1 find: f(m + 2)
f(m + 2) = 5(m + 2) -1 = 5m + 10 - 1
f(m + 2) = 5m + 9
• Example 8: Rewrite the equation given and find f(1) and f(a)
x2  4 y  3
Find : f (1) and f (a)
4 y   x  3
2
x2  3
y
4
x2  3
f ( x) 
4
Find : f (1) and f (a )
(1) 2  3 2
1
f (1) 


4
4
2
a2  3
f (a) 
4
71
3-4 Introduction to Functions
Identifying Linear Functions:
A function that can be defined by f(x) = mx + b for real
numbers m and b is a “Linear Function”
The domain of a linear function is (-, ).
The range is (-, ).
Note: Remember that m represents the slope of a line and (0,b)
is the y-intercept.
Note:
A function that can be defined by f(x) = b is called a “Constant
Function” which has a graph that is a horizontal line.
Note:
The range of a constant function is {b}.
72
3.4 Homework Answers
7. a) f (a)  a 2  4
2
2
15. a) [-3,4]
b) f (a)  (a)  4  a  4
2
2
b) [-2,2]

f
(
a
)


(

a

4
)

a
4
c)
2
2
c) f(1)=0
f
(
a

h
)


a

2
ah

h

4
d)
d) x= -1, .5, 2
2
2
9. a) x  x  3  a  a  3
e) (-1, .5) or (2,4]
2
2
b)  1(a  a  3)  a  a  3
31. D  (, )
c)  a 2  (a)  3  a 2  a  3
R  (, )
2
d) a  h  a  h  3
Increas.(, )
e) (a 2  a  3)  (h 2  h  3)
33. D  (, ),
f) (a  2ah  h  a  h  3)  (a  a  3)
R  (,4)

 
2
2
2
h
4
11. a) 2
a 1
b)
4a 2
c) 4a
d)
2a

Increas.(,0]
Decreas.[0, )
D  [4, )
R  [0, )
35.
Increas.[4, )
37.
D  (, )
R  {2}
Const.(, )
D  [6,6]
39. Dec.[6,0]
R  [6,0]
Inc.[0,6]
73
Symmetric about the y axis
FUNCTIONS
Symmetric about the origin
3.5 Graphs of Functions
74
Even functions have y-axis Symmetry
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-2
-3
-4
-5
-6
-7
So for an even function, for every point (x, y) on
the graph, the point (-x, y) is also on the graph.
3.5
75
Odd functions have origin Symmetry
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-2
-3
-4
-5
-6
-7
So for an odd function, for every point (x, y) on the
graph, the point (-x, -y) is also on the graph.
3.5
76
x-axis Symmetry
We wouldn’t talk about a function with x-axis symmetry
because it wouldn’t BE a function.
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-2
-3
-4
-5
-6
-7
3.5
77
A function is even if f( -x) = f(x) for every number x in
the domain.
So if you plug a –x into the function and you get the
original function back again it is even.
f x   5 x  2 x  1
4
2
Is this function even?
YES
f  x   5( x)  2( x)  1  5x  2 x  1
4
2
4
2
f x   2 x  x Is this function even?
NO
3
3
f  x   2( x)  ( x)  2 x  x 3.5
3
78
A function is odd if f( -x) = - f(x) for every number x in
the domain.
So if you plug a –x into the function and you get the
negative of the function back again (all terms change signs)
it is odd.
f x   5 x  2 x  1
4
2
Is this function odd?
NO
f  x   5( x)  2( x)  1  5x  2 x  1
4
2
4
2
f x   2 x  x Is this function odd? YES
3
3
f  x   2( x)  ( x)  2 x  x
3
79
If a function is not even or odd we just say neither
(meaning neither even nor odd)
Determine if the following functions are even, odd or
neither.
Not the original and all
3
terms didn’t change
signs, so NEITHER.
f x   5 x  1
f  x   5 x   1  5 x  1
3
3
f x   3x  x  2
4
2
Got f(x) back so
EVEN.
f  x   3( x)  ( x)  2  3x  x  2
4
2
4
2
80
GREATEST INTEGER FUNCTION
When greatest integer acts on a number, the value that
represents the result is the greatest integer that is less
than or equal to the given number. There are several
descriptors in that expression. First of all you are looking
only for an integer. Secondly, that integer must be less
than or equal to the given number and finally, of all of the
integers that satisfy the first two criteria, you want the
greatest one. The brackets which indicate that this
operation is to be performed is as shown: ‘[ ]’.
Example: [1.97] = 1
Example: [-1.97] = -2
There are many integers less than 1.97; {1,
0, -1, -2, -3, -4, …} Of all of them, ‘1’ is the
greatest.
There are many integers less than -1.97;
{-2, -3, -4, -5, -6, …} Of all of them, ‘-2’ is
the greatest.
81
It may be helpful to visualize this function a little more clearly by
2
using a number line.  14
-6.31
-7
-6
5
-5
-4
-3
6.31
3
-2
Example: [6.31] = 6
-1
0
1
2
3
4
5
6
7
8
Example: [-6.31] = -7
When you use this function, the answer is the integer on the immediate
left on the number line. There is one exception. When the function
acts on a number that is itself an integer. The answer is itself.
Example: [5] = 5
 
2 
Example:    0 .6  0
3
Example: [-5] = -5
  14 
  2 .8    3
Example: 

 5 
If there is an operation inside the greatest integer brackets, it must
be performed before applying the function.
Example: [5.5–3.6] = [1.9] = 1
Example: [3.6–5.5] = [-1.9] = -2
Example: [5.5+3.6] = [9.1] = 9
Example: [5.53.6] = [19.8] = 19
82
2.01
1.99
1
2
3
Example: [5–2.99] = [2.01] = 2
Example: [5–3] = [2] = 2
Example: [5–3.01] = [1.99] = 1
The greatest integer function can be used to construct a Cartesian
graph. The simplest of which is demonstrated below.
f(x) = [x]
To see what the graph looks like, it is necessary to determine some
ordered pairs which can be determined with a table of values.
x
0
1
2
3
-1
-2
f(x) = [x]
f(0) = [0] = 0
f(1) = [1] = 1
f(2) = [2] = 2
f(3) = [3] = 3
f(-1) = [-1] = -1
If we only choose integer
values for x then we will not
really see the function
manifest itself. To do this
we need to choose noninteger values.
f(-2) = [-2] = -2
83
x
f(x) = [x]
0 f(0) = [0] = 0
0.5 f(0.5) = [0.5] = 0
0.7 f(0.7) = [0.7] = 0
0.8 f(0.8) = [0.8] = 0
0.9 f(0.9) = [0.9] = 0
1
f(1) = [1] = 1
1.5 f(1.5) = [1.5] = 1
1.6 f(1.6) = [1.6] = 1
1.7 f(1.7) = [1.7] = 1
1.8 f(1.8) = [1.8] = 1
1.9 f(1.9) = [1.9] = 1
2
f(2) = [2] = 2
-0.5 f(-0.5) =[-0.5]=-1
-0.9 f(-0.9) =[-0.9]=-1
-1
f(-1) = [-1] = -1
84
When all these
points are strung
together the graph
looks something like
this – a series of
steps.
For this reason it is
sometimes called the
‘STEP FUNCTION’.
Notice that the left
of each step begins
with a closed
(inclusive) point but
the right of each step
ends with an open
(excluding point)
We can’t really
state the last (most
right) x-value on
each step because
there is always
another to the right
of the last one you
may name. So
instead we describe
the first x-value
that is NOT on a
given step.
Example: (1,0)
85
Rather than place a
long series of points
on the graph, a line
segment can be
drawn for each step
as shown to the
right.
The graphs shown
thus far have been
magnified to make a
point. However,
these graphs are
usually shown at a
normal scale as you
can see on the next
slide.
86
f(x) = [x]
In these 3
examples,
parameter ‘a’ is
changed. As a
increases, the
distance between
the steps
increases.
a=1
f(x) = 2[x]
a=2
a=3
f(x) = 3[x]
87
f(x) = -[x]
a = -1
f(x) = -2[x]
a = -2
When ‘a’ is negative, notice that the slope of the steps is changed.
Downstairs instead of upstairs. But as ‘a’ changes from –1 to –2,
the distance between steps increases. The further that ‘a’ is
from 0, the greater the separation between steps. This can be
described with a formula.
Vertical distance between Steps = |a|
88
f(x) = [x]
b=1
f(x) = [2x]
b=2
1 
f (x )   x 
2 
b
1
2
As ‘b’ is increased
from 1 to 2, each step
gets shorter. Then
as it is decreased to
0.5, the steps get
longer.
1
Length of Step 
b
89
3.5 Homework Answers
1. f ( x)  5( x)  2( x)   f ( x) odd
3. f (x)  3(x)  2(x)  5  f ( x) even 39. a) shift 3 units left
5. f (x)  8(x)  3(x)   f ( x) neither b) shift 3 units right
c) shift up 3 units
7. f ( x)  ( x)  4  f ( x) even
d) shift down 3 units
9. f ( x)  ( x)  ( x)   f ( x) odd
3
4
2
3
2
2
3
3
11. Shift down 2, up 1, 41. a) f is shifted left 9 units and up 1
b) f is reflected through x-axis
up 3
c) f is reflected through x-axis and
13. Shift down 4, up 2,
shifted left 7 units and down 1
up 4
53. Not a function (9)
15. Shift down 3, up 2
57. Graph
17. Shift left 2, right 3
67. Graph
25. P(0,5); y=f(x-2)-1
71. Since g(x) = f(x)+4, the graph of g
(-2, 4)
can be obtained by shifting
31. Shifted 2 units to the
the graph of f up +4.
right and 3 units up
91
Quadratic Equation – Equation in the form y=ax2 + bx + c.
Parabola – The general shape of a quadratic equation. It is
in the form of a “U” which may open upward or downward.
Vertex – The maximum or minimum point of a parabola.
Maximum – The highest point (vertex) of a parabola
when it opens downward.
Minimum – The lowest point (vertex) of a parabola when
it opens upward.
Axis of symmetry – The line passing through the vertex
b about which the parabola is
having the equation
x
symmetric.
2a
92
How does the sign of the coefficient of x2 affect the graph of a
parabola?
On your graphing calculator, do the following:
1.
Press the Y= key.
2. Clear any existing equations by placing the cursor
immediately after the = and pressing CLEAR.
3. Enter 2x2 after the Y1= by doing the following
keystrokes.
4.
Press GRAPH.
93
Repeat using the equation y = -2x2.
When the coefficient of x2 is positive, the graph opens upward.
When the coefficient of x2 is negative, the graph opens downward.
94
How does the value of a in the equation ax2 + bx + c affect the
graph of the parabola?
Clear the equations in the Y= screen of your calculator.
Enter the equation x2 for Y1.
Enter the equation 3 x2 for Y2. Choose a different type of
line for Y2 so that you can tell the difference between them.
Press GRAPH.
95
Clear the second equation in the Y= screen and now enter
the equation y = (1/4)x2.
Press the GRAPH key and compare the two graphs.
96
Summary for ax2
When a is positive, the parabola opens upward.
 When a is negative, the parabola opens downward.
 When a is larger than 1, the graph will be narrower
than the graph of x2.
 When a is less than 1, the graph will be wider (broader)
than the graph of x2.
97
How does the value of c affect the graph of a parabola when
the equation is in the form ax2 + c?
o
In the Y= screen of the graphing calculator, enter x2 for Y1.
o
Enter x2 + 3 for Y2.
o
Press the GRAPH key.
98
Now predict what the graph of y = x2 – 5 will look like.

Enter x2 for Y1 in the Y= screen.

Enter x2 – 5 for Y2

Press GRAPH.
99
What happens to the graph of a parabola when the equation is
in the form (x-h)2 or (x+h)2?

Enter x2 for Y1 in the Y= screen.

Enter (x-3)2 for Y2.

Press GRAPH.
10

Clear the equation for Y2.

Enter (x+4)2 for Y2.

Press GRAPH.
10

The vertex of the graph of ax2 will be at the origin.
 The vertex of the graph of the parabola having the
equation ax2 + c will move up on the y-axis by the
amount c if c>0.
 The vertex of the graph of the parabola having the equation
ax2 + c will move down on the y-axis by the absolute value of c
if c<0.
 The vertex of the graph of the parabola in the form (x-h)2
will shift to the right by h units on the x-axis.
 The vertex of the graph of the parabola in the form
(x+h)2 will shift to the left by h units on the x-axis.
10
Compare the graphs of the following quadratic equations to
each other. Check your work with your graphing calculator.
1)
x2, x2 – 7, (x +2)2
2)
2x2,
x2 + 6, (1/3)(x-5)2
10
Problem 1

All three graphs have the same shape.
 The vertex of the graph of x2 – 7 will move down 7
on the y-axis.
 the vertex of the graph of (x+2)2 will move left two
on the x-axis.
10
Problem 2
 The graph of 2x2 will be the narrowest. The graph of
(1/3)(x-2)2 will be the broadest.
 The vertex of x2 + 6 will be shifted up 6 units on the yaxis compared to the graph of 2x2.
 The vertex of (1/3)(x-2)2 will be shifted right two units
on the x-axis compared to the graph of 2x2.
10
GRAPHS OF QUADRATIC FUNCTIONS
When the standard form of a quadratic
function f(x) = ax2 + bx + c is written in the
form:
a(x - h) 2 + k
We can tell by horizontal and vertical shifting
of the parabola where the vertex will be.
The parabola will be shifted h units
horizontally and k units vertically.
10
GRAPHS OF QUADRATIC FUNCTIONS
Thus, a quadratic function written in the form
a(x - h) 2 + k
will have a vertex at the point (h,k).
The value of “a” will determine whether the
parabola opens up or down (positive or
negative) and whether the parabola is narrow
or wide.
10
GRAPHS OF QUADRATIC FUNCTIONS
a(x - h) 2 + k
Vertex (highest or lowest point): (h,k)
If a > 0, then the parabola opens up
If a < 0, then the parabola opens down
10
GRAPHS OF QUADRATIC FUNCTIONS
Axis of Symmetry
The vertical line about which the graph
of a quadratic function is symmetric.
x=h
where h is the x-coordinate of the
vertex.
10
GRAPHS OF QUADRATIC FUNCTIONS
So, if we want to examine the
characteristics of the graph of a
quadratic function, our job is to
transform the standard form
f(x) = ax2 + bx + c
into the form
f(x) = a(x – h)2 + k
11
GRAPHS OF QUADRATIC FUNCTIONS
This will require to process of
completing the square.
11
GRAPHING QUADRATIC FUNCTIONS
Graph the functions below by hand by
determining whether its graph opens up
or down and by finding its vertex, axis of
symmetry, y-intercept, and x-intercepts,
if any. Verify your results using a
graphing calculator.
f(x) = 2x2 - 3
g(x) = x2 - 6x - 1
h(x) = 3x2 + 6x
k(x) = -2x2 + 6x + 2
11
EXAMPLE
Determine without graphing whether the
given quadratic function has a maximum
or minimum value and then find the
value. Verify by graphing.
f(x) = 4x2 - 8x + 3
g(x) = -2x2 + 8x + 3
11
FINDING A QUADRATIC FUNCTION
Determine the quadratic function whose
vertex is (1,- 5) and whose y-intercept is -3.
11
3.6 Homework Answers
3 2
y

34

( x  12 x  36)
11.
4
23. v(4,1)
y
y  a( x  4)  1
2
25. v(2,4) pt (1,0)
3
( x  6) 2  7
4
1
a
8
y  a( x  2) 2  4 a 
2
25

a
(
3

0
)
2
27.
4
9
a3
0  a(0  3) 2  5 a 
5
9
1
y  ( x  4) 2  1
8
y
4
( x  2) 2  4
9
y  3x 2  2
y
29.
pt (0,0)
31.
v(1,4), x  (3,0) 0  a(3  1) 2  4 a 
5
( x  3) 2  5
9
1
4
y   1 ( x  1) 2  4
4
4
9
45. y   ( x  )  3
27
2
60. a) up slightly, down slightly, although there is unexpected down in 1987
2
b)y  .07( x  1984)  7.6
11
The sum f + g
 f  g x  f x  gx
This just says that to find the sum of two functions, add
them together. You should simplify by finding like terms.
f x   2 x  3
g x   4 x  1
2
3
f  g  2x  3  4x 1
2
3
 4x  2x  4
3
2
Combine like
terms & put in
descending
order
11
The difference f - g
 f  g x  f x  gx
To find the difference between two functions, subtract
the first from the second. CAUTION: Make sure you
distribute the – to each term of the second function. You
should simplify by combining like terms.
f x   2 x  3
2

g x   4 x  1
3

f  g  2x  3  4x 1
2
3
Distribute
negative
 2 x  3  4 x  1  4 x  2 x  2
2
3
3
2
11
The product f • g
 f  g x  f x g x
To find the product of two functions, put parenthesis
around them and multiply each term from the first
function to each term of the second function.
f x   2 x  3
g x   4 x  1
2

3


f  g  2x  3 4x 1
2
3
 8 x  2 x  12 x  3
5
2
3
FOIL
Good idea to put in
descending order
but not required.
11
The quotient f /g
f
f x 
 x  
g x 
g
To find the quotient of two functions, put the first one
over the second.
f x   2 x  3
2
f 2x  3
 3
g 4x 1
2
g x   4 x  1
3
Nothing more you could do
here. (If you can reduce
these you should).
12
So the first 4 operations on functions are
pretty straight forward.
The rules for the domain of functions would
apply to these combinations of functions as
well. The domain of the sum, difference or
product would be the numbers x in the
domains of both f and g.
For the quotient, you would also need to
exclude any numbers x that would make the
resulting denominator 0.
12
COMPOSITION
FUNCTIONS
“SUBSTITUTING ONE FUNCTION INTO ANOTHER”
12
The Composition
Function
 f  g x  f gx
This is read “f composition g” and means to copy the f
function down but where ever you see an x, substitute in
the g function.
f x   2 x  3
2
g x   4 x  1
3
f  g  24 x  1  3
3
2
FOIL first and
then distribute
the 2
 32 x  16 x  2  3  32 x  16 x  5
6
3
6
3
12
g  f x  g f x
This is read “g composition f” and means to copy the g
function down but where ever you see an x, substitute in
the f function.
f x   2 x  3
g x   4 x  1
2
3
g  f  42 x  3  1
2
3
You could multiply
this out but since it’s
to the 3rd power we
won’t
12
 f  f x  f  f x
This is read “f composition f” and means to copy the f
function down but where ever you see an x, substitute in
the f function. (So sub the function into itself).
f x   2 x  3
g x   4 x  1
2
3
f  f  22 x  3  3
2
2
12
The DOMAIN of the
Composition Function
The domain of f composition g is the set of all numbers x
in the domain of g such that g(x) is in the domain of f.
f g 
1
f x  
x
1
g x   x  1
The domain of g is x  1
x  1 domain of f  g is x   : x  1
We also have to worry about any “illegals” in this composition
function, specifically dividing by 0. This would mean that x  1 so the
domain of the composition would be combining the two restrictions.
12
3.7 Homework Answers
1. f (3)  g (3)  6  9  15
3.
f (3)  g (3)  6(9)  54
f ( x)  g ( x)  3x 2  1
f (3)  g (3)  6  9  3
15.
f (3) 6 2
 
g (3) 9 3
f ( x)  g ( x)  3  x 2
5. f ( x)  g ( x)  2 x 4  3x 2  2
f ( x)  g ( x)  2 x  5
9.
11.
13.
f ( x)  g ( x)  x  5
f ( x) x 2  2 17.

g ( x) 2 x 2  1
f ( x)  g ( x)  0
f ( x)
1
g ( x)
h( x )  8 x  2 x  5 k ( x )  4 x  6 x  9
h(2)  31 k (3)  45
2
2
h( x)  8x3  20 x k ( x)  128x3  20 x
h(2)  24 k (3)  3396
19. h( x)  7
k ( x)  7 h(2)  7 k (3)  7
21. All R’s such that x>=-2
Domain:
f ( f ( x))  (4 x  2)  1 g ( g ( x))  ( x 4 )
(x<=1) or (x>=2)
h( x )  6 x  9
k ( x)  6 x  8
35.
f ( g ( x))  2 x 2  1
g ( f ( x))  (4 x 2  4 x  1)
h(2)  3 k (3)  10
x  3 2
h( x)  75 x 2  4 k ( x)  15 x 2  20
37. f(g(6))=5, g(f(6))=6, f(f(6))=6, and
h(2)  304 k (3)  155
g(g(6))=5
12
3.8 One-to-One Functions;
Inverse Function
12
A function f is one-to-one if for each x in the
domain of f there is exactly one y in the range and
no y in the range is the image of more than one x
in the domain.
A function is not one-to-one if two different
elements in the domain correspond to the same
element in the range.
12
x1
y1
x2
x3
y2
Domain
Range
x1
y1
x2
x3
y3
y3
Domain
One-to-one
function
x1
x3
Domain
Range
NOT One-to-one
function
y1
y2
y3
Range
Not a
function
13
M: Mother Function is NOT one-one
Joe
Samantha
Laura
Anna
Julie
Ian
Hilary
Chelsea
Barbara
George
Sue
Humans
Mothers
13
S: Social Security function IS one-one
Joe
123456789
Samantha
223456789
Anna
333456789
Ian
433456789
Chelsea
533456789
George
633456789
Americans
SSN
13
Is the function f below one – one?
1
10
2
11
3
12
4
13
5
14
6
15
7
16
13
Theorem Horizontal Line Test
If horizontal lines intersect the
graph of a function f in at most
one point, then f is one-to-one.
13
Use the graph to determine whether
2
the function f ( x )  2 x  5 x  1
is one-to-one.
Not one-to-one.
13
Use the graph to determine whether the
is one-to-one.
function
One-to-one.
13
The inverse of a one-one function is
obtained by switching the role of x and y
13
S
1
The inverse of the social security function
123456789
Joe
223456789
Samantha
333456789
Anna
433456789
Ian
533456789
Chelsea
633456789
George
SSN
Americans
13
Let f denote a one-to-one function y = f(x).
.
The inverse of f, denoted by f -1 , is a
function such that f -1(f( x )) = x for every x
in the domain of f and f(f -1(x))=x for every x
in the domain of f -1.
13
Theorem
The graph of a function f and the
1
graph of its inverse f are symmetric
with respect to the line y = x.
14
y=x
f
6
4
f
(0, 2)
1
2
(2, 0)
2
0
2
4
6
2
14
Finding the inverse of a 1-1 function
Step1: Write the equation in the form
y  f (x)
Step2: Interchange x and y.
Step 3: Solve for y.
Step 4: Write
for y.
f 1 ( x)
14
Find the inverse of
Step1:
5
f ( x) 
x 3
5
y
x3
Step2: Interchange x and y
Step 3: Solve for y
5
x
y 3
14
5  3x
f ( x) 
x
1
14
14
14
3.9 Direct & Inverse Variation
14
Example 1.
If W varies directly with F and when W = 24 , F = 6 . Find the
value W when F = 10.
W  4F
Solution.
W

F
W  kF
When W = 24, F = 6
 24  k 6
When F = 10 W = ?
W  4 10
W  40
k 6  24
k 4
14
Example 2.
If g varies directly with the square of h and when g = 100 ,
h = 5 . Find the value h when g = 64.
g  4h
Solution.
g h
2
g  kh
When g = 64 , h = ?
2
When g = 100 , h = 5
100  k 25
k 25  100
k4
2
64  4h 2
4h2  64
h 2  16
h  16
h = 4 or h = - 4
14
Example 3.
If d varies inversely with w and when d = 3 , w = 9 . Find
the value d when w = 3.
Solution.
1
d
w
k
d
w
27
d
w
When w = 3 d = ?
27
d
3
When d = 3 , w = 9
k
3
9
d=9
k = 27
15
Example 4 .
If r varies inversely with the square root of f and when
r = 32 , f = 16. Find f when r = 32.
Solution.
r
1
f
r
k
f
When r = 32 , f= 16.
k
16
32 
32 
k
4
k = 128
128
r
f
When r = 32 , f = ?
32 
128
f
32 f  128
128
f 
32
f 4
f  16
15
Example 5 .
If t varies jointly with m and b and t = 80 when
and b = 5. Find t when m = 5 and b = 8 .
Solution.
t  mb
m=2
t  8mb
When m = 5 , b = 8 , t = ?
t  kmb
t  8 5 8
When t = 80 , m = 2 and b = 5
t  320
80  k  2  5
10k  80
k 8
15
Example 6 .
c varies directly with the square of m and inversely with w.
c = 9 when m = 6 and w = 2 . Find c when m = 10 and
w=4.
Solution.
m2
c
w
c
km 2
w
When c = 9 , m = 6 and w = 2
9
k 62
2
36k 9

2
1
K=½
m2
c
2w
When m = 10 , w = 4
and c = ?
10 2
=12.5
c
2 4
15
Examination Questions.
Example 1.
The time,T minutes ,taken for a stadium to empty varies
directly as the number of spectators , S, and inversely
as the number of open exits, E.
(a) Write down a relationship connecting T,S and E.
It takes 12 minutes for a stadium to empty when there are
20 000 spectators and 20 open exits.
(b) How long does it take the stadium to empty when there
are 36 000 spectators and 24 open exits ?
15
Solution.
6S
T
500 E
(a) T S
E
K S
T
E
K is the constant of variation.
Now S = 36 000
and E = 24 .
(b)
6  36000
T
500  24
T = 12 , S = 20 000 and E = 20
Substitute to find the value of K.
12 K 20000

1
20
Cross multiply.
Substitute.
T = 18 minutes
20 000 K = 20 x 12
240
6
K

20000 500
15
Example 2.
The number of letters, N , which can be typed on a sheet
of paper varies inversely as the square of the size, S , of
the letters used.
(a) Write down a relationship connecting N and S .
(b) The size of the letters used is doubled.
What effect does this have on the number of letters which
can be typed on the sheet of paper ?
Solution.
(a)
(b)
Letter size = 2S
1
N 2
S
K
N 
(2 S )2
K
N 2
S
N
K
4S 2
By doubling the
size of letters
the number of
letters is
quartered.
15
Example 3.
A frictional force is necessary for a car to round a bend.
The frictional force , F kilonewtons , varies directly as the
square of the car’s speed , V metres per second, and inversely
as the radius of the bend, R metres.
(a) Write down a relationship between F, V and R.
A frictional force of 20 kilonewtons is necessary for
a car , travelling at a given speed , to round a bend.
(b) Find the frictional force necessary for the same
car , travelling at twice the given speed , to round the
same bend.
15
Solution.
(a)
V2
F
R
KV 2
F
R
(b)
Let the speed = 2V
K ( 2V )2
F 
R
4 KV 2
F
R
By doubling the speed
the frictional force F
required to round the
bend becomes 4 times
greater.
F = 4 x 20 = 80
K 4V 2
F 
R
15
3.9 Homework Answers
1.
3.
u  kv
12  k (30)
2
k
5
s
rk
t
5. k  14
13. (a) p  kd
(b) 118  k (2) k  59
(c) p  (59)5  295
k (2)
7
4
kx2
k (25)
k 3
25 
3
27
7.
k  27
z  kx2 y 3 16  k (49) (8)
9.
2
k
49
11. y  kx 16  k (4)
z2
9
k  36
y
k x
z3
5
k (3)
8
k
40
3
kl
R 2
d k (100)
15. (a)
(b) 25  (.01)
(c) 50
2
k
1
4000
9
17. (a) p  k
(b) 1.5  k
(c) 3
2
l
2
k
3
2
4
3
15
Ch. 3 Quiz Review Answers
Ch. 3 Test Packet Answers