Download Algebra 1 Things to Know for SOL Factoring: find 2 #`s add to 4, multi

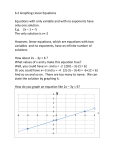
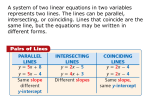
Algebra 1
Things to Know for SOL
Factoring: x  4 x  3
find 2 #’s add to 4, multi. to 3
( x  1)( x  3) factored
2
Absolute Value:
5  5
5 5
Represents distance
Radicals
√𝑥 4 = x2 (Divide
exponent by 2 bring
outside square root)
Exponents:
 3 
2
 3
n
mn
n m
 xn m
x x x
2
m
20  1
x 
1
43  3
4
1
n 1 
n
xm
 x mn
n
x
 xy 
n
 xn y n
 x  3 x  2  x x  x 2  3 x  3 2
 x2  5x  6
Divide:
𝟒𝒙𝟐
𝟐𝒙
1
= 2x or 2x
(Divide your coefficients, subtract exponents
Undefined slope:
X = 4 ; Vertical line (Slope = undefined)
Y = 4 : Horizontal line (Slope = 0)
Identity:
a  b  c   ab  ac
a0  a
Inverse:
a   a   0
Distributive Property:
Zero Property
√𝑥 5 =√𝑥 4 ∗ 𝑥 = x2 √𝑥
(List perfect squares for
integers, and simplify)
Graphing Inequalities:
< , > sign = Dotted line
≤ ≥ sign = solid line
(x,y)
Test Point (0,0) to find shading
If (0,0) makes true statement shade TOWARDS
(0,0) False-Shade away from (0,0)
Multiply: (distribute or FOIL)
Properties of Real Numbers:
Commutative Properties: a  b  b  a
ab  ba
Associative Properties: a   b  c    a  b   c a  bc    ab  c
Variations:
Direct y  mx where m = constant of
𝑦
𝑥
variation
(m = ) (Tables)
Inverse y 
m
x
(m = xy) (Tables)
Factor:
Look for the GCF (greatest common
factor first) 2x2 +8x + 6 = 2(x2 +4x + 3)
= 2(x+3)(x+1)
Equations of a Lines:
y  mx  b slope intercept
m = slope, b = y-intercept
y  y1  m  x  x1  point-slope
Systems:
y  2 x  1 Linear: Solution is where the
lines y  2 x  9 are equal or intersect.
to solve: substitution, elimination
Graph – ordered pair where lines
intersect
a 1 a
1
a 1
a
a 00
Degree :
Degree of monomial = sum of exponents
4x 3 is a degree of 3
Degree of Polynomial = degree of highest monomial degree
x 2  3x  1 is a degree of 2
Solving Equations:
1. Deal with any parentheses in the problem
2. Combine similar terms on same side of = sign
3. Get the needed variables on the same side of = sign
4. Isolate the needed variable by add or subtract
5. Find the needed variable by divide or multiply
Solve Quadratic Equations:
Parabola:
2
x  5x  6  0
Set = 0
y  ax 2  bx  c
 x  3 x  2  0 Factor
Roots, Solutions,
x  3  0, x  2  0 Set both factors = 0
Zeros, x-intercepts:
x  3, x  2
Find roots (solve)
Where the graph
Solve Quadratic Equations: Quadratic
crosses the x-axis.
Put in standard form: Ax 2  Bx  C  0
Equation.
b  b2  4ac
2a
2
3 x  2 x  7  0 , A = 3, B =  2, C = 7
x
Slope:
m
vertical change
rise y2  y1


horizontal change run x2  x1
Inequalities:
Remember to
5  3x  13  x
change direction
3x  8  x
of inequality when
4x  8
multiply/divide
by a negative
x  2
Function: Passes the vertical line test.
A set of ordered pairs in which each x
element has only one y element
associated with it.
f  x   3x  4
f  2  3  2  4  2
X and Y-intercept:
X-intercept: plug in 0 for Y, solve for X
Y-intercept: plug in 0 for X, solve for Y
Combine Like Terms:
must be same variable(s) and exponents,
combine the number in front
4 x 2  3  x 2  6  3x 2  9
Perimeter: add the distance around the outside
Area Rectangle: multiply the length and width
Box-and-Whisker Plot:
25%
25%
Minimum Q1
Statistics:
Mean = average = x = 
Standard Deviation = 
z score =
25%
Median
Q3
25%
Maximum
z
x

Parallel and Perpendicular Line:
Parallel: slopes are equal.
Perpendicular: slopes are negative reciprocal
(flip over and negate)
Statistics:
MAD = Mean Absolute Deviation
|𝑵𝒖𝒎𝒃𝒆𝒓 − 𝑴𝒆𝒂𝒏| for each element in data set
(Always Positive from absolute value)
= or
element  mean
standard deviation
Find the mean of those values
measures how many standard deviations
from the mean the observed values is.
Calculator
Graphing Functions
Y = to graph a lines or parabolas, must solve equations for y first
ZOOM 6: ZStandard (for normal window)
9: ZoomStat (to fit graph)
TRACE to put a curser on the graph
2nd TRACE CALC 2: zero (to find x intercept, zero, solution, root)
3: minimum (to find the lowest value, vertex of parabola)
4: maximum (to find the highest value, vertex of parabola)
5: intersect (to find point where two lines cross, solution)
Statistics
STAT for scatter plots and data sets
1: Edit to enter data into L1 , L2
→ CALC (for mean, standard deviation, line of best fit, curve best fit)
1: 1 – Var Stats (for mean, standard deviation)
2: LinReg(ax+b) (for line of best fit)
3: QuadReg for curve of best fit
Convert: decimal to fraction
MATH 1: Frac ENTER ENTER
Raise a number to an exponent
45 4  5
Clear the Calculator:
2nd + MEM 7: Reset… 1: All Ram ... 2: Reset
2nd + MEM 7: Reset… 2: Defalts … 2: Reset