Download Surveying Introduction

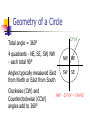
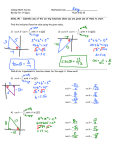
ENG 200 - Surveying


Ron Williams
Website:
http://web.mnstate.edu/RonWilliams
Surveying
The art of determining or establishing
the relative positions of points
on, above, or below the earth’s surface
Determining or Establishing



Determining: both points already exist determine their relative locations.
Establishing: one point, and the location of
another point relative to the first, are known.
Find the position and mark it.
Most property surveys are re-surveys


determining
you have no right to establish the corners
History of Surveying

First References




Dueteronomy 19:14
Code of Hannarubi
Egyptions used surveying
in 1400 b.c. to divide
land up for taxation
Romans introduced
surveying instruments
Surveying in America




Washington, Jefferson, and Lincoln were
survyors
The presence of surveyors meant someone
wanted land - often traveled with soldiers
Railroads opened up the country, but
surveyors led the railroad
East coast lands were divided by “Metes and
Bounds”, the west by US Public Lands
Types of Surveys

Plane Surveys


Assume NS lines are
parallel
Assume EW lines are
straight
Geodetic Surveys
Allow for convergence
Treat EW lines as great
circles
Used for large surveys
N
N
Types of Surveys




Land - define
boundaries of property
Topographic - mapping
surface features
Route - set corridors for
roads, etc.
City - lots and blocks,
sewer and water, etc.



Construction - line and
grade for building
Hydrographic - contours
and banks of lakes and
rivers
Mines - determine the
relative position of
shafts beneath the
earth’s surface
Safety Issues






Sun
Insects
Traffic
Brush cutting
Electrical lines
Property
owners
Units of Measure

Feet





Meters



Inches, 1/4, 1/8, etc.
1/10, 1/100, etc.
10’ 4-5/8” = 10.39’
Measure to nearest .01’
1 foot = 0.305 m
1 m = 3.28’
Stations
Units of Measure
Rods - 16.5 ft
Chains - 66 feet
4 rods = chain
Miles - 5280 feet
80 chains = 1 mile
320 rods = 1 mile
Others
Math Requirements




Degrees, Minutes, Seconds
Geometry of Circles
Trig Functions
Geometry, Trig of Triangles
° - ‘ - “ to Decimal Degrees

32°15’24”





1 degree = 60 minutes
1 minute = 60 seconds
24” = 24/60’ = 0.4’
15’24” = 15.4’
= 15.4/60° = 0.2567°
32°15’24” = 32.2567°
Most calculators do trig
calculations using decimal
degrees - CONVERT!
Decimal Degrees to DMS

 = 23.1248°




23.1248° = 23°7’29.3”
Watch roundoff!



0.1248*60 = 7.488 minutes
0.488*60 = 29.3 seconds
23.1° = 23°6’00”
We do most work to at least 1 minute!
Cheap scientific calculator - $12.00
Geometry of a Circle
23°18’
Total angle = 360°
4 quadrants - NE, SE, SW, NW
- each total 90°
Angles typically measured East
from North or East from South
Clockwise (CW) and
Counterclockwise (CCW)
angles add to 360°
NW
NE
SW
SE
360° - 23°18’ = 336°42’
Geometry of a Circle



Transit sited along line AB, 105°15’
clockwise from North.
C
Transit is turned 135°42’
counterclockwise to site on C.
Determine the direction of line AC.
 105°15’ - 135°42’ = -30°27’
N
135°42’
 Counterclockwise – angle gets smaller
 Negative result – add 360
 -30°27’ + 360° = 329°33’
 Or: 360° - 135°42’ = 224°18’
 105°15’ + 224°18’ = 329°33’
105°15’
A
B
224°18’
Trig Functions

Sin, Cos, Tan are ratios relating
the sides of right triangles

o - side opposite the angle
a - side adjacent to the angle

h - hypotenuse of triangle

hh
o

Sin  = o/h
Cos  = a/h

Tan  = o/a


aaa
Using Trig Functions
 Line AB bears 72°14’ East of North
 Length of AB, lAB = 375.46’
 Determine how far North and
how far East B is from A
 Cos = a/h, a = h*Cos
 NB/A = lAB * Cos(72°14’)
= 115.15’
 Sin = o/h; o = h*Sin
 EB/A = lAB * Sin(72°14’)
= 357.37’
357.37
115.15’
A
72°14’
375.46’
B
Triangle Geometry, Trig Laws


Sum of interior angles = 180°
Sine law:



A
B
C


sin  sin  sin 

if A = B,  = 
A
B
Cosine law:


A  B  C  2BC cos
2
2
if  = 90°, A2 = B2 + C2


C