Download CH6 Section 6.1

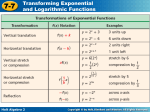
Chapter 6
Exponential and Logarithmic Functions
and Applications
Section 6.1
Section 6.1
Exponential Functions and Their Graphs
• Exponential Functions: Definition, Characteristics, and Graphs
• Transformations of Graphs of Exponential Functions
• Introduction to Exponential Growth and Decay
• Average Rate of Change
• Different Time Periods
• Increasing or Decreasing by a Constant Percent
• Comparing Linear and Exponential Growth
• Applications
Exponential Function
An exponential function is one of the form f(x) = bx , where
b and x are real numbers. Constant b is the base of the
function, b > 0, and b  1; variable x is the exponent.
The domain of f(x) = bx is the set of all real numbers.
The following are examples of exponential functions:
f(x) = 5x + 3
f(x) = –3x
f(x) = 8–x
f(x)   6 
x
The following are not exponential functions:
f(x) = x5 + 3
f(x) = (–3)x
f(x) = 0x
f(x) = 1x
Note: f(x)= –3x is not the same as f(x) = (–3)x. The latter one is
not exponential because the base is negative, b = –3. Observe
that the first one, f(x) = –3x, is obtained by multiplying f(x)= 3x by
–1, and it is exponential.
Graphing Exponential Functions
For each function, complete the table and graph the function:
f(x) = 3x
f(x) = (1/3)x
x
yy==33x x
x x
xx y =y(1/3)
= (1/3)
–2
3–2 = 1/9
–2
–2
(1/3) –2 = 9
–1
3–1 = 1/3
–1
–1
(1/3) –1 = 3
0
30 = 1
00
(1/3)0 = 1
1
31 = 3
11
(1/3)1 = 1/3
2
32 = 9
22
(1/3)2 = 1/9
Comparing Graphs
Both graphs have the same domain and range:
Domain = (–∞, ∞); Range = (0, ∞)
The y-intercept is (0, 1).
The x-axis is a horizontal asymptote.
Both are one-to-one functions.
f(x) = 3x, with b > 1, is increasing.
f(x) = (1/3)x, with 0 < b < 1, is decreasing.
Graphs of Exponential Functions
For the exponential function f(x) = bx, where b and x are
real numbers, b > 0, and b  1:
 The domain is the set of all real numbers, or (–∞, ∞),
and the range is the set of all positive real numbers,
or (0, ∞).
 The y-intercept is (0, 1).
 The x-axis (that is, the line y = 0) is a horizontal
asymptote.
 The function is one-to-one.
(continued on the next slide)
Graphs of Exponential Functions (contd.)
 The graph has one of the following shapes:
 If b > 1, the function is increasing; the larger the value of
b, the steeper the increase.
 If 0 < b < 1, the function is decreasing; the smaller the
value of b, the faster the decrease.
Transformations of Graphs of Exponential Functions (I)
Apply transformations to the graph of f(x) = 3x to construct the
graph of each function. Determine the horizontal asymptote and
the y-intercept for each function.
a. f(x) = 3x + 2
b. f(x) = 3x – 2
a. Vertical shift, up 2 units
Horizontal asymptote: y = 2
y-intercept from graph: (0, 3)
Verifying y-intercept:
f(0) = 30 + 2 = 1 + 2 = 3
b. Vertical shift, down 2 units
Horizontal asymptote: y = –2
y-intercept from graph: (0, –1)
Verifying y-intercept:
f(0) = 30 – 2 = 1 – 2 = –1
Transformations of Graphs of Exponential Functions (II)
Apply transformations to the graph of f(x) = 3x to construct the
graph of each function. Determine the horizontal asymptote and
the y-intercept for each function.
a. f(x) = 3x+2
b. f(x) = 3x–2
a. Horizontal shift, left 2 units
Horizontal asymptote: y = 0
y-intercept from graph: (0, 9)
Verifying y-intercept:
f(0) = 30+2 = 32 = 9
b. Horizontal shift, right 2 units
Horizontal asymptote: y = 0
y-intercept from graph: (0, 1/9)
Verifying y-intercept:
f(0) = 30–2 = 3–2 = 1/9
Transformations of Graphs of Exponential Functions (III)
Apply transformations to the graph of f(x) = 3x to construct the graph
of each function. Determine the horizontal asymptote and the
y-intercept for each function.
a. f(x) = –3x
b. f(x) = 3–x
a. Reflection about the x-axis
Horizontal asymptote: y = 0
y-intercept from graph: (0, –1)
Verifying y-intercept:
f(0) = –(30) = –1
b. Reflection about the y-axis
Horizontal asymptote: y = 0
y-intercept from graph: (0, 1)
Verifying y-intercept:
f(0) = 3–(0) = 1
Effect of Multiplying f(x) = bx by a Constant c
 If the exponential function of the form f(x) = bx is
multiplied by a constant c, where |c| > 1, the graph will be
stretched by a factor equivalent to the constant.
 If the exponential function of the form f(x) = bx is
multiplied by a constant c, where 0 < |c| < 1, the graph
will be compressed by a factor equivalent to the constant.
 The y-intercept of f(x) = cbx is (0, c).
Graph f(x) = 4(3x) and compare it to the graph of f(x) = 3x.
The graph of f(x) = 3x has been vertically stretched by a factor
of 4.
Both graphs have the same horizontal asymptote: y = 0
The y-intercept of f(x) = 4(3x) is (0, 4); the y-coordinate
corresponds to the value of the factor c = 4.
Verifying y-intercept: f(0) = 4(30) = 4(1) = 4
Graph f(x) = (1/4)(3x) and compare it to the graph of f(x) = 3x.
The graph of f(x) = 3x has been vertically compressed by a
factor of 1/4.
Both graphs have the same horizontal asymptote: y = 0
The y-intercept of f(x) = (1/4)(3x) is (0, 1/4); the y-coordinate
corresponds to the value of the factor c = 1/4.
Verifying y-intercept: f(0) = (1/4)(30) = (1/4)(1) = 1/4
Without graphing nor performing calculations, determine if
the function f(x) = 8(1.7)x is increasing or decreasing, and
find its vertical intercept.
The base of the exponential function is b = 1.7
Since b > 1, this function is increasing.
The y-intercept of an exponential function of the form
f(x) = cbx is (0, c).
Since c = 8, the vertical intercept is (0, 8).
Find the exponential function whose graph is shown below.
We are looking for an increasing exponential function f(x) = cbx.
Since the y-intercept is (0, 1), c = 1.
The point (2, 7.84) lies on its graph, thus we know that
f(2) = 7.84, and we look for a base b such that b2 = 7.84.
b2  7.84
b   7.84  2.8
Since the base cannot be negative, b = 2.8.
The exponential function is f(x) = 2.8x.
Find the exponential function whose graph is shown below.
We are looking for a decreasing exponential function f(x) = cbx.
Since the y-intercept is (0, 3), c = 3.
The point (3, 1.536) lies on its graph, thus we know that
f(3) = 1.536, and we look for a base b such that 3b3 = 1.536.
3b3  1.536
b3  0.512
b  3 0.512  0.8
The exponential function is f(x) = 3(0.8)x.
Basic Exponential Growth and Decay
The basic exponential growth and decay function is
given by:
P(t) = P0bt
where:
t = time
P0 = P(0) = the initial amount, or value of P at time 0;
P>0
b = growth factor if b > 1; decay factor if 0 < b < 1
The following table displays values for an exponential function.
Determine whether the function represents exponential growth
or decay. Find the growth or decay factor; complete the table.
t
0
P(t)
2
1
2
128
3
4
5
8162
As the t-values increase, the values of P(t) increase very fast.
This is an example of an exponential growth model. From the
table, we can see that P(0) = 2. So, we have P(t) = 2bt.
To find the value of the growth factor, b, we will choose any
given point - other than the initial value - and replace t and P(t)
accordingly, then solve for b.
(continued on the next slide)
(Contd.)
t
0
P(t)
2
1
2
3
128
4
5
8,162
Using the coordinates (2, 128), we can find the value of b in
P(t) = 2bt.
2b2 = 128
b2 = 64
b=8
The growth factor is b = 8, and the function is P(t) = 2(8)t.
The complete table is shown next.
t
0
1
2
3
4
5
P(t)
2
16
128
1024
8,162
65,53
6
As of 2014, Facebook was considered the world’s largest social
network. The number of Facebook active users in millions
through 2010 can be modeled by the function P(t) = 1.53(2.82)t,
where t is the number of years after 2004. Sources: www.facebook.com;
www.crunchbase.com, www.bizma.com
a. Identify the value of P0 and the growth or decay factor.
P(t) = 1.53(2.82)t . Therefore, P0 = 1.53 and b = 2.82.
Since the base is greater than 1, b = 2.82 is the growth factor.
b. Without graphing, determine whether the function is
increasing or decreasing. Explain your decision.
The function is increasing because b > 1.
(continued on the next slide)
(Contd.)
As of 2014, Facebook was considered the world’s largest social
network. The number of Facebook active users in millions
through 2010 can be modeled by the function P(t) = 1.53(2.82)t,
where t is the number of years after 2004. Sources: www.facebook.com;
www.crunchbase.com, www.bizma.com
c. Graph the function with your calculator. Label the axes and
show your viewing window. Identify and interpret the vertical
intercept.
Active users
Year
[0, 10, 1] by [0, 550, 50]
The vertical intercept in P(t) = 1.53(2.82)t is (0,1.53), which
approximates the number of active users (in millions) in 2004.
(continued on the next slide)
(Contd.)
d. Approximate the number of Facebook active users in 2008.
Find the answer graphically, numerically, and algebraically.
Round your answer to the nearest whole number
In 2008, there were approximately 97 million Facebook active
users, as demonstrated next.
Graphically
Numerically
Algebraically
P(4) = 1.53(2.82)4 = 96.76  97
Average Rate of Change
Recall that if (x1, f(x1)) and (x2, f(x2)) represent two distinct points
on the graph of a function f, the average rate of change of f
between x1 and x2 is given by
y f ( x 2 )  f ( x1 )

x
x 2  x1
Using the data from the previous problem, find the average rate
of change in the number of Facebook active users between
2006 and 2008. Round to the nearest whole number.
For 2006, x = 2. So, P(2) = 1.53(2.82)2 = 12.17
For 2008, x = 4. So, P(4) = 1.53(2.82)4 = 96.76
y 96.76  12.17

 42.3  42
x
42
The average rate of change in the number of Facebook active
users between 2006-2008 was 42 million.
Different Time Periods
If an exponential problem states that the growth or decay
factor b occurs at a fixed time period, like every year,
month, week, day, hour, etc., we can use P(t) = P0bt for
time t.
If the problem refers to a different time period, such as
every 3 days, every 5 months, every 2 years etc., then we
need to adjust the time exponent accordingly.
Hint: Think of “every n amount of time” as t/n.
For example, every 3 days would be reflected as t/3,
every 5 months, t/5, etc.
Increasing or Decreasing by a Constant Percent
For an exponential growth or decay model P(t) = P0bt:
 If b > 1, the growth rate satisfies b = 1 + r, where r is the
percent increase.
Example:
If a quantity grows by 2%, the growth rate is 0.02, therefore,
b = 1 + 0.02 = 1.02.
If 0 < b < 1, the decay rate satisfies b = 1 – r, where r is
the percent decrease.
Example:
If a quantity decays by 2%, the decay rate is 0.02, therefore,
b = 1 – 0.02 = 0.98.
Suppose that a particular bacteria culture initially contained 500
bacteria and they increased by 25% every 3 weeks.
a. Write an exponential function N(t) that models this problem
for t weeks.
N(t) = 500(1.25)t/3
b. Determine the number of bacteria after 6 weeks. Round your
answer to the nearest whole number.
N(6) = 500(1.25)6/3 = 500(1.25)2  781 bacteria
c. Determine the number of bacteria after 5 months. Round to
the nearest whole number. (Assume 4 weeks per month.)
For 5 months, t = 20.
N(20) = 500(1.25)20/3  2213 bacteria
Caution: Remember to enclose the exponent “20/3” within a set of
parentheses when performing calculations with the calculator.
Comparing Linear and Exponential Growth
Compare the linear function f(x) = 2 + 3x and the exponential
function g(x) = 2(3)x for 0  x  5.
x
f(x) = 2 + 3x
g(x) = 2(3)x
0 2 + 3(0) = 2
2(3)0 = 2
1 2 + 3(1) = 5
2(3)1 = 6
2 2 + 3(2) = 8
2(3)2 = 18
3 2 + 3(3) = 11 2(3)3 = 54
4 2 + 3(4) = 14 2(3)4 =162
The output values for the exponential function grow much faster.
Increasing the x-values by one in the linear function has the effect
of adding 3 more units to the value of f(x), whereas increasing the
x-values by one in the exponential function has the effect of
multiplying g(x) by the growth factor 3 each time.
The average rate of change for a linear function is constant, while
the average rate of change of the exponential function is not.
A medical clinic has identified 2 cases of a new virus. Each
subsequent day, a new patient arrives with the same virus,
and four days later, the clinic has treated a total of 6 patients
who have contracted the virus.
a. Suppose that the number of patients with this virus grows
linearly. Write a function L(x) that models this problem, where
x represents days.
L(x) = 2 + x
b. Use your linear function to estimate how many patients will
contract the virus in 12 days.
L(12) = 2 + 12 = 14 patients
(continued on the next slide)
(Contd.)
c. Suppose that the number of patients with this virus grows
exponentially. Write a function E(x) that models this problem,
where x represents days.
The initial number of patients was 2. So, E(0) = 2, and we have
E(x) = 2bx.
During the 4th day, there were 6 cases, thus we can use the
point (4, 6) to find the growth factor, b.
6 = 2b4
3 = b4
(3)(1/4) = b
1.3161= b
Therefore, our function is E(x) = 2(1.361)x.
(continued on the next slide)
(Contd.)
d. Use your exponential function to estimate how many patients
will contract the virus after 12 days.
E(12) = 2(1.361)12 = 54 patients
e. Graph both functions with your calculator. Label the
axes and show your viewing window. Compare both growths.
Virus patients
Days
[0, 30, 5] by [0, 100, 20]
Both graphs are increasing and they confirm that the
exponential growth overruns the linear one.
Using your textbook, practice the
problems assigned by your instructor to
review the concepts from Section 6.1.