Download RECOUNT Lesson 4.2: Angle Relationships in Triangles Page 223

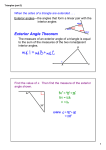
Lesson 4.2: Angle Relationships in Triangles
Page 223 in text
Learning Objectives:
The learner will be able to find the measures of interior and exterior angles of triangles
The learner will be able to apply theorems about the interior and exterior angles of triangles
The learner will understand and apply The Triangle Sum Theorem
The learner will understand the relationship between the exterior angle of a triangle and its two remote interior angles
Common Core Standards: Prove geometric theorems
G-CO.10. Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of
isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the
length; the medians of a triangle meet at a point.
Continuity:
Previous Lessons
Yesterday we learned how
to classify triangles
according to side length and
angle measure.
This Lesson
Today, we will prove that
the angle measures of a
triangle add up to 180
degrees, and we will prove
that the measure of an
exterior angle of a triangle is
equal to the sum of the two
nonadjacent angles of the
triangle
Next Lesson
Next, we’ll add to our
knowledge by exploring
congruence in the context of
triangles.
Lesson Overview
Opening: Hand back tests from Chapter 3
Launch: Warm Up



Review Angle Measures
Review Triangle Classifications
Review Interior and Exterior Angles
Explore:




Triangle Sum Activity
o Tearing triangles angles to show they add up to 180o
o Folding triangle into a rectangle to show angle sum is 180o
Triangle Sum Proof
o Corollaries
 What is a corollary anyways?
Exterior Angle Proof
o Why does this make sense?
o Reflect back to Triangle Sum Activity
Third Angles Theorem
Reflect: Exit Slip



How are the three main theorems we learned today connected?
What did you learn?
What are you still confused about?
Homework:

2-5, 6-14E, 24, 28,
THE PLAN! The lesson
stayed pretty true to this
format but we ran out of
time and the end and didn’t
get to reflect or complete
exit slips.
Detailed Outline
Warm UP
Objective
Activity
Recall Angle
Acute
Right
Obtuse
Measures to connect 0 < ∢𝐴 < 90
m  A = 90
90 < ∢𝐴 < 180
what learners know
about angles to what
they will learn about
classifying triangles
by angle measure.
Classify Triangles by (By Angles):
Angle Measure and
Acute
Right
Obtuse
Side Length by
3 acute  ’s
1 right 
1 obtuse 
identifying
(2 acute  ’s)
(2 acute  ’s)
properties and
attributes of the
figures.
(By Sides):
Scalene
No  sides
Isosceles
 2  sides
Equilateral
3  sides
Teacher
Timing
Straight
Use Effective
2 min
m  A = 180
Questioning
from PBS sheet.
The warm up was a struggle. It was
extremely hard for the class to recall
what they learned in chapter 3. The
warm up activity took a lot longer than I
visual on on 2 min
planned. They didn’tDraw
ask questions
Equiangular
board
Lesson 4.1 Homework but that
their inability
3 congruent  ’s looks like
to answer
questions
regarding
(all
acute 
’s)
picture
for triangle
classifications madelearners
it obvious
that
who
there was definitelyneed
confusion. The main
confusion seems to organization
be between sides
and
visual.
and angles. Since this information
is not
necessarily vital for today’s lesson I
should have added homework problems
that address triangle classification
instead of spending class time on it. The
parallel postulate warm ups served a
great purpose later in the lesson and
were worth the time.
Recall Parallel
Postulate
How many lines can be drawn through N parallel to ̅̅̅̅̅
𝑀𝑃 ?
N
M
P
Answer: Exactly 1 by the Parallel Postulate.
Review Exterior
and Interior Angles
Introduce
auxiliary line. If
learners cannot
recall have
them flip back
in their
textbook.
Have students
label all angle
relationships.
3 min
3 min
Dialogue for
Intro.
Proving
Triangles Sum
is 180 degrees.
This is clearly
something
we’ve known
and accepted
for awhile but
now we are
going to prove
it!
Objective of
Activity
Students will
“discover” or
convince themselves
that the Triangle
Sum Theorem
should in fact be
true.
Students will help
with the proof of the
Triangle Sum
Theorem (sketch of
the proof), thus
working on their
proof skills.
Explore
Part 1: Triangle Sum Theorem
Outline of Activity
Teacher
Have students (with partners) rip
corners of each triangle (each
type of triangle by angle) and line
them up on a straight line on
their paper (straight angle) –
have them make conjectures [the
interior angles in a triangle add
up to 180 degrees].
Sketch the proof for The Triangle
Sum Theorem – refer them to
Page 223 in their book to see the
full proof. Mentions use of
Auxiliary line.
***(SEE SKETCH BELOW)
Mentions corollary to the
Triangle Sum Theorem [in a right
triangle, the acute angles are
complementary] CHECK 2 in text
Sketches proof out loud with
students.
Timing
Assessment
Gives students a
15
Students will work
non-precise
minutes with partners to make
justification of
conjectures. They will
the Triangle Sum
make the correct
Theorem. Allows
conjecture, or if they
them to learn in a
make an incorrect
concrete, handsconjecture, this allows
on way.
me to target
Allows students
misconceptions.
to see the idea of
the proof, but
puts
responsibility on
them to discover
Since
the warm up activity took longer than
it. Once
they
anticipated
understand
the we had to rush through the paper
purpose,
they can activities. Learners enjoyed
tearing/folding
delvemaking
into thethe connection and it truly made the
formal proof and
proof run a lot smoother. Also, this activity was
really make
asidea
a class instead of in partners since we
sensedone
of the
short on time. It worked just as well in a
beingwere
discussed.
large group and I probably would implement it
as a large group again.
Sketch of Proof (with guided questing from teacher)
Triangle Sum Proof: With what we
know about parallel lines and
alternate interior angles, it's pretty
straight forward:
The warm up activity and triangle sum
activity really helped the learners develop
the triangle sum proof. Everything within
the triangle sum proof went as planned,
just a little faster. But, the activities
leading up to the proof helped learners
answer the questions which saved time.
Construct Auxiliary Line: a line that is added to a figure to aid in a proof.




How can we justify the auxiliary lines existence? That is, why are we allowed to
construct this line?
Through any two points there is exactly one line.
̅̅̅̅?
But how can we make our auxiliary parallel to AC
By the parallel postulate!!
What kind of Angles did we create? Label Interior and Exterior


What would the transversal be in each case?
Does this make sense in terms of the activity we did when we tore angles from the
triangles?
COROLLARIES for triangle sum theorem: What is a corollary anyways? A theorem
whose proof follows directly from another theorem. So basically, we get these for free, well
almost free.
CHECK 2 in text
Part 2: Exterior Angles Theorem
Dialogue for
Intro.
Part 2:
Exterior
Angles. In the
first activity we
were able to create
and examine the
features of a
triangle. In doing
this, we learned
how to use
deductive
reasoning to
formally prove the
sum of the
measures of the
interior angles is
equal to the
measure of a
straight angle
(180o) of a line
drawn through one
of the vertices. We
will now use that
information to
examine the
exterior angles of a
triangle.
Objective of Activity
Students will use
what they know to
help them sketch the
Exterior Angle
theorem. Students
will see why this
theorem seems
logical and then they
will formulate a
proof.
Outline of Activity
Recall what we know about
triangles
Define terms: remote interior
angles, exterior angles, and
interior angles.***See Definition
Whiteboard Activity BELOW
Read the Exterior Angles
Theorem from book on page 225.
Do CHECK 3 in book with
partners.
Teacher uses GEOGEBRA to
“convince them” in a non-precise
sense that the theorem is true.
Then sketch the proof for The
Exterior Angle Theorem on the
board– refer them to Page 225 in
their book to examples of the
Theorem. ***See Geogebra
sketch BELOW
Teacher
Timing
Assessment
Allows students
20 min
Students will be
to see visual
enthusiastic, or at least
representation of
engaged in watching
the material and
Geogebra. They will
build off prior
have ideas of how to
knowledge by
sketch the proof of this
connecting
theorem and will
familiar concepts
believe it to be true. If
Students
representation
with the
new loved the visualthe
students aren’t
would
give
ideas. here. If I could redo this lesson
askingI the
right
kinds
of
questions
or
are
them the opportunity to use Geogebra
Includes
applying
the wrong
instead of just watching me
do it. This
technology in the
vocabulary, I can stop
activity
helped visual learners
make
classroom
for the
the demonstration
and
connections,
but
I
seemed
to
be
doing
all
the
purpose of
review the main ideas
They would have liked
it better
makingwork.
a
we are
usingiftothey
conjecture.
the proof.
had the change to utilize construct
the technology
to
support their own understanding. It was
definitely worth implementing, though.
Interior and Exterior Angles in
Triangle
Whiteboard Organization
An interior angle is formed by two sides of a triangle.( inside the figure)

In figure: ∠1, ∠2, ∠3
An exterior angle is formed by one side of the triangle and the extension of the
adjacent side. (outside the figure)
CHECK 3




IN figure: ∠4
Each exterior angle has two remote interior angles.
In figure: ∠1 𝑎𝑛𝑑 ∠2
A remote interior angle is an interior angle that is not
adjacent to the exterior angle. (Interior and away from exterior)
The visuals and organization helped learners make
Exterior
Angle:
sense of the material. However,
in the
futureA Ibetter
wouldvisual of why the proof make sense
not prove the exterior angles theorem for them.
They are not assessed on their ability to prove this
theorem but rather employ it given a context. BY this
time the learners were done learning about proofs
and felt overwhelmed. Learning two big proofs in
one day was a lot for them. In the future I would
need to find some way to break up the big ideas, but
its hard because there is clearly a relationship.
Geometers Sketchpad Proof (tying everything back together)
Theorem: The measure of an exterior angle
of a triangle is equal to the sum of the
measures of its two remote interior angles.
Using Geogebra, try 2 examples to see if the
theorem is true.
In the figures above the exterior angle ∠ABP is equal to the sum of the remote interior angles ∠BAC and
∠ACB.
Now that the conjecture is believed to be
true, work through a formal proof with
students.
PART 3: Third Angles Theorem
Outline of Activity
Teacher
Dialogue for
Objective of
Intro.
Activity
Read the Third Angles Theorem
Next we are
The students will
going to look
understand how to
Aloud to the class.
at the Third
compare angles
Angles
amongst two
Let them work on CHECK 4 in the
Theorem. We triangles and will
text in partners.
will discuss
understand how to
The remaining
spent organizing
the angle
ideas of
during
why ittime
makes
find the third
Asthe
a class discuss our findings
lesson. I was
available
to
answer
questions.
A
lot
of
students
sense and how a triangle by applying and connections.
we can use
the previous
really understood
theit.concepts
and made connections, but
theorems.
they did stress that they felt overwhelmed- but in a good way.
Unfortunately, we ran out of time and the learners weren’t
able to fill out the exit slips. Summarizing and solidifying
understanding is one of the most important things, so next
time I need to better enforce my time management skills to
ensure that I leave time for reflection.
Reflection
Objective
Summarize lesson.
Complete Exit Slip
Apply
understanding to
homework.
Timing
Gives the
10 min
students freedom
to explore the
third theorem,
which is fairly
straightforward,
with one another.
Asks questions
that force the
learners to use
the exterior
angles theorem
and triangle sum
theorem.
Assessment
Students will be given
the freedom to explore
examples that force
them to apply all of the
theorems they learned
to find the third angle.
The teacher can walk
around and ask
questions to ensure
learners understand
the material.
The differentiated instruction
methods definitely helped keep
most learners engaged and gave
almost everyone the opportunity to
participate. Overall, the lesson was a
bit rushed Teacher
but it was okay. The
Activity
Timing
helped
memin
Today we learned how to classify triangles, we learned that the angle measures of a triangleinformal
add up assessments
Wraps up what 10
to 180 degrees, and we learned that the measure of an exterior angle of a triangle is equal to
the which
identify
was learners
covered.did not meet
sum of the two nonadjacent angles of the triangle. Now, it’s time to try some problems thatthe
apply
lesson Assesses
objectives and standards,
what you know from today’s lesson and from your previous experience with angles, side lengths,
student
although
almost the whole class did.
and triangles, to some homework problems. Tomorrow we’ll add to our knowledge of triangles
by
learning.
Next time I want to focus on my
exploring congruence in the context of triangles.
time management.
………
.