Download Systems of Linear Equations - Finite Mathematics Section 1.3

Section 1.3 – Systems of Linear Equations
A system of linear equations is a set of two or more linear equations. It is also called a linear
system.
In this section we will study 2×2 linear systems, which are systems that contain two equations
and two unknowns. The solution set to a linear system is the set of all ordered pairs that
satisfies all of the equations in the system.
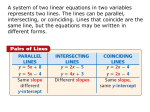
A linear system may have one solution, no solution or infinitely many solutions.
If a linear system has one solution, then the lines intersect at one point, and that point represents
the solution to the system. An illustration is shown below.
If a linear system has no solution, then the two lines never intersect and are therefore parallel. An
illustration is shown below.
If a linear system has infinitely many solutions, then the two lines coincide and represent the
same line. The solution set is represented by every point on the line, which is an infinite number
of points. An illustration is shown below.
Math 1313
Page 1 of 11
Section 1.3
In this textbook, each system of equations will be preceded by a single left curly brace, as shown
in the examples below. Not all textbooks follow this convention, but it is a way to group the
equations together and to quickly identify a system of equations.
Example 1: Determine whether ( −1, − 3) is a solution to the following system of equations.
 − y = x+4

 2 x + y = −6
Solution: To check if ( −1, − 3) , is a solution to the system, we substitute x = −1 and y = −3 into
each equation to determine if the point satisfies both equations.
−y = x + 4
2 x + y = −6
?
− ( −3 ) = − 1 + 4
?
2 ( −1) + ( −3) = − 6
3=3
?
−2 − 3 = − 6
−5 ≠ −6
Notice that the point satisfies the first equation, but not the second. Since ( −1, − 3) does not
satisfy both equations, the ordered pair is not a solution to the system.
***
Math 1313
Page 2 of 11
Section 1.3
 5

Example 2: Determine whether  − , 16  is a solution to the following system of equations.
 3

1

 3 x − 2 y = −13

 − 9 x + 3 y = 27

4
5
 5

Solution: To check if  − , 16  is a solution to the system, we substitute x = − and y = 16
3
 3

into each equation to determine if the point satisfies both equations.
3x −
1
y = −13
2
?
 5 1
3  −  − (16 ) = − 13
 3 2
?
−5 − 8 = − 13
−13 = −13
−9 x +
3
y = 27
4
?
 5 3
−9  −  + (16 ) = 27
 3 4
?
15 + 12 = 27
27 = 27
 5

Since  − , 16  satisfies both equations, it is a solution to the system.
 3

***
When solving a linear system, we are finding any points of intersection. Remember that two
lines either intersect in one point, or they are parallel and do not intersect at all, or they coincide
and intersect in infinitely many points. One method is to graph the lines and look for the
intersection, which works well when the x- and y-values of the point of intersection are integers,
and are reasonably close to the origin. In this section, we will instead focus on solving the system
algebraically. To do this, we can use either the substitution method or the elimination method.
You should be familiar with both of these methods.
Solving a Linear System Using the Substitution Method
Example 3: Solve the following system using the substitution method.
 y = x −1

 y = −x + 3
Math 1313
Page 3 of 11
Section 1.3
Solution: Notice that each equation is already solved for y. We can take the right hand side of
one equation, and substitute it into the other equation for y. This results in an equation in the
variable x:
y = x −1
− x + 3 = x −1
Now solve for x.
− x + 3 = x −1
−2 x = −4
x=2
The x-coordinate of the point of intersection is x = 2 .
To find the y-coordinate of the point of intersection, we now substitute x = 2 into either of the
two original equations, and solve for y. We only need to use one of the equations (as they yield
the same result), but both methods of solving for y are shown below.
y = x −1
y = 2 −1
y =1
y = −x + 3
or
y = −2 + 3
y =1
The y-coordinate of the point of intersection is y = 1 .
The solution to the linear system is ( 2, 1) .
***
Example 4: Solve the following system using the substitution method:
 − 3 x = 18 y + 3

 4 x + 5 y = 15
Solution: We first need to solve one equation for either x or y. We will choose to solve the first
equation for x:
−3 x = 18 y + 3
18 y + 3
18
3
=− y−
−3
3
3
x = −6 y − 1
x=
Math 1313
Page 4 of 11
Section 1.3
Next, we substitute x = −6 y − 1 into the second equation, 4 x + 5 y = 15 , and solve for y. (Notice
that we do not plug x = −6 y − 1 into the equation −3 x = 18 y + 3 , since they represent the same
equation.)
4 x + 5 y = 15
4 ( −6 y − 1) + 5 y = 15
−24 y − 4 + 5 y = 15
−19 y = 19
y = −1
The y-coordinate of the point of intersection is y = −1 . We now need to find the corresponding
x-value. To do this, we can plug y = −1 into either of the two original equations or into
x = −6 y − 1 . We will choose to use x = −6 y − 1 , since the equation is already solved for x.
x = −6 y − 1
x = −6 ( −1) − 1
x = 6 −1
x=5
The x-coordinate of the point of intersection is x = 5 .
The point of intersection of the two lines, or the solution to the linear system, is ( 5, − 1) . This
system of linear equations has only one solution.
***
Example 5: Solve the following system using the substitution method:
 −3 x + 2 y = 22

 − 15 x + 10 y = 1
Solution: We first need to solve one equation for either x or y. We will choose to solve the first
equation for y:
−3 x + 2 y = 22
2 y = 3 x + 22
3 x + 22 3
22
y=
= x+
2
2
2
3
y = x + 11
2
Math 1313
Page 5 of 11
Section 1.3
Now substitute y =
3
x + 11 into the second equation, −15 x + 10 y = 1 , and solve for x.
2
−15 x + 10 y = 1
3

−15 x + 10  x + 11 = 1
2

−15 x + 15 x + 110 = 1
110 = 1
The x terms cancel and we simply get 110 = 1 . This is never true, which indicates there is no
solution to the system. If we graphed these two lines, they would be parallel.
***
Solving a Linear System Using the Elimination Method
Example 6: Solve the following system using the elimination method:
 x − 11 y = 14

 x + 11 y = −2
Solution: We must first choose a variable to eliminate. Since the coefficients of the y-terms are
already opposites of each other (and add to zero), we add the two equations together to obtain
one equation in the variable x. We then solve that equation for x.
x − 11 y = 14
+ x + 11 y = −2
2x
= 12
x=6
Now substitute x = 6 back into either one of the original equations, and solve for y. We will use
the first equation:
x − 11 y = 14
6 − 11 y = 14
−11 y = 8
y=−
8
11
Math 1313
Page 6 of 11
Section 1.3
8

The solution to the linear system is  6, −  .
11 

***
Example 7: Solve the following system using the elimination method:
 4 x + 4 y = 36

 2x + 3 y = 8
Solution: We must first choose a variable to eliminate. Two different options are shown below.
Looking at the x-terms: The least common multiple of 4x and 2x is 4x . We could keep the first
equation the same so that it contains the term 4x , and multiply the second equation by −2 so
that it contains the term −4 x .
Looking at the y-terms: The least common multiple of 4 y and 3 y is 12 y . We could multiply
the first equation by 3 so that it contains the term 12 y , and multiply the second equation by −4
so that it contains the term −12 y .
We will choose to eliminate the x-terms. This minimizes our work, since we only need to
multiply one of the equations by a nonzero constant to make the coefficients of the x terms
opposites.
Multiply the second equation by −2 :
−2 ( 2 x + 3 y ) = −2 ( 8 )
−4 x − 6 y = −16
Now add the first equation to the revised second equation, and solve for y.
4 x + 4 y = 36
+ − 4 x − 6 y = −16
− 2 y = 20
y = −10
Math 1313
Page 7 of 11
Section 1.3
Next, we substitute y = −10 into either one of the original equations, and solve for x. We will
use the first equation:
4 x + 4 y = 36
4 x + 4 ( −10 ) = 36
4 x − 40 = 36
4 x = 76
x = 19
The solution to the linear system is (19, − 10 ) .
***
Example 8: Use the elimination method to find the x-coordinate of the point of intersection for
the following system:
 4 x − 3 y = −40

 − 5 x + 6 y = 59
Solution: We must first choose a variable to eliminate. Two different options are shown below.
Looking at the x-terms: The least common multiple of 4x and 5x is 20x . We could multiply the
first equation by 5 so that it contains the term 20x , and multiply the second equation by 4 so that
it contains the term −20x .
Looking at the y-terms: The least common multiple of 3y and 6 y is 6 y . We could multiply the
first equation by 2 so that it contains a −6 y . The second equation already contains the term 6 y .
We will choose to eliminate the y-terms for two reasons. First of all, we only need to multiply
one equation by a nonzero constant to make the coefficients of the y terms opposites. Also, we
are only asked to find the x-coordinate of the point of intersection, which we will be able to do
directly if we eliminate the y-terms.
Multiply the first equation by 2:
2 ( 4 x − 3 y ) = 2 ( −40 )
8 x − 6 y = −80
Math 1313
Page 8 of 11
Section 1.3
Now add the revised first equation to the second original equation, and solve for x.
8 x − 6 y = −80
+ − 5 x + 6 y = 59
3x
= −21
x = −7
The x-coordinate of the point of intersection is x = −7 . (Remember that we were only asked to
solve for x, so we do not need to solve for y.)
***
Example 9: Use the elimination method to find the y-coordinate of the point of intersection for
the following system:
 2 x + 8 y = −14

 3 x − 6 y = −3
Solution: We must first choose a variable to eliminate. Since we are asked to solve for y, we will
choose to eliminate the variable x.
The least common multiple of 2x and 3x is 6x . We can multiply the first equation by −3 so
that it contains the term −6x , and multiply the second equation by 2 so that it contains the term
6x .
−3 ( 2 x + 8 y ) = −3 ( −14 )
2 ( 3 x − 6 y ) = 2 ( −3)
We obtain the following equations:
−6 x − 24 y = 42
6 x − 12 y = −6
Now add the resulting equations and solve for y.
− 6 x − 24 y = 42
+
6 x − 12 y = −6
36 y = 36
y = −1
Math 1313
Page 9 of 11
Section 1.3
The y-coordinate of the point of intersection is y = −1 . (Remember that we were only asked to
solve for y, so we do not need to solve for x.)
***
Example 10: Use the elimination method to find the point of intersection for the following
system:
 − 2x + y = 5

 − 4 x + 2 y = 10
Solution: We must first choose a variable to eliminate. Let us choose to eliminate the variable y.
The least common multiple of y and 2 y is 2 y . Multiply the first equation by −2 :
−2 ( −2 x + y ) = −2 ( 5 )
4 x − 2 y = −10
Now add the revised first equation to the second original equation:
4 x − 2 y = −10
+ − 4 x + 2 y = 10
0 = 0
The x and y terms cancel and we simply get 0 = 0 . This statement is always true, which indicates
that the system has infinitely many solutions. If the two equations were graphed, it would be seen
that they both represent the same line.
Although there are infinitely many solutions, it is not correct to say that the solution is “All real
numbers.” While it is true that x can take on any value, the y-value needs to be chosen so that the
point falls on the line, and we can conversely choose any y-value, but then the x-value needs to
be chosen so that the point falls on the line.
The solution set to the given system is the set of all pairs ( x, y ) , where x and y are real numbers,
such that each ordered pair falls on the given line. We can write this in set-builder notation as
follows:
Set builder notation:
{ ( x , y ) | − 2x + y = 5 }
Translated in words: “The set of all points ( x, y ) such that −2 x + y = 5 .”
Math 1313
Page 10 of 11
Section 1.3
The form that the solution set is written in is not unique. Since −2 x + y = 5 and −4 x + 2 y = 10
represent the same line, we could have instead written the solution as:
Set builder notation:
{ ( x , y ) | − 4 x + 2 y = 10 }
Translated in words: “The set of all points ( x, y ) such that −4 x + 2 y = 10 .”
***
Math 1313
Page 11 of 11
Section 1.3