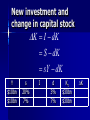Download Theories of Economic Growth

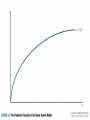
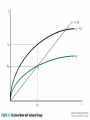
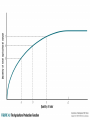
Chapter 4
Theories of
Economic
Growth
Five Equations





Aggregate production function
Saving function
Saving = Investment
Relation between new investment
and change in capital stock
Growth rate of labor
Aggregate production
function
Y  F ( K , L)


What is exactly the shape of the
function F ?
Where do K and L come from?
Saving function
S  s Y
Gross savings (% of GDP), 2005
Chile
China
Sierra Leone
Bolivia
18.9
50.4
7.6
20.4
Nigeria
India
30.5
32.7
Saving and Investment
SI


Assume no trade and no government
Or assume that
SS
private
S
gov
S
foreign
with “foreign saving” = capital inflows
New investment and
change in capital stock
Kt 1  Kt  K  I  dK

d = rate of depreciation
I
$2bn
$2bn
d
3%
7%
Kt
$30bn
$30bn
K
Kt+1
New investment and
change in capital stock
K  I  dK
 S  dK
 sY  dK
Y
$10bn
$10bn
s
20%
7%
I
d
3%
7%
Kt
$30bn
$30bn
K
Labor Force Growth
Lt 1  Lt  L  nL

n = rate of population growth
n
2%
4%
Lt
1mn
1mn
L
Lt+1
The Harrod-Domar Model
R. F. Harrod, The
Economic Journal,
Vol. 49, No. 193.
(Mar., 1939), pp.
14-33.
Econometric
a, Vol. 14,
No. 2. (Apr.,
1946), pp.
137-147
Fixed Coefficient
Production Function

Isoquants
– Combination of inputs that produce equal
amounts of output

Fixed coefficient production function
– Assume capital and labor have to be used
in constant proportions (i.e., 10 people
for every $1m of capital).
– What happens if you raise K, keeping L
constant?
Y=200,000*$50=$10,000,000
K/Y=$20,000,000/$10,000,000
=2
Fixed Coefficient
Production Function

Fixed coefficient production function
– K/L is constant if production is efficient
– Constant returns to scale

K/Y and L/Y are constant
The Harrod-Domar Model


Assume labor is unemployed
Capital is the binding constraint
K
Y
v
K
v
Y
K
ICOR  v 
Y
The Harrod-Domar Model

Capital-output ratio
– Capital intensity of production process
and of product
– Efficiency with which capital is used

Capital-output ratio versus
Incremental Capital-Output Ratio
– Assume average K/Y = ICOR
The Harrod-Domar Model
Y
K
Agriculture
$5bn
$1bn
Industry
$5bn
Services
v
10
$1bn
1
The Harrod-Domar Model
Y 
K
v
Y
K
K
v
g


Y
Y
Yv
The Harrod-Domar Model
g
Y
Y

K
Yv
Yv  K
K  sY  dK
sY  dK s
g
 d
Yv
v
The Harrod-Domar Model
s
g  d
v


Capital created by investment is the
main determinant of growth.
Saving makes investment possible
The Harrod-Domar Model
s
g  d
v
g
d
v
3%
5%
3%
5%
5%
27%
5%
24.4
(same as
above)
s
The Harrod-Domar Model

Consequences
– Saving as crucial for growth
– Knife-edge dynamics
If n>g (g=s/v-d), then chronic
unemployment
 If n<g
, then chronic labor
shortages, capital becomes idle

– No endogenous process to bring the
economy to equilibrium
The Harrod-Domar Model

Strengths
– Simplicity
– Few data requirements
– Short-term accuracy
– Saving as necessary
The Harrod-Domar Model

Weaknesses
– Saving as sufficient

Investment is uncertain, subject to
inefficiency, etc.
– Rigid assumption of fixed proportions
No diminishing returns; no factor substitution
 No technological change
 Un-realistic lack of response of v to policy,
changes in income levels, etc.

– Development should raise ICOR endogenously
The Harrod-Domar Model

Still widely used to calculate financing
gaps
s
g  d
– How much foreign assistance to
v
achieve a particular rate of output growth?
d
v
sprivate
spublic
sforeign
g
5%
3%
10%
-3%
8%
5%
3%
10%
-3%
2%
5%
3%
10%
-3%
5%
“Technical Change and the Aggregate Production Function,”
Review of Economics and Statistics 39 (August 1957), 312-20.
Solow Growth Model


Drop fixed coefficients
Neoclassical production function
– Factor substitution, depending on factor
availability, marginal product, and prices
Y=200,000*$50=$10,000,000
K/Y=$24,000,000/$10,000,000
=2.4
$24
$20
$17
Y=200,000*$50=$10,000,000
K/Y=$20,000,000/$10,000,000
=2
Y=200,000*$50=$10,000,000
K/Y=$17,000,000/$10,000,000
=1.7
Solow Growth Model

Because factors can be substituted for
each other, policy (and the market)
can encourage the use of abundant
inputs by making scarce resources
more expensive.
Solow Growth Model
Y  F ( K , L)
Y
K
 F 
L
L
y  f (k )


Constant returns to scale
Diminishing returns to capital
Solow Growth Model
K  sY  dK


The capital stock grows as more is
saved out of output…
and declines as more capital
depreciates.
Solow Growth Model
k

K

L
k
K
L
k sY  dK

n
k
K
k sY

 n  d 
k
K
sY
k 
k  n  d k
K
sY
k 
 n  d k
L
k  sy  (n  d )k
Solow Growth Model
K
  k  sy  n  d k
L

The amount of capital per worker
– grows as more is saved out of output…
– declines as more capital depreciates…
– and declines as population grows faster
Solow Growth Model
k  sy  n  d k
Capital
deepening
Saving
-
Required
for capital
widening
Solow Growth Model
y  f (k )
sy  sf (k )
k  sy  n  d k
Steady state
change in k =
Solow Growth Model
k  sy  n  d k

In the steady state, k=0
sy*  sf k *  n  d k *

n  d k *
f k * 
s
Getting a Sense
of the Magnitudes

Assume the production function is: Y  K L
 Output per worker is:
Y
K L
K L
K



L
L
L
L L
 That is, the first relation of the model
(capital/worker determines output) is
Y
K
y k 
L
L
Getting a Sense
of the Magnitudes
 And the second relation of the
model (output determines capital
accumulation) is
k  sy  d  nk
 Then,
k  s k  d  n k
Getting a Sense
of the Magnitudes
k  s k  d  n k

In steady state,


s
k

d

n
k
the left side equals zero:
 Squaring both sides,
s k   d  nk 
2
 Dividing by k and rearranging,
2
 s 

 k*
d n
2
Getting a Sense
of the Magnitudes
2
 s 

 k*
d n
 The steady state capital per worker is equal to the
square of the ratio of the saving rate to the
depreciation rate + population growth rate.
 Steady-State Output per worker is given by:
2
s
 s 
y*  k *  
 
d n
d n
Getting a Sense
of the Magnitudes
s
y* 
d n


Steady-state output per worker is equal to the
ratio of the saving rate to the depreciation
rate+population growth rate.
A higher saving rate, a lower depreciation rate,
and a lower population growth rate lead to
higher steady-state capital per worker and
higher steady-state output per worker.
Solow Growth Model

At the steady state
–y
–k
–Y
–K
stays constant
stays constant
grows at the rate n
grows at the rate n
Solow Growth Model
1.
2.
3.
Ceteris paribus, poor countries have
much larger growth potential.
Ceteris paribus, growth will slow as a
country gets richer
Ceteris paribus, poor and rich
countries will converge.
Solow Growth Model
output / worker, y
Depreciation / worker, dk*
Output / worker, f(k*)
Saving / worker, sf(k*)
kpoor
krich Steady State capital / worker, k*
Effects of Changes in the
Saving Rate



Higher saving rate leads to more
investment…
Capital accumulates faster…
But eventually diminishing returns
lead to an end to growth.
(at a higher steady state level of output)
Effects of Changes in the
Population Growth Rate


Higher population growth rate requires
more capital for widening… for a given
sy,
So k and y decline to a lower steady
state
Y*
s
 y* 
L
d n

But because L is growing faster, Y*
must grow faster to keep y* constant.
Same, different

Different steady states will result from
– Different production functions.
Before we found that if
Y K L
then
2
 s 
and y*  s
k*  

d n
d n
Likewise, if Y  K 
1/ 3
then
 s 
k*  

d n
3/ 2
L 2 / 3
and y*  
1/ 2
s 

d n
Same, different

Different steady states will result from
– Different levels of saving, depreciation,
and population growth
s
y* 
d n
Same, different

Two countries may have the same
level of output, but different growth
rates if they have different steady
states
k  s1 y  n1  d1 k
k  s2 y  n2  d2 k
Technological change
Y  F K , T  L




Technology “T” augments labor.
Technological improvements increases
output
… without adding workers.
Requirements for capital widening
don’t increase.
Technological change allows output
per worker to increase.
Technological change
Y  F K , T  L



Assume technology grows at a
constant rate, q.
If q = 1 and n = 2,
Population growth is 2% but “effective
population growth” is 3%.
keffective  syeffective  n  d  q keffective
Dynamics of Capital and
Output
Rate of growth of:
Capital per effective worker
0
Output per effective worker
0
Capital per worker
q
q
n
Output per worker
Labor
Capital
Output
q+n
q+n
The Solow Growth Model

Strengths
– More flexibility
– Emphasizes role of saving and
technological change
– Emphasizes transition between current
output and steady-state output
The Solow Growth Model

Weaknesses: does not explain source
of
– Technological growth
– The shape of the production function
– Saving rate; population growth rate;
depreciation rate
The Solow Growth Model

Productivity is key and related to
– economic and political stability;
– health and education;
– governance and institutions;
– trade and openness;
– geography.
Two-Sector Models
Two-Sector Models

Captures key element of development:
rise in share of industry.
Two-Sector Models



Diminishing returns to labor (keeping
land fixed)
Labor surplus: marginal worker has
marginal product = 0
Agricultural wage = Average Product
– Hence Wage > MPL
Wage: Industry
must pay at
least this to farm
workers to get
them to switch
As people leave agriculture, farm output doesn’t fall for a while,
but later it starts to fall …
Direction of increase in
labor input in industry
As people leave agriculture, farm marginal product doesn’t change
for a while, but later it starts to rise …
Direction of increase in
labor input in agriculture
Direction of increase in
labor input in industry
As people leave agriculture and join industry, farm marginal product doesn’t change
for a while, keeping farm and industry wages constant. Later, as farm output falls
more and farm MP rises, wages begin to rise for farmers and for industry workers.
Two-Sector Model



Capital-owners reinvest their profits and
accumulate capital
Capital accumulation in industry allows for
more employment (higher MPL in industry).
More labor can be hired at a constant wage
because there’s surplus labor in the rural
sector.
– This keeps industrial profits going

As capital accumulates, labor shifts from
agriculture to industry.
Two-Sector Model

Eventually, there’s no surplus labor,
labor supply becomes upward sloping
– Wages begin to rise
– Food prices begin to rise
– The economy has developed
Two-Sector Model and
Population Growth

As population grows,
– More workers are added to the labor
surplus
– Same food is divided among more people
– Industrial wages fall
– In this model, population growth is
undoubtedly bad.
Neo-Classical
Two-Sector Model

Suppose there is no surplus labor
– Then any transfer of labor to industry
raises wages.
– Agricultural productivity must grow fast
so that higher wages don’t translate into
higher prices, chocking off industrial
profits and growth.
– Population growth raises farm output
(there’s no point of MPL=0), so it may be
good.
Endogenous Growth
Models
New Growth Theory:
Endogenous Growth

Motivation for the new growth theory
– Neoclassical theory predicts extremely
high rates of return in low-capital
countries. But it’s not so.
– Maybe growth “generates itself”, i.e., it is
endogenous:

poor countries generate little growth, not
because of outside forces but because of
internal (dis)incentives.
New Growth Theory:
Endogenous Growth

New growth theory
– Discards diminishing returns:
– Accumulation of HUMAN capital offsets diminishing
returns to capital.

Human capital accumulation responds to incentives.
– There can be increasing returns due to externalities.

One person’s knowledge spills over to another person, leading
to increasing returns. This may reduce incentives to acquire
skills.
– Technology is no longer essential in explaining the
Solow Residual.
New Growth Theory:
Endogenous Growth

New growth theory
– Education and physical capital are
complementary: No diminishing returns.
– There’s sustained long-term growth;
– Education and Capital accumulation are
important;
– There’s no convergence;

Lack of complementary inputs (education,
infrastructure, R&D) leads to low rates of return to
capital and therefore low capital accumulation.
New Growth Theory:
Endogenous Growth

New growth theory
– Externalities imply that the private returns to
education are much lower than the social
returns.
– Governments can generate growth by
investing in infrastructure or by funding
knowledge-intensive industries.
– The key is to generate spillovers that will make
production more profitable.
New Growth Theory:
Endogenous Growth


For rich countries, growth may be selfgenerating because of externalities in the
industry of Research and Development
(New Growth Theory applies).
But poor countries can grow without big
R&D departments, rather by appropriating
technology from rich countries (Solow
Model applies).
Coordination Failures
Underdevelopment as a
Coordination Failure



Coordination failures occur when agents’
inability to coordinate their actions leads to
an outcome (an equilibrium) that makes all
agents worse off compared to another
equilibrium.
In development, many factors must be
present and effective at the same time, so
there’s need for coordination.
Complementarities depend on networks,
where results depend on other people’s
actions.
Underdevelopment as a
Coordination Failure


Government has a role in coordinating
the acquisition of skills and investment in
production processes that will use those
skills.
Government can both help and hinder
development, because a one-time choice
can put the economy in either the good
or the bad equilibrium.
Underdevelopment as a
Coordination Failure


Suppose farmers are trying to choose what to
produce.
If they choose one product, a middleman will
arise.
– Middlemen are necessary because they acquire
information and they guarantee the quality of the
product.
– A quality guarantee allows for sales to the city.


But if everyone produces something different,
no middleman arises and production is low.
Communication, continued leadership, and
knowledge of key agents are essential.
Multiple Equilibria: A
Diagrammatic Approach




Generally, these models can be diagrammed by
graphing an S-shaped function and the 45º line.
The privately rational decision is on the vertical axis;
the expected decision by other agents is on the
vertical axis.
In this type of situation, private actions by one agent
only make sense if other agents undertake the
appropriate complementary action.
Then an equilibrium is found when the privately
rational decision is matched by the expected decision
by others.
Multiple Equilibria: A
Diagrammatic Approach


For example, an equilibrium is found when
the privately rational level of investment is
matched by the expected level of
investment by others.
Suppose a country is considering building a
factory to produce keyboards with better
design.
– The level of investment is to be decided. This
will determine the capacity of the factories: to
produce 100 or 1,000,000 keyboards per year.
Multiple Equilibria: A
Diagrammatic Approach



Building new-keyboard factories makes
sense only if, at the same time, other
countries build computer-making factories
that will use those keyboards.
Other countries are considering building the
necessary computer-factories, but only if the
keyboards are available.
So these actions are complementary, not
competitive.
Multiple Equilibria: A
Diagrammatic Approach



If country B expands the capacity of its computer
factory, country A adjusts its expectations and
expands the capacity of its keyboard factory.
As country A enlarges the keyboard factory, this
action feeds back into computer-builders, who build
larger computer factories.
So more keyboards lead to more computers which
lead to more keyboards and to more computers and
to more…
– Some capacity may be installed even without any action
by others.

The “S” has a positive intercept.
Multiple Equilibria: A
Diagrammatic Approach





If expected C capacity is more than K capacity, K
capacity increases.
If K capacity is more than expected C capacity, K
capacity falls.
Equilibrium is found where the capacity of
keyboard-factories matches the expected capacity
of computer-factories.
Does this process converge (i.e., come to a sensible
stop) or does it diverge (keep going forever)?
Are there multiple equilibria?
Stable, Unique
Equilibrium
Private action
45°
The slope of this line is
determined by the
“feedback” effect of
others’ expected actions on
private decisions.
E
Here $1 of others’ investment
creates less than $1 of private
investment.
To the left of E, private
investment increases, which
changes others’ expectations
and actions. This is fed back
because others’ actions affect
private expectations.
Feedback slows down as E is
approached.
Past E, private investment falls
towards E.
Expected action
by others
Unstable, Unique
Equilibrium
Private action
Here $1 of others’
investment creates
more than $1 of
private investment:
there’s increasing
E
feedback.
45°
Below E, private investment
decreases.
This causes others to reduce
their investment by $X,
which reduces private
investment by more than
$X.
Negative feedback speeds
up as the economy moves
away from E.
Past E, private investment
rises, faster and faster.
Expected action
by others
Multiple Equilibria
Equilibria are stable
when the function
crosses the 45º line
from above; and
unstable when the
function crosses the
45º line from below
Kremer’s O-Ring Theory of
Economic Development

The O-ring model
– Modern production requires many
activities done well together in order for
any of them to amount to high value.
– Suppose that in a production process
there are n activities.
– They can be carried out in a variety of
ways, each of which gives a quality q to
the outcome. Order the methods by q.
Kremer’s O-Ring Theory of
Economic Development

The O-ring model
– Suppose there are different types of workers, each with skills
so that they can produce a quality q.
– The model shows that…


If workers are imperfect substitutes for one another (which is
true)…
And if workers’ tasks are complementary (which is often true)…
– Then high-quality workers will match with other high-quality
workers; low-quality workers will also get together. The
reason is that production (and therefore wages) are higher if
there is this “matching” than if there isn’t.
– Then some firms (or countries) may be caught in low-quality
(i.e., under-development) traps
The O-Ring Production
Function: Wage as a Function
of Human Capital Quality
As average
skill increases,
wages go up
faster than
proportionately
to one person’s
skill – because
my
productivity
depends on
other people’s
skills.
Therefore my incentive
to acquire skills
depends on whether
other people acquire
skills at the same time.
There are “o-rings”:
low-quality parts that
can cause a collapse of
the whole. Therefore
public qualityenhancing programs
may be needed.
Kremer’s O-Ring Theory of
Economic Development

Implications of the O-ring theory
– Bottlenecks can arise, making the whole collapse.


Absolute bottlenecks rarely exist because people can work
around low-quality co-workers or industries.
One important work-around is international trade: openness
leads to growth.
– Complicated technologies require high-skill workers.


Therefore only firms (and countries) that can afford to get
high skill workers will adopt high-value, complicated
technologies.
Brain drain follows: why people get paid more, for the
same skills, when they move.
Coordination Failure


It’s clear that problems are very deep, and that a series
of small failures can lead to huge traps.
Some coordination problems can be solved by a onetime fix.
– This is an attractive area for public policy because the costs may
be small but the benefits, forever, may be large.

These models also imply that the destructive potential of
government is enormous.
– It can lead the economy from a better equilibrium to a worse
one.
– Similarly for international aid.