* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Category 2 Geometry Meet #3 – Study Guide
Euler angles wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
History of geometry wikipedia , lookup
Four color theorem wikipedia , lookup
Perceived visual angle wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
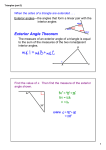
Category 2 Geometry Meet #3 – Study Guide Topics : Properties of polygons & Pythagorean Theorem Diagonals of a polygon : When finding the number of diagonals in a polygon, first consider the number of diagonals that come from each vertex. You can not connect a vertex to itself or to the vertex directly to the right or left. In the diagram below you can see that a randomly chosen vertex has 3 diagonals that originate from that vertex. Since there are 6 vertices, each vertex will have 3 diagonals coming out of it. So that would make 3 x 6 = 18 diagonals. However if we figure it out that way we will have counted each diagonal twice, so we must now divide by 2. So there are 18 ÷ 2 = 9 diagonals. Interior and exterior angles : When trying to find the number of degrees in either the interior or exterior angle of a regular polygon you have two methods to choose from. To get the interior angle right off, you can find the total number of degrees in the polygon and then divide by the number of sides. You can find the total number of degrees by drawing a picture like the one above and to the right. The hexagon can be divided into 4 triangles each with 180 total degrees in the sum of their angles. That's a total of 4 x 180 = 720 degrees. Each interior angle would then have 720 ÷ 6 = 120 degrees. Since the exterior angle needs to be supplementary to the interior angle, the exterior angle = 180 – 120 = 60 degrees. **An easier method would be to note that the sum of the exterior angles of any polygon is equal to 360 degrees(as long as you take only one of the exterior angles per vertex and they all go either clockwise or counter clockwise. See the picture below to see a+b+c+d+e+f = 360). So if the exterior angles add up to 360 and there are 6 exterior angles, they would each be 360 ÷ 6 = 60 degrees. Since the exterior angle needs to be supplementary to the interior angle, the interior angle = 180 – 60 = 120 degrees. a b f c e d Category 2 Geometry Meet #3– Study Guide – continued Pythagorean Theorem : Stated properly : " The sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse". Stated more plainly : In a right triangle if you square the sides that make the right angle and add them together you will get the same as if you squared the longest side opposite the right angle. Also you can think about it as an area problem. The sum of the areas of the two smaller squares is equal to the area of the larger square.(It is interesting to note that if instead of squares you make triangles that are all similar, or semi-circles, or regular polygons the same area relationship would be true.) The classic statement of the Pythagorean Theorem and proper use in the problem below would be a2 + b2 = c2 c a b It will be very beneficial if you commit to memory the squares of the numbers as high as you can to speed up Pythagorean Theorem problems. Another great thing to memorize are the Pythagorean Triples. This is where the sides of a right triangle are all whole numbers. The common Pythagorean Triples are 3-4-5, 5-12-13, 7-24-25, 8-15-17, 9-40-41 you can also multiply all three numbers by the same thing. For example 3-4-5 multiplied by 3 = 9-12-15 and 92 + 122 = 152. Here are the squares of the first 30 whole numbers to study : 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900