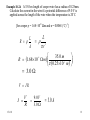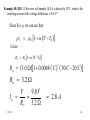Download resistance

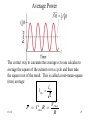
Chapter 18
© 2006, B.J. Lieb
Some figures electronically reproduced by
permission of Pearson Education, Inc., Upper
Saddle River, New Jersey Giancoli, PHYSICS,6/E
© 2004.
Ch 18
1
Simple Electric Cell
Carbon
Electrode
(+)
+
+
+
_
_
_
Zn
Electrode
(-)
Zn+ Zn+
Zn+ Zn+
Sulfuric acid
•Two dissimilar metals or carbon rods in acid
•Zn+ ions enter acid leaving terminal negative
•Electrons leave carbon making it positive
•Terminals connected to external circuit
•‘Battery’ referred to several cells originally
Ch 18
2
Electric Current
•If we connect a wire between the two terminals
electrons will flow out of the negative terminal and
toward the positive terminal we have an electric
current.
•Electric current I is defined as the net amount of charge
that flows past a given point per unit time.
Q
I 
t
1 C/s = 1A (ampere)
An ampere is a large current and often currents
are mA (10-3 A) or A (10-6 A).
Ch 18
3
Electric Circuit
• It is necessary to have a complete circuit in order for
current to flow.
• The symbol for a battery in a circuit diagram is:
+
_
Device
+
Ch 18
4
“Conventional” current direction is opposite to actual
electron flow direction which is – to +.
Ch 18
5
Ohm’ Law
• For wires and other circuit devices, the current is
proportional to the voltage applied to its ends:
IV
• The current also depends on the amount of resistance that
the wire offers to the electrons for a given voltage V. We
define a quantity called resistance R such that
V = I R (Ohm’s Law)
• The unit of resistance is the ohm which is represented by
the Greek capital omega ().
• Thus
V
1 
Ch 18
A
6
Resistors
• A resistor is a circuit device that has a fixed resistance.
Resistor
Circuit symbol
Resistors obey Ohm’s law but not all circuit devices do.
I
I
0
V
Resistor
Ch 18
0
V
non-ohmic device
7
Example 18-1A. A person experiences a mild shock if a current of 80 A flows
along a path between the thumb and the index finger. The resistance of this path is
4.0x105  when the skin is dry and 2000  when the skin is wet. Calculate the
minimum voltage difference between these two points that will produce a mild shock.
V  IR
V
DRY

80 10
6
A4.0 10  
5
 32 V
V
W ET

80 10
6
A2.0 10  
3
 0.16 V
Ch 18
8
Example 18-1B. Calculate the number of electrons per second that
flow past a point on the skin in problem 18-1A.
Q
I 
t
# electrons
 Q 


sec
 t 
 charge 


 electron 
 Q   1 electron 
 




 t   1.6 10 C 
19

 80 10
6
C

 1 electron 


s  1.6 1019 C 


electrons
 5.0 10
sec
14
Ch 18
9
Resistivity
• In most electronic circuits we ignore the resistance of the
wires because it is small in comparison to the other circuit
components
• If we need to calculate the resistance of a given wire we can
use its resistivity () which is defined by:
L
R  
A
where L is the length of the wire and A is the cross
sectional area.
A
L
Ch 18
10
Resistivity and Temperature
Ch 18
11
Resistivity and Temperature
•Resistivity usually depends on temperature. For most metals
the resistivity increases with temperature.
•Often the flow of current through a wire is the cause of the
temperature change.
T  0 1   (T  T0 )
where T0 is usually 20o and 0 is the resistivity at that
temperature.
Ch 18
12
Example 18-2A A 35.0-m length of cooper wire has a radius of 0.25mm.
Calculate the current in the wire if a potential difference of 9.0 V is
applied across the length if the wire when the temperature is 20˚C.
[for cooper ρ = 1.68×10-8 Ωm and α = 0.0068 (˚C)-1]
L
R  
A
L
 
r
2


35.0 m
R  1.6810  m 

  0.2510 m  
8
3
2
 3.0 
V  IR
V
I 
R
Ch 18

9.0 V
3.0 
 3.0 A
13
Example 18-2(B) If the wire in Example 18-2A is heated to 30˚C, what is the
resulting current if the voltage difference is 9.0 V?
Since R α ρ, we can see that:
T   0 1  T  T0 
Gives:
RT  R0 1  T  T0 
R
30
R
30
I
 3.0  1 0.0068  C 

30
1
 30 C  20 C 


 3.2 
V
9 .0 V


R
3.2 
 2.8 A
30
Ch 18
14
Superconductivity
•The resistivity of certain metals and
compounds becomes zero at low
temperatures near absolute zero- this
state is called superconducting.
•Occurs only below a critical
temperature TC which is usually close
to absolute zero
• Materials require liquid helium for cooling.
• Since 1987 a new class of “high TC” materials have been
discovered that are superconducting up to 160 K.
• Would be many practical applications if some of the
difficulties can be overcome.
Ch 18
15
Power in Electric Circuits
• Electrical circuits can transmit and consume energy.
• When a charge Q moves through a potential difference V,
the energy transferred is QV.
• Power is energy/time and thus:
energy
QV
Q   IV

P  power 

  V
time
t
 t 
and thus:
P  IV
Ch 18
16
Notes on Power
•The formula for power applies to devices that provide
power such as a battery as well as to devices that consume
or dissipate power such as resistors, light bulbs and electric
motors.
J
C  J 
P  IV      
 W  watt
s
 s C 
•For ohmic devices, the formula for power can be combined
with Ohm’s Law to give other versions:
P  IV  I ( I R)  I2 R
Ch 18
V2
V 
P  IV    V 
R
 R
17
Household Power
•Electric companies usually bill by the kilowatt-hour
(kWh.) which is the energy consumed by using 1.0 kW for
one hour.
•Thus a 100 W light bulb could burn for 10 hours and
consume 1.0 kWh.
•Electric circuits in a building are protected by a fuse or
circuit breaker which shuts down the electricity in the
circuit if the current exceeds a certain value. This prevents
the wires from heating up when carrying too much current.
Ch 18
18
Connection of
Household
Appliances
Ch 18
19
Example 18-3 (A) A person turns on a 1500 W electric heater, a 100 W hair
dryer and then a 300 W stereo. All of these devices are connected to a single
120 V household circuit that is connected to a 20 A circuit breaker. At what
point will the circuit breaker trip off?
P  IV
P
I 
V
I
I
I
I
heater
bulb
dryer
stereo
Ch 18
1500 W

 12.5 A
120 V
100 W

 0.83 A
120 V
1000 W

 8.3 A
120 V
300 W

 2.5 A
120 V
 Circuit breaker
trips with dryer
20
Example 18-3 (B) If electricity costs $0.12 per kWh., calculate the cost of
operating all the appliances in the above problem for 2.0 hours.
Heater cos t  1.5 kW 2 h $ 0.12 kWh
 $ 0.36
Bulb
 $ 0.024
Dryer  $ 0.24
Stereo  $ 0.072
$ 0.70
Ch 18
21
Alternating Current
•Electrical power is
distributed using
alternating current (ac)
in which the current
reverses direction with a
frequency of 60 Hz (in
the USA).
Ch 18
22
Alternating Current
The current and voltage varies as a sine function as
shown above. Thus
V  V0 sin 2 ft
Ch 18
23
Average Power
•Even though the electron motion in ac circuits is back and
forth they can still deliver power.
•Because the current and voltage change greatly over a cycle,
we have to average over a cycle to get an accurate value for
the average power consumed in the circuit
Ch 18
24
Average Power
The correct way to calculate this average is to use calculus to
average the square of the current over a cycle and then take
the square root of the result. This is called a root-mean-square
(rms) average:
I0
I rms 
2
Ch 18
2
V
2
P  I rms
R  rms
R
25
Alternating Current/Voltage in U.S.
I  I 0 sin 2 ft
V  V0 sin 2 ft
•In the U.S.: f = 60 Hz
V0  170 V
Vrms 120 V
Ch 18
•In Europe: f = 50 Hz
V0  310 V
Vrms  220 V
26
Example 18-4 (A) A heater coil connected to a 240-V ac line has a resistance
of 34 Ω. What is the average power used?
P  I
P 
2
rms
V

R
V
rms
rms
240V 2
 1.7 kW
34 
(B) What are the maximum and minimum values of the instantaneous power?
I
I
rms
0
V
0

I

2
2I

rms
2V
rms
P  I V
0
0
0
0

2I
rms
rms
 (2) P
 (2) I V
 3.4 kW
rms
Ch 18
2 V
rms
 (2) (1.7 kW )
27
Microscopic View of Current
•Read Example 18-14. It studies a 5.0A current in a copper wire that is
3.2 mm in diameter. It finds that the average “free” electron moves with
a velocity of 4.7 x 10-5 m/s in the direction of the current. This is called
the drift velocity.
•It also assumes the “free” electrons behave like an ideal gas and
calculates that the thermal velocity of the average electron is 1.2 x 105
m/s.
•Thus in a wire carrying a current, the electron motion is largely random
with a slight tendency to move in the direction of the current. Thus if
you could see electrons in a wire carrying current they would appear to
be moving randomly.
Ch 18
28
Summary of Units
Ch 18
29