Download Chapter 29 Alternating Currents and Power Transmission

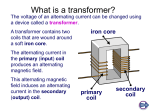
Electricity and Magnetism
Chapter 29
Alternating Currents and
Power Transmission
29
Alternating Currents and Power Transmission
Electricity and Magnetism
29.1 Alternating current
Alternating currents and alternating voltages
• In a direct current (d.c.) circuit, electric current flows in one
direction only.
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• In an alternating current (a.c.) circuit, current reverses its
direction periodically.
• In general, a.c. are produced by alternating e.m.f.s (voltages)
from a.c. sources.
Square waveform
29
Sinusoidal waveform
Alternating Currents and Power Transmission
Electricity and Magnetism
• A sinusoidal alternating voltage can be expressed as
V = V0 sin wt
where V0 is its peak value and w is its angular frequency.
• The angular frequency w is
related to the frequency f
and the period T of the
voltage by
2π
w  2 πf 
T
29
Alternating Currents and Power Transmission
V0
T
2π
w
−V0
Electricity and Magnetism
Resistive circuit
• In a purely resistive circuit,
V and I are in phase.
V = V0 sin wt
Example 29.1
29
I = I0 sin wt
Checkpoint (p.418) O
Alternating Currents and Power Transmission
Electricity and Magnetism
Root-mean-square (r.m.s.) values
• Applying P = VI, for sinusoidal
voltage and current, the
instantaneous power supplied to
the load is
P = V0I0 sin2wt
• However, what we really concern is the average power of an
a.c. supplied to a resistive load, which is given by
P  I R  I R
2
where the symbol
enclosed quantity.
29
2
denotes the time-average of the
Alternating Currents and Power Transmission
Experiment 29.1
Electricity and Magnetism
I 2  I 0 sin wt
2
• For a sinusoidal voltage, we have
1 2
2
I  I0
2
• The root-mean-square (r.m.s.)
value of a current I is defined as
I rms 
I2
• Hence, for sinusoidal voltages, we have I rms
• Since
P  I 2 R , we have
I0
.

2
P  I rms R
2
R.m.s. values of alternating currents of square waveform
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• In other words,
The root-mean-square (r.m.s.) value of an a.c. is the
steady d.c. which delivers the same average power
as the a.c. to a resistive load.
• The average power can be expressed in the following forms:
Vrms
2
P  Vrms I rms
P 
P  I rms R
R
• For sinusoidal alternating currents and voltages, we have
I0
V0
Vrms 
I rms 
2
2
Example 29.2
29
Checkpoint (p.423) O
Alternating Currents and Power Transmission
Electricity and Magnetism
29.2 Transformer
• A transformer is a device that can change the value of an
alternating voltage.
A transformer for
notebook computers
29
Substations contain a lot of
transformers.
Alternating Currents and Power Transmission
Electricity and Magnetism
Structure and working principle of a simple
transformer
• A change in current through a coil induces a voltage in
another nearby coil due to the change in magnetic field
through the latter coil.
• This effect is called mutual induction.
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• The primary coil of a transformer is connected to an a.c.
source and the secondary coil gives the output voltage.
• If the magnetic flux through each turn of the coils in a
transformer is the same, there is perfect flux linkage (i.e. no
flux leakage) between the coils.
29
Alternating Currents and Power Transmission
Electricity and Magnetism
Voltages and currents in transformers
• The voltage ratio and turns ratio of a transformer, with perfect
flux linkage and negligible coil resistance, are related by
Vs N s

Vp N p
Experiment 29.2
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• Apply Faraday’s law, the alternating magnetic flux through
the coils induce e.m.f.s in the coils.
 p
s
 p  Np
 s   Ns
t
t
• With the iron core, the magnetic flux through each turn of the
two coils is the same.
 s Ns
 p  s

 p   s

 p Np
t
t
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• For a step-up transformer, Ns > Np, and so Vs > Vp.
• For a step-down transformer, Ns < Np, and so Vs < Vp.
• The efficiency of a transformer can be expressed as
I sVs
output power
efficiency 
100 % 
100 %
input power
I pVp
Transformer
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• An ideal transformer has 100% efficiency. For such a
transformer, we have
Ip
Vs

I s Vp
Vs N s
• Since
, we have

Vp N p
Ip
Ns

Is N p
• Hence, for an ideal transformer, whenever the voltage is
stepped up (or stepped down), the current through the
secondary coil decreases (or increases) by the same factor.
Example 29.3
29
Example 29.4
Checkpoint (p.431) O
Alternating Currents and Power Transmission
Electricity and Magnetism
Energy loss in transformers and practical
transformer designs
• Transformers have very high efficiency, but are never ideal.
reasons for energy loss
improvements made in
practical transformers
resistance in the coils
use thick copper wires to
make the coils
continuous magnetization
and demagnetization of the
iron core
29
use high-quality
magnetic materials to
make the core
Alternating Currents and Power Transmission
Electricity and Magnetism
reasons for energy loss
improvements made in
practical transformers
eddy currents in the iron
core
use a laminated core
Checkpoint (p.433) O
29
Alternating Currents and Power Transmission
Electricity and Magnetism
29.3 Transmission and distribution of
electricity
Power loss in transmission lines
• One of the problems in
transmitting electricity is the
power loss in the transmission
lines due to the heating effect of
current.
Overhead transmission lines
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• If a transmission line carries a current I and has a resistance
R, the power dissipated as heat is given by
P = I2R
• The lower the current, the lower
the power dissipated.
• Using transformers, a.c. voltage
can be stepped up easily and
efficiently, and the current can be
stepped down accordingly.
• Hence, alternating current is
used to transmit mains electricity
in order to reduce the power loss.
Overhead transmission lines
Experiment 29.3
Example 29.5
29
Alternating Currents and Power Transmission
Electricity and Magnetism
Grid system in Hong Kong
• A grid system is a transmission and distribution network of
mains electricity.
29
Alternating Currents and Power Transmission
Electricity and Magnetism
• The voltage of the electricity generated at a power station is
stepped up before transmission and stepped down
successively at substations in populated areas.
Schematic diagram of the grid system in Hong Kong
Birds on transmission lines
29
Alternating Currents and Power Transmission
Checkpoint (p.441) O