Download Solutions - Georgia Tech

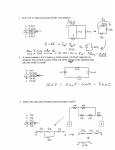
PHYS 3123
Georgia Tech, Spring 2017
Homework 2 Solutions
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
1. (Problem 7.15) A long solenoid with radius a and n turns per unit length carries a time-dependent current I(t) in
the φ̂ direction. Find the electric field (magnitude and direction) at a distance s from the axis (both inside and
outside the solenoid), in the quasistatic approximation.
Solution: In the quasistatic approximation, we can use magnetostatics to calculate the magnetic field on the
right-hand-side of Faraday’s law: ∇ × E = −∂B/∂t (using the quasistatic approximation here means that
we are assuming the current I(t) isn’t changing rapidly). Thus, the magnetic field at a distance s from the
axis is given by
µ0 nI(t)ẑ, 0 ≤ s ≤ a
B(sŝ) =
0,
s≥a
Therefore, we need to find an E to solve the equation
−µ0 nI 0 (t)ẑ, 0 ≤ s ≤ a
∇×E=
0,
s≥a
(1.1)
There are different ways to solve this. One way using the integral formulation of Maxwell’s equations is
given in the solutions manual. I will give another by solving the above PDE by inspection.
If we review the form of ∇ × E for cylinderical coordinates (i.e., looking inside of the front cover of the
4th edition), we immediately see that ∇ × E must result in only a ẑ component in order to satisfy (1.1).
Moreover, from symmetry considerations we note that E may only have a φ̂ component. Therefore, (1.1)
becomes
1 ∂
−µ0 nI 0 (t)ẑ, 0 ≤ s ≤ a
∇×E=
(sEφ )ẑ =
0,
s≥a
s ∂s
We immediately see that Eφ (s, t) = − 12 µ0 nI 0 (t)s for 0 ≤ s ≤ a. For outside the loop s ≥ a, we must solve
Eφ + s
dEφ
C
= 0 −→ Eφ (s, t) =
ds
s
The boundary condition is given by s = a, which tells us that C = − 12 µ0 nI 0 (t)a2 . Putting everything
together, we conclude
µ0 nI 0 (t)s
φ̂,
2
µ0 nI 0 (t)a2
E(s, t) = −
φ̂,
2s
E(s, t) = −
0≤s≤a
s≥a
2. (Problem 7.18) A square loop, side a, resistance R, lies a distance s from an infinite straight wire that carries a
current I (Fig. 7.29, 4th edition). Now someone cuts the wire, so I drops to zero. In what direction does the
induced current in the square loop flow, and what total charge passes a given point in the loop during the time this
current flows? If you don’t like the scissors model, turn down the current gradually:
(1 − αt)I, for 0 ≤ t ≤ 1/α
I(t) =
0,
for t > 1/α
PHYS 3123
Georgia Tech, Spring 2017
Homework 2 Solutions
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
Solution: This problem is similar to problem 7.8 from HW 1, so we use quote results from that solution
here. The magnetic flux through the loop due to the long straight wire will be
Φ(t) =
µ0 I(t)a a
ln 1 +
2π
s
Since the current is decreasing, Lenz’s law tells us that nature will try to maintain the original flux and,
therefore, a counterclockwise current will appearing in the loop. To find the total charge passing through any
given point in the loop we compute
E = Iloop R =
dQloop
µ0 a a dI
R=−
ln 1 +
dt
2π
s dt
Thus,
Q=
µ0 aI a
ln 1 +
2πR
s
The minus sign disappeared because dI/dt < 0.
3. (Problem 7.20) Where is ∂B/∂t nonzero, in Fig. 7.21(b) (4th edition)? Exploit the analogy between Faraday’s
law and Ampere’s law to sketch (qualitatively) the electric field.
Solution: ∂B/∂t is nonzero on the boundary of the square region encompassing B (this is where B is
changing instantaneously in time). The corresponding electric field circulates counterclockwise (the same
direction as I in the diagram).
4. (Problem 7.24) Find the self-inductance per unit length of a long solenoid, of radius R, carrying n turns per unit
length.
Solution: The magnetic field inside the solenoid is B = µ0 nI and so the magnetic flux through a single
turn is Φsingle turn = πR2 µ0 nI. There are nl turns through a length l, so the magnetic flux through nl turns is
Φ = πR2 µ0 n2 Il. Since the self-inductance L is defined as the proportionality constant between Φ and I, we
find that the self-inductance per unit length is µ0 πR2 n2 .
5. (Problem 7.28) Find the energy stored in a section of length l of a long solenoid (radius R, current I, n turns per
unit length), (a) using Eq. 7.30 (you found L in Prob. 7.24); (b) using Eq. 7.31 (we worked out A in Ex. 5.12);
(c) using Eq. 7.35; (d) using Eq. 7.34 (take as your volume the cylindrical tube from radius a < R out to radius
b > R).
Solution:
(a) Eq. 7.30 reads W = LI 2 /2 and, using the previous problem, L = µ0 πR2 n2 l. Hence,
1
W = µ0 πR2 n2 I 2 l
2
Page 2
PHYS 3123
Georgia Tech, Spring 2017
Homework 2 Solutions
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
H
(b) Eq. 7.31 reads W1 = 2−1 (A · I)dl (this is the energy store in a single turn of the loop) and Ex 5.12
yields A = 12 µ0 nIRφ̂ on the solenoid. Hence, the energy stored in a section of length l is
I
l
1
nl
(A · I)dl = µ0 n2 I 2 R(2πR) = πµ0 n2 I 2 R2 l
W =
2
4
2
R
(c) Eq. 7.35 reads W = 2µ1 0 all space B 2 dτ . We compute this integral over the cylindrical volume of length
l and radius R (because B = 0 outside the solenoid). Since B = µ0 nI is constant, we find
1
1
(µ0 nI)2 (πR2 l) = µ0 πR2 n2 I 2 l
2µ0
2
W =
R
H
(d) Eq. 7.34 reads W = 2µ1 0 V B 2 dτ − S (A × B) · da . We take as our volume V the cylindrical tube
from radius a < R out to radius b > R, and note that A × B = 12 µ20 n2 I 2 sŝ when s ≤ R. Since B = 0
outside the solenoid,
Z
B 2 dτ = (µ0 nI)2 π(R2 − a2 )l
V
The surface S will be the surface defined the cylindrical volume V and we note that (A × B) · da
is only nonzero when we are one the inner surface defined by R = a (the two ”caps” to the cylinder
have zero contribution because da ⊥ ŝ and on the surface defined by R = b, B = 0). Noting that
da = adφdz(−ŝ) on the inner surface R = a, we have
I
1
(A × B) · da = (µ0 nI)2 a
2
S
Z
2π
Z
0
0
l
1
ŝ · adφdz(−ŝ) = − (µ0 nI)2 2πa2 l
2
Putting everything together, we find
1
1
1
2
2
2
2
2
W =
(µ0 nI) π(R − a )l + (µ0 nI) 2πa l = µ0 πa2 n2 I 2 l
2µ0
2
2
6. (Problem 7.31) Suppose the circuit in Fig. 7.41 (4th edition) has been connected for a long time when suddenly,
at time t = 0, switch S is thrown from A to B, bypassing the battery.
(a) What is the current at any subsequent time t?
(b) What is the total energy delivered to the resistor?
(c) Show that this is equal to the energy originally stored in the inductor.
Solution:
(a) Since the circuit has been connected for a long time, the current at t = 0 is given by I0 = E0 /R. Once
the switch has been flipped, the current will obey the following differential equation.
−L
dI
E0
= IR −→ I(t) = e−(R/L)t
dt
R
Page 3
PHYS 3123
Georgia Tech, Spring 2017
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
Homework 2 Solutions
(b) The power delivered to the resistor is P(t) = I 2 R and, using the same logic as we did in the problem
7.7 of the previous HW, the total energy delivered to the resistor is
Z∞
W =
E2
P(t)dt = 0
R
0
Z∞
e−2(R/L)t dt =
E02 L
2R2
0
(c) The energy originally stored in the inductor is
1
E 2L
W = LI 2 = 0 2
2
2R
which is indeed equal to what we derived in part (b).
7. (Problem 7.63) Prove Alfven’s theorem: In a perfectly conducting fluid (say, a gas of free electrons), the
magnetic flux through any closed loop moving with the fluid is constant in time. (The magnetic field lines are, as
it were, ”frozen” into the fluid.)
(a) Use Ohm’s law, in the form of Eq. 7.2, together with Faraday’s law, to prove that if σ = ∞ and J is finite,
then
∂B
= ∇ × (v × B)
∂t
(b) Let S be the surface bounded by the loop (P) at time t, and S 0 a surface bounded by the loop in its new
position (P 0 ) at time t + dt (see Fig. 7.58). The change in flux is
Z
Z
dΦ = B(t + dt) · da − B(t) · da
S0
S
Use ∇ · B = 0 to show that
Z
Z
Z
B(t + dt) · da + B(t + dt) · da = B(t + dt) · da
S0
R
S
(where R is the ”ribbon” joining P and P 0 ), and hence that
Z
Z
∂B
dΦ = dt
· da − B(t + dt) · da
∂t
R
S
(for infinitesimal dt). Use the method of Sect. 7.1.3 to rewrite the second integral as
I
dt (B × v) · dl
P
and invoke Stoke’s theorem to conclude that
Z dΦ
∂B
=
− ∇ × (v × B) · da
dt
∂t
S
Together with the result in part (a), this proves the theorem.
Page 4
PHYS 3123
Georgia Tech, Spring 2017
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
Homework 2 Solutions
Solution:
(a) Suppose J is finite and, for now, assume σ is finite, but can be made arbitrarily large. Then,
J
=E+v×B
σ→∞ σ
0 = lim
Therefore,
E = −v × B
Finally, Faraday’s law tells us that
∂B
= −∇ × E = ∇ × (v × B)
∂t
and we have the result.
H
(b) The Divergence theorem tells us that ∇ · B = 0 (this is true for all times) implies that B · da = 0
over any closed surface.H For our closed surface consisting of S, S 0 , and R, this tells us that we can
decompose the integral B(t + dt) · da over this closed surface as
I
Z
Z
Z
B(t + dt) · da = B(t + dt) · da + B(t + dt) · da − B(t + dt) · da = 0
S+S 0 +R
S0
R
S
(the sign flip in the third term comes from the change in orientation of the unit normal to the surface
from pointing outward to pointing inward). Applying this relationship to the expression of dΦ in the
problem statement, we find
Z
Z
Z
dΦ = − B(t + dt) · da + B(t + dt) · da − B(t) · da
R
Z
= dt
S
∂B
· da −
∂t
S
Z
B(t + dt) · da
R
S
Now it is crucial to note that if we are to use the first equation on page 308 (4th edition), i.e. da =
(v × dl)dt, then we must switch this equation to read da = (dl × v)dt because the orientation of the
ribbon flips when going from Fig 7.13 (4th edition) to Fig 7.58 (4th edition) (the latter being the Fig
relevant to the problem). Thus, we may write
Z
Z
B(t + dt) · da = B(t + dt) · (dl × v)dt
R
R
and the general identity for vectors a · (b × c) = c · (a × b) allows us to further write
Z
Z
B(t + dt) · da = (v × B(t + dt)) · dldt
R
R
The previous integral is already to first order in dt, so it is ”ok” to replace B(t + dt) with B(t). Doing
this and applying Stoke’s theorem leaves us with precisely
Z
I
Z
B(t + dt) · da = dt (v × B) · dl = dt ∇ × (v × B) · da
R
P
S
Page 5
PHYS 3123
Georgia Tech, Spring 2017
Homework 2 Solutions
Instructor: David Ballantyne
(Thomas) Forrest Kieffer
Plugging this back into the expression for dΦ leaves us with


Z ∂B
dΦ = 
− ∇ × (v × B) · da dt
∂t
S
Applying part (a) to this expression we find that dΦ/dt = 0 and hence the result.
Page 6