* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Single particles quantum cryptography
Survey
Document related concepts
Transcript
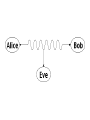
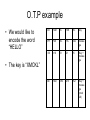
Single particles quantum cryptography. Barak Gur 2008 What is Cryptography • Cryptography is hiding information so that only the person its meant to will able to read it . • Cryptography, in its classical way, is considered as branch of both mathematics and computer science in its modern way its pure physics. • When we say Cryptography we mean encryption and decryption of information. Medieval cryptography • The very beginning of cryptography needed no more then a pen and paper, as most people could not read. • then the development of cipher text started: taking a plaintext and by using an algorithm (called cipher) we make it unreadable to anyone except those possessing the key. For example: The first and simplest cipher text Technique is rearranging the order of letters e.g. 'help me' becomes 'ehpl em'. • After that came a systematically replace of letters or groups of letters with other letters or groups of letters (e.g., 'fly at once' becomes 'gmz bu podf' by replacing each letter with the one following it in the alphabet). For example: An early substitution cipher was the Caesar cipher, in which each letter was replaced by a letter some fixed number of positions further down the alphabet. It was named after Julius Caesar who used it, with a shift of 3, to communicate with his generals. religious applications • Caesar cipher can be found in the “Mezuza”: כוזו במוכסז כוזו. • 666 or in some early manuscripts, 616, is the sum of the letters of the Roman Emperor Nero (NERO and NERON). Vulnerability of cipher text Technique • Cipher texts produced by classical ciphers always reveals some statistical information about the original text, which can often be used to break them. • An example of such use of statistical information was the discovery of frequency analysis by polymath al- Kindi at about the 9th century, nearly all such simple ciphers became more or less readily breakable by an informed attacker. • A typical distribution of letters in English language text. Weak ciphers do not sufficiently mask the distribution, and this might be exploited by a cryptanalyst to read the message. 1800 to World War 2 • In 1917 the one time pad (O.T.P) was introduced. • O.T.P is an encryption algorithm where the plaintext is combined with a random key or "pad" that is as long as the plaintext and is used only once. • If the key is truly random, never reused, and kept secret, the one-time pad provides perfect secrecy. • In fact O.T.P is the goal of Single particles quantum cryptography which will be discussed later. O.T.P example • We would like to encode the word “HELLO” 23X 12M 2C 10K 11L key +7H +4E 11L 11L 14O messa ge = 30 =16 13 21 25 Key + messa ge =4E 16Q 13N 21V 25Z Key + messa ge (mod 26) • The key is “XMCKL” World War 2 • The Enigma which is most known for being used by the Nazi’s during World War II. • Enigma was a family of related electromechanical rotor machines. • For a message to be correctly encrypted and decrypted, both sender and receiver had to set up their Enigma in the same way. • Mathematician Marian Rejewski, at Poland's Cipher Bureau, in December 1932 reconstructed the German Army Enigma, using mathematics and limited documentation. Modern cryptography • Symmetric-key cryptography: encryption in which both the sender and receiver share the same key (the only kind of encryption publicly known until June 1976). • Public-key cryptography: two different but mathematically related keys are used — a public key and a private key. • In public-key cryptography, the public key is broadcasted freely (used for encryption), while the private key remains secret (used for decryption). • The RSA encryption scheme used for internet security is based on the fact that the time taken to find the prime factors of a large number increases exponentially with the number of digits. Summary Principles of quantum cryptography • We would like to encrypt our message with a private key which will be used once (O.T.P) instead of a public one. • Quantum cryptography's purpose is to provide a secure way for exchanging this key. • The two basic schemes are of single particle and entangle states, we shell discuss the first one which is the most commonly implemented in the field. Quantum no cloning A U e A e B B A e A B U B e B AU U † A e B B A e A B A A B B 2 BB84 protocol • The protocols can use any two pairs of orthogonal polarization, we shell use the following: • Our setup is as followed: • Bob does not know which base Alice has chosen for the photon he will receive, therefore he chooses his base randomly. • In the cases he chose the same like Alice he measured the correct answer. • Alice also chooses her base randomly then they will have there basses matching for 50% of the cases. • For the other 50% Bob is using the wrong base and will get random results . The way Alice and Bob work 1. 2. 3. 4. 5. 6. 7. Alice transmits her data while choosing her basses randomly (she isn't telling which base she chose). Bob records the results he is receiving, he is choosing his base randomly. On a p.l (public line) Bob tells Alice of his Choice of basses. Alice compares it to her choice of basses and by p.l tells Bob what measurements they will eliminate. Over a p.l Bob sends Alice a subset of his results. If Alice finds that the error rate is less then 25% they conclude that the communication was secured. The remaining bits are their private key. An example of how Alice and Bob work Why 25% error indicates the presence of Eve? • • • Lets say Eve is detecting the photons Alice has sent to Bob and then transmitting a “copy” of then to Bob. Eve is choosing her base randomly, this is the best option for her. (50% of the cases she had the correct base and therefore transmitted the correct answer to Bob.) We are interested at cases in which Bob used the correct base (like Alice) at 50% of this cases Eve had the wrong base, so she transmitted using this base. Out of this cases Bob recorded the wrong answer at 50% of the cases (he has a 50%-50% chance to record a correct/wrong answer when he is using a different base then Eve). System errors • Even when Eve isn't present our system has errors, in order to be able to detect Eve present it is crucial to deal with this errors. • First error type: Random deleting of photons (caused by absorption/scattering or detector inefficiency), the way to coupe with is by Bob telling Alice Which base he chose and when did he register his result, therefore random deleting effects the efficiency of the system but not the security. • Second error type: if the medium in which the photons travel is birefringence then the polarization angle of a photon will change. The way to calibrate this error out of the system is the same like in classical data transmission (by using “Shannon's noisy channel coding theorem”) we need to make sure that the error probability is much smaller then error rate introduced by Eve. The number of bites that must be compared to correct this error is: • • Third error type: detector dark counts, this occurs when photons sent by Alice never reach him and the wrong detector registers a result due to thermal fluctuation, therefore this has the same effect as the second error type, namely, Bob can register a wrong result even when he is using the correct base, this error type will be calibrated out using the same classical technique as in the second type. Identity verification • As all types of cryptography we also have the problem of Eve pretending to be Bob and getting the key instead of him. Therefore it is necessary to carry out identity verification, there are well established classical techniques however they require that Alice and Bob already have a private key, so for the first private key they need a “face to face meeting” Way do we need a single-photon source? • If Alice sends more then 1 photon at a time then it will enable Eve to reduce the error she is causing by here measurements. • For example if Alice is sending 2 photons then if Eve is detecting with the wrong base, in 50% of the times she will register on both of her detectors and know that her base was wrong therefore she will not sent anything to Bob (to Bob it would occur as random deleting), and Eve will reduce the error she is causing. Single photon source • The standard (not good) technique for making a single photon source is taking a pulse laser and attenuating it strongly so that the mean number of photons in each pulse is small. The photons from a single frequency laser have a Poisson statistic: • If we take a typical value of 0.1 (mean number or photons in each pulse) then most of the time intervals will contain no photons at all, in this case 5% of the pulses that have photons, have more then 1 • • A much better option is to use a genuine single-photon source. This source emits exactly one photon on demand, some experiments have been done with such sources but they are still to slow or inconvenient to be used in advanced systems. Therefore this research field is developing fast. Practical uses Free space quantum cryptography • In free space quantum cryptography the photons travel through the air, the telescopes are used to aim and collect the photons. • The first practical demonstration of free space quantum cryptography was made in 1992 (Bennet and Brassard) and used strongly attenuated pulses of 550 nm which traveled 0.32 meter in free air. • Today free space quantum cryptography is made across 144km. • The goal is to develop systems which will communicate with satellites. Overcoming problems of free space cryptography • Long range free space systems use wave length’s of 600-900nm which have small atmospheric losses and low noise detectors with high efficient are available. The two main sources of error’s are: • Air turbulence which cause random deviation in direction and timing, this is the same effect that cusses stars to twinkle. The errors caused by this effect can be minimized by sending a bright classical pulse in front of our signal with known properties so Bob can estimate and calibrate out this effect. • Background light: from the sun moon or artificial sources can cause false counting. This effect can be reduced by placing filters in front of the detector and switching the detector on only when the signal is expected to arrive. Quantum cryptography in Optical fibers • Optical fibers systems are in principle much more convenient then free space systems. the beam does not diverge, doesn't need a strait line between Alice and Bob ex. the two main problem of using fibers are: • Losses, signals that propagate through optical fibers lose intensity as they propagate. The three common wavelength used in fiber optics are 850, 1300 and 1550 nm, the 850 nm has the largest scattering losses of the three however this is the wave length that is used due to much better detectors available (the other two are less energetic and need detectors with a smaller band gap which have higher false count and have a high after pulsing that restricts the bit rate). • Fibers are birefringent. For laboratory uses this effect can be calibrated out as shown before, for “real world” fibers buried in the ground and suffering from high thermal and mechanical deference along the fiber which change there birefringent properties this effect is to strong, for this reason a different approach is necessary: • A common solution is using optical phase encoding: this can be done using a MachZender interferometer • For a relative phase shift of 0 or pi the photon will exit the Fiber Coupler through the 0 or 1 port, if the relative phase shift is pi/2 or 3pi/2 the photon can exit either port (50:50). • Because the last technique requires a careful balance of the two arms on the length of several km, the technique of a single long arm was developed. • This technique is also effected by small length changes in the arms as well as changes in the birefringence of the optical components. • Auto compensating single interferometer. • Bob sends a multi photon pulse to Alice. the beam passes through the FM and is attenuated to a single photon and send back along the same path, any birefringence in the first transit are compensated in the second one. • This has been done over distances of 67km. • This technique is slow due to detector saturation by the light scattered from Bobs pulse and vulnerable to ‘Trojan Horse’ • (*) Faraday rotator mirrors take the output beam from a single mode fiber and rotate the polarization by 90 degrees before sending it back through the same fiber. By doing so, a Faraday mirror functions as a phase conjugate mirror and cancels out any birefringent effects the beam experienced along the forward path. Experiments • Laser communication experiments between satellites including ground stations have been demonstrated. satellite.pdf • QKD over 144 km in Tenerife, Spain. 144KmSpain.pdf