Download Single particles quantum cryptography

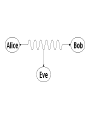
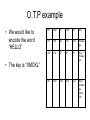
Single particles quantum
cryptography.
Barak Gur
2008
What is Cryptography
• Cryptography is hiding information so that
only the person its meant to will able to
read it .
• Cryptography, in its classical way, is
considered as branch of both mathematics
and computer science in its modern way
its pure physics.
• When we say Cryptography we mean
encryption and decryption of information.
Medieval cryptography
• The very beginning of cryptography needed no more then a pen and
paper, as most people could not read.
• then the development of cipher text started: taking a plaintext and
by using an algorithm (called cipher) we make it unreadable to
anyone except those possessing the key. For example: The first and
simplest cipher text Technique is rearranging the order of letters e.g.
'help me' becomes 'ehpl em'.
• After that came a systematically replace of letters or groups of
letters with other letters or groups of letters (e.g., 'fly at once'
becomes 'gmz bu podf' by replacing each letter with the one
following it in the alphabet). For example: An early substitution
cipher was the Caesar cipher, in which each letter was replaced by
a letter some fixed number of positions further down the alphabet. It
was named after Julius Caesar who used it, with a shift of 3, to
communicate with his generals.
religious applications
• Caesar cipher can be found in the
“Mezuza”: ‫כוזו במוכסז כוזו‬.
• 666 or in some early manuscripts, 616, is
the sum of the letters of the Roman
Emperor Nero (NERO and NERON).
Vulnerability of cipher text
Technique
• Cipher texts produced by classical ciphers
always reveals some statistical information
about the original text, which can often be used
to break them.
• An example of such use of statistical information
was the discovery of frequency analysis by
polymath al- Kindi at about the 9th century,
nearly all such simple ciphers became more or
less readily breakable by an informed attacker.
• A typical distribution of letters in English language text.
Weak ciphers do not sufficiently mask the distribution,
and this might be exploited by a cryptanalyst to read the
message.
1800 to World War 2
• In 1917 the one time pad (O.T.P) was
introduced.
• O.T.P is an encryption algorithm where the
plaintext is combined with a random key or "pad"
that is as long as the plaintext and is used only
once.
• If the key is truly random, never reused, and
kept secret, the one-time pad provides perfect
secrecy.
• In fact O.T.P is the goal of Single particles
quantum cryptography which will be discussed
later.
O.T.P example
• We would like to
encode the word
“HELLO”
23X
12M
2C
10K
11L
key
+7H
+4E
11L
11L
14O
messa
ge
= 30
=16
13
21
25
Key +
messa
ge
=4E
16Q
13N
21V
25Z
Key +
messa
ge
(mod
26)
• The key is “XMCKL”
World War 2
• The Enigma which is most known for
being used by the Nazi’s during World War
II.
• Enigma was a family of related electromechanical rotor machines.
• For a message to be correctly encrypted
and decrypted, both sender and receiver
had to set up their Enigma in the same
way.
• Mathematician Marian Rejewski, at
Poland's Cipher Bureau, in December
1932 reconstructed the German Army
Enigma, using mathematics and limited
documentation.
Modern cryptography
• Symmetric-key cryptography: encryption in
which both the sender and receiver share the
same key (the only kind of encryption publicly
known until June 1976).
• Public-key cryptography: two different but
mathematically related keys are used — a public
key and a private key.
• In public-key cryptography, the public key is
broadcasted freely (used for encryption), while
the private key remains secret (used for
decryption).
• The RSA encryption scheme used for
internet security is based on the fact that
the time taken to find the prime factors of a
large number increases exponentially with
the number of digits.
Summary
Principles of quantum cryptography
• We would like to encrypt our message with a
private key which will be used once (O.T.P)
instead of a public one.
• Quantum cryptography's purpose is to provide a
secure way for exchanging this key.
• The two basic schemes are of single particle and
entangle states, we shell discuss the first one
which is the most commonly implemented in the
field.
Quantum no cloning

A
U
e
A
e
B
B


A
e
A
B

U
B
   e B  AU U 
†
A
e
B
 
B
A

e
A
B


A

A
B

B
 
2
BB84 protocol
• The protocols can use any two pairs of
orthogonal polarization, we shell use the
following:
• Our setup is as followed:
• Bob does not know which base Alice has
chosen for the photon he will receive,
therefore he chooses his base randomly.
• In the cases he chose the same like Alice
he measured the correct answer.
• Alice also chooses her base randomly
then they will have there basses matching
for 50% of the cases.
• For the other 50% Bob is using the wrong
base and will get random results .
The way Alice and Bob work
1.
2.
3.
4.
5.
6.
7.
Alice transmits her data while choosing her basses
randomly (she isn't telling which base she chose).
Bob records the results he is receiving, he is choosing
his base randomly.
On a p.l (public line) Bob tells Alice of his Choice of
basses.
Alice compares it to her choice of basses and by p.l
tells Bob what measurements they will eliminate.
Over a p.l Bob sends Alice a subset of his results.
If Alice finds that the error rate is less then 25% they
conclude that the communication was secured.
The remaining bits are their private key.
An example of how Alice and Bob
work
Why 25% error indicates the
presence of Eve?
•
•
•
Lets say Eve is detecting the photons Alice has sent to Bob and then
transmitting a “copy” of then to Bob.
Eve is choosing her base randomly, this is the best option for her. (50% of
the cases she had the correct base and therefore transmitted the correct
answer to Bob.)
We are interested at cases in which Bob used the correct base (like Alice) at
50% of this cases Eve had the wrong base, so she transmitted using this
base. Out of this cases Bob recorded the wrong answer at 50% of the cases
(he has a 50%-50% chance to record a correct/wrong answer when he is
using a different base then Eve).
System errors
•
Even when Eve isn't present our system has errors, in order to be able to
detect Eve present it is crucial to deal with this errors.
•
First error type: Random deleting of photons (caused by
absorption/scattering or detector inefficiency), the way to coupe with is by
Bob telling Alice Which base he chose and when did he register his
result, therefore random deleting effects the efficiency of the system but
not the security.
•
Second error type: if the medium in which the photons travel is
birefringence then the polarization angle of a photon will change. The
way to calibrate this error out of the system is the same like in classical
data transmission (by using “Shannon's noisy channel coding theorem”)
we need to make sure that the error probability is much smaller then error
rate introduced by Eve.
The number of bites that must be compared to correct this error is:
•
• Third error type: detector dark counts, this occurs when photons
sent by Alice never reach him and the wrong detector registers a
result due to thermal fluctuation, therefore this has the same effect
as the second error type, namely, Bob can register a wrong result
even when he is using the correct base, this error type will be
calibrated out using the same classical technique as in the second
type.
Identity verification
• As all types of cryptography we also have
the problem of Eve pretending to be Bob
and getting the key instead of him.
Therefore it is necessary to carry out
identity verification, there are well
established classical techniques however
they require that Alice and Bob already
have a private key, so for the first private
key they need a “face to face meeting”
Way do we need a single-photon
source?
• If Alice sends more then 1 photon at a time then
it will enable Eve to reduce the error she is
causing by here measurements.
• For example if Alice is sending 2 photons then if
Eve is detecting with the wrong base, in 50% of
the times she will register on both of her
detectors and know that her base was wrong
therefore she will not sent anything to Bob (to
Bob it would occur as random deleting), and Eve
will reduce the error she is causing.
Single photon source
• The standard (not good) technique for making a single photon
source is taking a pulse laser and attenuating it strongly so that the
mean number of photons in each pulse is small. The photons from a
single frequency laser have a Poisson statistic:
• If we take a typical value of 0.1 (mean number or photons in each
pulse) then most of the time intervals will contain no photons at all,
in this case 5% of the pulses that have photons, have more then 1
•
• A much better option is to use a genuine
single-photon source. This source emits
exactly one photon on demand, some
experiments have been done with such
sources but they are still to slow or
inconvenient to be used in advanced
systems. Therefore this research field is
developing fast.
Practical uses
Free space quantum cryptography
• In free space quantum cryptography the
photons travel through the air, the
telescopes are used to aim and collect the
photons.
• The first practical demonstration of free
space quantum cryptography was made in
1992 (Bennet and Brassard) and used
strongly attenuated pulses of 550 nm
which traveled 0.32 meter in free air.
• Today free space quantum cryptography
is made across 144km.
• The goal is to develop systems which will
communicate with satellites.
Overcoming problems of free
space cryptography
• Long range free space systems use wave length’s of
600-900nm which have small atmospheric losses and
low noise detectors with high efficient are available. The
two main sources of error’s are:
• Air turbulence which cause random deviation in direction
and timing, this is the same effect that cusses stars to
twinkle. The errors caused by this effect can be
minimized by sending a bright classical pulse in front of
our signal with known properties so Bob can estimate
and calibrate out this effect.
• Background light: from the sun moon or artificial sources
can cause false counting. This effect can be reduced by
placing filters in front of the detector and switching the
detector on only when the signal is expected to arrive.
Quantum cryptography in Optical
fibers
• Optical fibers systems are in principle much more
convenient then free space systems. the beam does not
diverge, doesn't need a strait line between Alice and Bob
ex. the two main problem of using fibers are:
• Losses, signals that propagate through optical fibers
lose intensity as they propagate. The three common
wavelength used in fiber optics are 850, 1300 and 1550
nm, the 850 nm has the largest scattering losses of the
three however this is the wave length that is used due to
much better detectors available (the other two are less
energetic and need detectors with a smaller band gap
which have higher false count and have a high after
pulsing that restricts the bit rate).
• Fibers are birefringent. For laboratory uses
this effect can be calibrated out as shown
before, for “real world” fibers buried in the
ground and suffering from high thermal
and mechanical deference along the fiber
which change there birefringent properties
this effect is to strong, for this reason a
different approach is necessary:
• A common solution is using optical phase
encoding: this can be done using a MachZender interferometer
• For a relative phase shift of 0 or pi the
photon will exit the Fiber Coupler through
the 0 or 1 port, if the relative phase shift is
pi/2 or 3pi/2 the photon can exit either port
(50:50).
• Because the last technique requires a
careful balance of the two arms on the
length of several km, the technique of a
single long arm was developed.
• This technique is also effected by small
length changes in the arms as well as
changes in the birefringence of the optical
components.
• Auto compensating single interferometer.
• Bob sends a multi photon pulse to Alice.
the beam passes through the FM and is
attenuated to a single photon and send
back along the same path, any
birefringence in the first transit are
compensated in the second one.
• This has been done over distances of 67km.
• This technique is slow due to detector saturation
by the light scattered from Bobs pulse and
vulnerable to ‘Trojan Horse’
• (*) Faraday rotator mirrors take the output beam
from a single mode fiber and rotate the
polarization by 90 degrees before sending it
back through the same fiber. By doing so, a
Faraday mirror functions as a phase conjugate
mirror and cancels out any birefringent effects
the beam experienced along the forward path.
Experiments
• Laser communication experiments
between satellites including ground
stations have been demonstrated.
satellite.pdf
• QKD over 144 km in Tenerife, Spain.
144KmSpain.pdf