* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Defining Functions
Survey
Document related concepts
Transcript
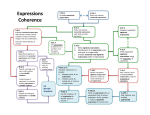
DefiningFunctions YanHuang [email protected] TheVeryBasicSyntax double :: Int ® Int double x = x + x ConditionalExpressions Asinmostprogramminglanguages,functions canbedefinedusingconditionalexpressions. takesanintegernandreturnsnif itisnon-negativeand-notherwise. abs ConditionalExpressions Asinmostprogramminglanguages,functions canbedefinedusingconditionalexpressions. abs :: Int ® Int abs n = if n ≥ 0 then n else -n takesanintegernandreturnsnif itisnon-negativeand-notherwise. abs Conditionalexpressionscanbenested: Definethefunctionsignum,whichreturns-1when givenanegativeinteger;returns1whengivena positiveinteger;and0ifgiven0. Conditionalexpressionscanbenested: signum :: Int ® Int signum n = if n < 0 then -1 else if n == 0 then 0 else 1 • InHaskell,conditionalexpressionsmustalways haveanelsebranch,whichavoidsanypossible ambiguityproblemswithnestedconditionals. GuardedEquations Asanalternativetoconditionals,functionscan alsobedefinedusingguardedequations. GuardedEquations Asanalternativetoconditionals,functionscan alsobedefinedusingguardedequations. abs n | n ≥ 0 =n | otherwise = -n Aspreviously,butusingguardedequations. Thecatchallconditionotherwise isdefinedin the“Prelude”byotherwise=True. Guardedequationscanbeusedtomakedefinitions involvingmultipleconditionseasiertoread.E.g., Trydefinesignum usingguardedequations. Guardedequationscanbeusedtomakedefinitions involvingmultipleconditionseasiertoread: signum n | n < 0 = -1 | n == 0 = 0 | otherwise = 1 PatternMatching Manyfunctionshaveaparticularlycleardefinition usingpatternmatchingontheirarguments. not :: Bool ® Bool not False = True not True = False notmapsFalsetoTrue,andTruetoFalse. Functionscanoftenbedefinedinmanydifferent waysusingpatternmatching.Forexample (&&) True True False False :: Bool ® Bool ® Bool && True = True && False = False && True = False && False = False canbedefinedmorecompactlyby True && True = True _ && _ = False Theunderscoresymbol_isa wildcard patternthatmatches anyargumentvalue. However,thefollowingdefinitionismoreefficient, becauseitavoidsevaluatingthesecondargumentif thefirstargumentisFalse: True && b = b False && _ = False z Patternsarematchedinorder.Forexample,the followingdefinitionalwaysreturnsFalse: _ && _ = False True && True = True z Youmaynotrepeat variablesinthesamepattern. Forexample,thefollowingdefinitiongivesanerror: b && b = b _ && _ = False ListPatterns Internally,everynon-emptylistisconstructed byrepeateduseofanoperator(:)called“cons” thataddsanelementtothestartofalist. [1,2,3,4] Means1:(2:(3:(4:[]))). Functionsonlistscanbedefinedusingx:xs pattern. head :: [a] ® a head (x:_) = x tail :: [a] ® [a] tail (_:xs) = xs headandtailmapanynon-emptylist toitsfirstandremainingelements. z x:xs patternsonlymatchnon-empty lists: > head [] ERROR z x:xspatternsmustbeparenthesised,because applicationhaspriorityover(:).Forexample, thefollowingdefinitiongivesanerror: head x:_ = x Scala • Fullsupportforfunctionalprogrammingwithaverystrongstatictype system,heavilyinfluencedbyHaskell - Currying - Typeinference - Immutability - Lazyevaluation - Patternmatching - Algebraicdatatypes • CompilestoJVMbytecode LambdaExpressions Functionscanbeconstructedwithoutnaming thefunctionsbyusinglambdaexpressions. lx®x+x Thenamelessfunctionthattakesa numberxandreturnstheresultx+x. z Thesymboll istheGreekletterlambda,andistypedatthe keyboardasabackslash“\”. z Inmathematics,namelessfunctionsareusuallydenoted usingthea symbol, asinxa x+x. z InHaskell,theuseofthel symbolfornamelessfunctions comesfromthelambdacalculus,thetheoryoffunctionson whichHaskellisbased. WhyAreLambda's Useful? Lambdaexpressionscanbeusedtogiveaformal meaningtofunctionsdefinedusingcurrying. Forexample: add x y = x + y means add = l x ® (l y ® x + y) Lambdaexpressionsarealsousefulwhendefining functionsthatreturnfunctionsasresults. Forexample: const :: a ® b ® a const x _ = x ismorenaturallydefinedby const :: a ® (b ® a) const x = \_ ® x Lambdaexpressionscanbeusedtoavoid namingfunctionsthatareonlyreferencedonce. Forexample: odds n = map f [0..n-1] where f x = x*2 + 1 canbesimplifiedto odds n = map (\x ® x*2 + 1) [0..n-1] Sections Anoperatorwrittenbetween itstwoargumentscanbe convertedintoacurriedfunctionwrittenbefore itstwo argumentsbyusingparentheses. Forexample: > 1+2 3 > (+) 1 2 3 Thisconventionalsoallowsoneoftheargumentsof theoperatortobeincludedintheparentheses. Forexample: > (1+) 2 3 > (+2) 1 3 Ingeneral,ifÅ isanoperatorthenfunctionsoftheform (Å),(xÅ)and(Åy)arecalledsections. WhyAreSections Useful? Usefulfunctionscansometimesbeconstructed inasimplewayusingsections.Forexample: (1+) - successorfunction (1/) - reciprocationfunction (*2) - doublingfunction (/2) - halvingfunction Exercises (1) Considerafunctionsafetail thatbehavesinthesamewayas tail,exceptthatsafetail mapstheemptylisttotheemptylist, whereastailgivesanerrorinthiscase.Definesafetail using: (a) aconditionalexpression; (b) guardedequations; (c) patternmatching. Hint:thelibraryfunctionnull::[a]® Boolcanbeusedto testifalistisempty. (2) Givethreepossibledefinitionsforthelogicalor operator(||)usingpatternmatching. (3) Redefinethefollowingversionof(&&)using conditionalsratherthanpatterns: True && True = True _ && _ = False (4) Dothesameforthefollowingversion: True && b = b False && _ = False