Download Rewriting Equations

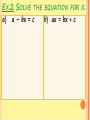
TEACHER NOTES
The warm up works on the distribution property,
but also use it to talk about un-distribution
basically going backwards factoring out the GCF.
 This will help in the Examples
 The examples are all from section 3.8 of the
Algebra 1 book and Homework is out of the
Workbook
 Slides 4, 7, and 12 are the worked out examples,
and slide 16 is the challenge problem. May want
to consider printing those out for their notebook.
We quiz Thurs., if you are behind you may want
to print all of it out to save time.
 The challenge problem comes from p.189 #37

STANDARD AND LEARNING TARGET

A.CED.A.4-1 Rearrange formulas to highlight a
quantity of interest, using the same reasoning as in
solving equations, limiting variables of interest to
linear and quadratic. For example, rearrange Ohm’s
law V = IR to highlight resistance R. *(Modeling
Standard)
I can solve literal equations using the same processes used in
solving equations.
 I can solve real-world formulas limited to linear and
quadratic variables.

WARM UP
Use the distributive property.
1. -9( x + 2)
2. ½ (8x – 7)
REVERSE: Greatest Common Factor
3. 4x - 12
4. 15x + 10
N
o
t
e
s
REWRITING
EQUATIONS
AA1.CC
WORKED OUT EXAMPLE
Which means to
solve for y with x
represented on the
other side of the =
sign as part of a
relationship
between the y and
the x.
Why is putting the equation in
this form advantageous for us
when graphing?
EX.1 SOLVE
FOR Y IN TERMS OF X.
b. 2 + 6y = 3x + 4
PRACTICE!
Solve for y in terms of x.
8x – 5x + 21 = 36 – 6y
WORKED OUT EXAMPLE
EX.2 SOLVE THE EQUATION FOR X.
a)
a – bx = c
b) ax = bx + c
Solve the
equation
for x.
PRACTICE!
ERROR ANALYSIS PRACTICE!
a)
WHY
IS THEIR ANSWER NOT CORRECT??
b)
IMPORTANT FORMULAS!
WORKED OUT EXAMPLE
EX.4 REWRITING FORMULAS!
a. Solve for t.
I = Prt
b. Solve for r.
d = rt
PRACTICE!
a. Solve for w.
b. Solve for h.
(Volume of a rectangular
prism)
(Surface area of a prism)
V = lwh
S = 2B + Ph
𝑺 − 𝟐𝑩
𝑨𝒏𝒔𝒘𝒆𝒓: 𝒉 =
𝑷
EX.5 SOLVE THE FORMULA FOR W.
The formula for
the perimeter of a
rectangle is:
Use the formula to find the width of the rectangle
shown below.
CHALLENGE!
The distance d (in miles) traveled by a
car is given by d = 55t where t is the
time (in hours) the car has traveled.
The distance d (in miles) traveled is also
given by d = 20g where g is the number
of gallons of gasoline used by the car.
Write an equation that expresses g as a
function of t.
HOMEWORK
Red Workbook
p.44-45
#2-12 even; 13-19 all