Download Math 2 Geometry Definition Polygon Examples Not Polygons

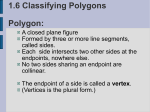
Definition
Math 2 Geometry
Based on Elementary Geometry, 3rd ed, by Alexander & Koeberlein
2.5
Convex Polygons
A polygon is a closed plane figure whose
sides are line segments that intersect only
at the endpoints.
In this text only: convex polygons
(interior angles measure from 0° to 180°)
Examples?
Polygon Examples
Not Polygons
Convex
Polygons
Concave Polygons
Classify by number of sides
Triangle
(3)
Quadrilateral (4)
Pentagon
(5)
Classify by number of sides
Hexagon (6)
Heptagon (7)
Octagon (8)
1
Classify by number of sides
Informal Definition
A diagonal of a polygon is a line segment
that joins two nonconsecutive vertices.
Nonagon (9)
B
Decagon (10)
A
C
E
D
Theorem 2.5.1
The total number of diagonals D in a
polygon of n sides is given by the formula:
D=
n (n − 3)
2
Theorem 2.5.2
The sum S of the measures of the interior
angles of a polygon with n sides is given by:
S = (n – 2) 180°
•
Use the formula to find the number of
diagonals of:
•
a triangle
•
a quadrilateral
•
a pentagon
D=
n (n − 3)
2
Informal Definitions
• Equiangular polygon: All angles are
congruent.
• Equilateral polygon: The measure of all
sides are equal.
2
Definition
A regular polygon is a polygon that is both
equilateral and equiangular.
Not Regular Polygons
Notice it is possible for Polygons to be either
equilateral or equiangular but not both.
Notice: A square is a regular quadrilateral.
Rectangle
Rhombus
Corollary 2.5.3
The measure I of each interior angle of a
regular polygon of n sides is:
I=
Corollary 2.5.4
The sum of the four interior angles of a
quadrilateral is 360°
(n − 2) ⋅180
n
Corollary 2.5.5
The sum of the measures of the exterior
angles of a polygon, one at each vertex, is
360°.
Corollary 2.5.6
The measure E of each exterior angle of a
regular polygon of n sides is:
E=
360
n
3
Informal Definition
A polygram is the star-shaped figure that
results when the sides of certain polygons
are extended.
Pentagram
Hexagram
4