Download PowerPoint

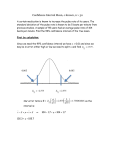
Statistics
Statistics:
1
1. Model
X i ~ N (  ,  2 ), i  1, 2,  , n iid.
2. Estimation
ˆ  x ,
3. Hypothesis test
   0 ,  2   02
ˆ 2  s 2
lecture 7
Estimation
Estimat
Definition:
^
A (point) estimate  of a parameter, , in the model is a
“guess” at what  can be (based on the sample). The
^
corresponding random variable Q
is called an estimator.
Population




2

Sample
...
...
^

parameter
estimat
estimator

ˆ  x
X

ˆ 2  s 2
S2
lecture 7
Estimation
Unbiased estimate
Definition: ^
An estimator Q is said to be unbiased if
^
E(Q) = 
We have
E( X )  
unbiased
E ( S 2 )   2 unbiased
3
lecture 7
Confidence interval for the
mean
Example:
In a sample of 20 chocolate bars the amount of calories
has been measured:
• the sample mean is 224 calories
How certain are we that the population mean  is close
to 224?
The confidence interval (CI) for  helps us here!
4
lecture 7
Confidence interval for 
Known variance
Let x be the average of a sample consisting of n observations
from a population with mean  and variance 2 (known).
A (1-)100% confidence interval for  is given by
x  z / 2 
n
   x  z / 2 
n
From the standard normal distribution N(0,1)
•We are (1-)100% confident that the unknown parameter  lies in the CI.
•We are (1-)100% confident that the error we make by using x as an
estimate of  does not exceed z / 2  n (from which we can find n for a
given error tolerance).
5
lecture 7
Confidence interval for 
Known variance
Confidence interval for known variance is a results of the
Central Limits Theorem. The underlying assumptions:
• sample size n > 30, or
• the corresponding random var. is (approx.) normally
distributed
(1 - )100% confidence interval :
• typical values of :  =10% ,  = 5% ,  = 1%
• what happens to the length of the CI when n increases?
6
lecture 7
Confidence interval for 
Known variance
Problem:
In a sample of 20 chocolate bars the amount of calories has
been measured:
• the sample mean is 224 calories
In addition we assume:
• the corresponding random variable is approx. normally
distributed
• the population standard deviation  = 10
Calculate 90% and 95% confidence interval for 
Which confidence interval is the longest?
7
lecture 7
Confidence interval for 
Unknown variance
Let x be the mean and s the sample standard deviation of a
sample of n observations from a normal distributed population
with mean  and unknown variance.
A (1-)100 % confidence interval for  is given by
x  t / 2, n 1 s
n
   x  t / 2, n1 s
n
From the t distribution with n-1 degrees of freedom t(n -1)
•Not necessarily normally distributed, just approx. normal distributed.
•For n > 30 the standard normal distribution can be used instead of the t
distribution.
•We are (1-)100% confident that the unknown  lies in the CI.
8
lecture 7
Confidence interval for 
Unknown variance
Problem:
In a sample of 20 chocolate bars the amount of calories
has been measured:
• the sample mean is 224 calories
• the sample standard deviation is 10
Calculate 90% and 95% confidence intervals for 
How does the lengths of these confidence intervals
compare to those we obtained when the variance was
known?
9
lecture 7
Confidence interval for 
Using the computer
MATLAB: If x contains the data we can obtain a (1-alpha)100%
confidence interval as follow:
mean(x) + [-1 1] * tinv(1-alpha/2,size(x,1)-1) *
std(x)/sqrt(size(x,1))
where
•size(x,1) is the size n of the sample
•tinv(1-alpha/2,size(x,1)-1) = t/2(n-1)
•std(x) = s (sample standard deviation)
R:
mean(x) + c(-1,1) * qt(1-alpha/2,length(x)-1) *
sd(x)/sqrt(length(x))
10
lecture 7
Confidence interval for
2

Example:
In a sample of 20 chocolate bars the amount of
calories has been measured:
• sample standard deviation is10
How certain are we that the population variance 2
is close to 102?
The confidence interval for  helps us answer this!
2
11
lecture 7
Confidence interval for 2
Let s be the standard deviation of a sample consisting of n
observations from a normal distributed population with
variance 2.
A (1-) 100% confidence interval for  is given by
2
(n  1) s 2
2 / 2, n 1
 2 
(n  1) s 2
12  / 2, n 1
From 2 distribution with n-1 degrees of freedom
2
We are (1-)100% confident that the unknown parameter  lies in the CI.
12
lecture 7
Confidence interval for 2
Problem:
In a sample of 20 chocolate bars the amount of
calories has been measured:
• sample standard deviation is10
Find the 90% and 95% confidence intervals for 2
13
lecture 7
Confidence interval for 2
Using the computer
MATLAB: If x contains the data we can obtain a (1-alpha)100%
confidence interval for 2 as follow:
(size(x,1)-1)*std(x)./
chi2inv([1-alpha/2 alpha/2],size(x,1)-1)
R:
(length(x)-1)*sd(x))/
qchisq(c(1-alpha/2,alpha/2), length(x)-1)
14
lecture 7
Maximum Likelihood Estimation
The likelihood function
Assume that X1,...,Xn are random variables with joint
density/probability function
f ( x1 , x2 ,, xn ; )
where  is the parameter (vector) of the distribution.
Considering the above function as a function of  given
the data x1,...,xn we obtain the likelihood function
L( ; x1 , x2 ,, xn )  f ( x1 , x2 ,, xn ; )
15
lecture 7
Maximum Likelihood Estimation
The likelihood function
Reminder: If X1,...,Xn are independent random variables
with identical marginal probability/ density function f(x;),
then the joint probability / density function is
f ( x1 , x2 ,, xn ; )  f ( x1; ) f ( x2 ; ) f ( xn ; )
Definition: Given independent observations x1,...,xn from
the probability / density function f(x;) the maximum
likelihood estimate (MLE)  is the value of  which
maximizes the likelihood function
L( ; x1 , x2 ,, xn )  f ( x1; ) f ( x2 ; ) f ( xn ; )
16
lecture 7
Maximum Likelihood Estimation
Example
Assume that X1,...,Xn are a sample from a normal
population with mean  and variance 2. Then the
marginal density for each random variable is
 1
2
f ( x; ) 
exp  2 x    
2
 2

2
1
Accordingly the joint density is
1
 1
2
f ( x1 , x2 ,, xn ; ) 
exp  2  xi    
n2
2 n2
(2 ) ( )
 2 i

The logarithm of the likelihood function is
n
n
1
2
2
2
ln L(  ,  ; x1 , x2 ,, xn )   ln( 2 )  ln(  )  2  xi   
2
2
2 i
17
lecture 7
Maximum Likelihood Estimation
Example
We find the maximum likelihood estimates by maximizing
the log-likelihood:

1
2
ln L(  ,  ; x)  2  xi     0

 i
1
which implies ̂   xi  x . For 2 we have
n i

n
1
2
2


ln
L
(

,

;
x
)



x


0
i
2 
2
2
2

2
2  i
1
2
2
which implies ˆ   xi  x 
n i
n 1 2
2
Notice E[ˆ ] 
 , i.e. the MLE is biased!
n
18
lecture 7