* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 8th Math Unit 3 - Livingston County School District
Corecursion wikipedia , lookup
Renormalization group wikipedia , lookup
Mathematical optimization wikipedia , lookup
Inverse problem wikipedia , lookup
Plateau principle wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Linear algebra wikipedia , lookup
Mathematical descriptions of the electromagnetic field wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Routhian mechanics wikipedia , lookup
Least squares wikipedia , lookup
Simplex algorithm wikipedia , lookup
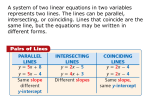
Livingston County Schools Eighth Math Unit 3 Graphing Linear Equations & System of Equations Unit Overview Students grasp the concept of a function as a number that assigns to each input exactly one output. Students use the equations y=mx+b to interpret a line for slope and y-intercept. Students solve system of 2 linear equations and relate them to pairs of lines in the plane. Length of unit: 45 days KY Core Academic Standard Learning Target K 8.EE.5 Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. For example, compare a distance-time graph to a distance-time equation to determine which of two moving objects has greater speed. 8.EE.6 Use similar triangles to explain why the slope m is the same between any two distinct points on a nonvertical line in the coordinate plane; derive the equation y=mx for a line through the origin and the equation y=mx+b for a line 22. I can graph proportional relationships Reasoning Targets 23. I can compare two different proportional relationships represented in different ways. (For example, compare a distance-time graph to a distance-time equation to determine which of two moving objects has greater speed.) 24. I can interpret the unit rate of proportional relationships as the slope of the graph. X 25. I can identify characteristics of similar triangles. 26. I can find the slope of a line. 27. I can determine the yintercept of a line. (Interpreting unit rate as the slope of the graph is included in 8.EE.) Reasoning Targets 28. I can analyze patterns for points on a line through the origin. X R X S P Critical Vocabulary Texts/Resources/Activities constant of proportionality, direct proportion, origin, proportion, slope-intercept form, unit price, unit rate, yintercept Crosswalk Lesson 13 and 14 Origin, rate, ratio, rate of change, slope, slope intercept form, yintercept Crosswalk Lesson 11 X X X X intercepting the vertical axis at b. 8.EE.8a Analyze and solve pairs of simultaneous linear equations: a. Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously. 8.EE.8b Analyze and solve pairs of simultaneous linear equations: b. Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the 29. I can derive an equation of the form y = mx for a line through the origin. 30. I can analyze patterns for points on a line that do not pass through or include the origin. 31. I can derive an equation of the form y=mx + b for a line intercepting the vertical axis at b (the yintercept). 32. I can use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane. 38. I can identify the solution(s) to a system of two linear equations in two variables as the point(s) of intersection of their graphs. 39. I can describe the point(s) of intersection between two lines as points that satisfy both equations simultaneously. 40. I can define “inspection”. 41. I can identify cases in which a system of two equations in two unknowns has no solution 42. I can identify cases in which a system of two equations in two unknowns has an infinite number of solutions. 43. I can solve a system of two X X X X X X X X X Coefficient, system of linear equations Crosswalk Lesson16 equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6 8.EE.8c Analyze and solve pairs of simultaneous linear equations: c. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair. 8.F.1 Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output equations (linear) in two unknowns algebraically. 44. I can solve simple cases of systems of two linear equations in two variables by inspection. Reasoning Targets 45. I can estimate the point(s) of intersection for a system of two equations in two unknowns by graphing the equations. 46. I can solve systems of two linear equations in two unknowns. 47. I can define the term “system of equation” and “simultaneous linear equations”. Reasoning Targets 48. I can apply rules for solving systems of two equations in two unknowns to mathematical problems. 49. I can analyze real-world problems that lead to two linear equations in two variables by extracting needed information and translating words to symbols. X 50. I can examine the correspondence or relationship between input and output values in a set of ordered pairs and identify functions as those for which each input has only one output. 51. I can recognize the graph of a function as a set of ordered pairs consisting of an input value and the corresponding output value. X X X X Coefficient, substitution, elimination Crosswalk Lesson 17-18 Dependent variable, function, independent variable, nonlinear function, domain, range, rule, vertical line test Crosswalk Lesson 19 Lesson 3-4 p. 134 Functions X X X X 8.F.2 Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change. 8.F.3 Interpret the equation y=mx+b as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function A=s2 giving the area of a square as a function of its side length is not linear because its graph contains the points (1,1), (2,4), and (3,9), which are not on a straight line. 52. I can identify functions algebraically including slope and y intercept. 53. I can identify functions using graphs. 54. I can identify functions using tables. 55. I can identify functions using verbal descriptions Reasoning Targets 56. I can compare and Contrast 2 functions with different representations. 57. I can draw conclusions based on different representations of functions. X 58. I can recognize that a linear function is graphed as a straight line. 59. I can recognize the equation y=mx+b is the equation of a function whose graph is a straight line where m is the slope and b is the y-intercept. 60. I can provide examples of nonlinear functions using multiple representations. Reasoning Targets 61. I can compare the characteristics of linear and nonlinear functions using various representations. X X X X Dependent variable, function, independent variable, nonlinear function, domain, range, rule, vertical line test Crosswalk Lesson 23 Lesson 3-5 p. 138 Equations, Tables, and Graphs WT ?? dependent variable, function, independent variable, linear function, nonlinear function, rate of change, relation, rule, vertical line test, Crosswalk Lesson 19-20 X X X X X 8.F.4 Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x,y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of a situation it models, and in terms of its graph or a table of values. 62. I can recognize that slope is determined by the constant rate of change. 63. I can recognize that the yintercept is the initial value where x=0. 64. I can determine the rate of change from two (x,y) values, a verbal description, values in a table, or graph. 65. I can determine the initial value from two (x,y) values, a verbal description, values in a table, or graph. Reasoning Targets 66. I can construct a function to model a linear relationship between two quantities. 67. I can relate the rate of change and initial value to real world quantities in a linear function in terms of the situation modeled and in terms of its graph or a table of values. Common Assessments Developed (Proposed Assessment Dates): X Dependent variable, function, independent variable, nonlinear function, domain, range, rule, vertical line test, rate of change X X X X X HOT Questions: Crosswalk Lesson 21