Download Simple Harmonic Motion (SHM)

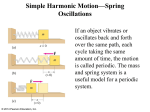
Chapter 11
Simple Harmonic Motion and
Oscillations
© 2014 Pearson Education, Inc.
Spring Oscillations - Review
Equilibrium position
Periodic Motion - If an object vibrates or
oscillates back and forth on a frictionless surface
with each cycle taking the same amount of time
and covering the same distance.
Follow’s Hooke’s Law:
The minus sign on the force indicates that it is a
restoring force—it is directed to restore the mass
to its equilibrium position.
Energy:
Us = ½ kx2
© 2014 Pearson Education, Inc.
If the mass is at the limits of its motion, the energy is all
potential.
If the mass is at the equilibrium point, the energy is all
kinetic.
PE and KE are transforming at all other points
© 2014 Pearson Education, Inc.
If the spring is hung
vertically, the only
change is in the
equilibrium position,
which is at the point
where the spring
force equals the
gravitational
force.
Spring Oscillations Vocab
• Displacement (x) is measured from the
equilibrium point
• Amplitude (A) is the maximum displacement
• A cycle is a full to-and-fro motion; this figure
shows a full cycle
• Period (T) is the time required to complete one
cycle
• Frequency (f) is the number of cycles completed
per second
© 2014 Pearson Education, Inc.
Simple Harmonic Motion (SHM)
Any vibrating system where the restoring force is proportional to the
negative of the displacement is in SHM, and is often called a simple
harmonic oscillator. Must be in the absence of friction and drag.
(11-1)
Examples: Oscillating springs, pendulums, vibrating floors, musical
instruments
© 2014 Pearson Education, Inc.
Energy in Simple Harmonic Motion
The total energy is ½ kA2
We can find the velocity at any point along the path
KE
© 2014 Pearson Education, Inc.
Us
Total Energy (all PE)
The Period and Position vs Time of SHM
• Period (T) = time of one cycle (seconds/cycle)
• Frequency (f) = cycles per second
s
Slightly different on equation sheet
© 2014 Pearson Education, Inc.
SHM is sinusoidal because the position (x) varies as a
sinusoidal function of time
By changing our reference point, we see that a rotating
object is exhibiting SHM
This allows us to define a position as a function of time for
SHM
On equation sheet
Calculator must
be in
RADIANS!!!!!!!!
t=0 is at A
© 2014 Pearson Education, Inc.
Pendulums
Pendulums undergo nearly perfect SHM.
The restoring force is F = -mg sin θ
(proportional to sin θ and not to θ itself)
If the angle is small, sin θ ≈ θ, so nearly perfect SHM
Calculator in degrees
like normal!!
© 2014 Pearson Education, Inc.
The period and frequency of a Pendulum is independent
of amplitude if θ is small and independent of mass
p
© 2014 Pearson Education, Inc.
Practice Problems
Exercise A. A mass is oscillating on a frictionless surface at the end of a
horizontal spring. Where is the acceleration zero?
a) x=-A b)x=0 c)x=+A d)at both –A and +A e)nowhere
F=kx
Answer: b
© 2014 Pearson Education, Inc.
Practice Problems
Exercise B. How much time does it take an oscillating mass with a
frequency of 1.25Hz to complete 100 oscillations?
11-2. Which of the following force displacement relationships would cause
an object to move in SHM?
a) F=-0.5x2
b)F=-2.3y c)F=8.6x
d)F=-40θ
© 2014 Pearson Education, Inc.
Practice Problems
11-3. Suppose a spring-mass system is stretched twice as far as it was
before so that the amplitude is now 2A.
I. What happens to the energy of the system?
a) Doubles b) Cuts in half c) Quadruples d) Stays the same
II. What happens to the maximum velocity of the oscillating mass?
a) Doubles b) Cuts in half c) Quadruples d) Stays the same
III. What happens to the maximum acceleration of the oscillating mass?
a) Doubles b) Cuts in half c) Quadruples d) Stays the same
© 2014 Pearson Education, Inc.
Practice Problems
11-4. A spring stretches 0.150m when a 0.300kg mass is gently suspended
from it. A) what is the spring constant, k?
b) The spring and mass are now placed on a frictionless table. The spring is
stretched 0.100m from equilibrium and released from rest. What is the
amplitude, A?
c)What is the magnitude of the maximum velocity?
© 2014 Pearson Education, Inc.
Practice Problems
11-5. With the same simple harmonic oscillator as the previous problem
where k=19.6N/m and A = 0.100m, determine a) the total energy of the
system, b) the kinetic and potential energies at x=1/2A.
© 2014 Pearson Education, Inc.
Practice Problems
11-8. Modified. An object oscillates of 1.20m to return to its beginning
position in 0.79s. A)What is the amplitude? B) What is the frequency?
C) What is the position, x at t=0.198s? D)What is the position, x at t=0.395s?
© 2014 Pearson Education, Inc.