* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.5b Notes - Jessamine County Schools
Two-body Dirac equations wikipedia , lookup
Equations of motion wikipedia , lookup
Schrödinger equation wikipedia , lookup
Exact solutions in general relativity wikipedia , lookup
Dirac equation wikipedia , lookup
Differential equation wikipedia , lookup
Partial differential equation wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Calculus of variations wikipedia , lookup
Itô diffusion wikipedia , lookup
Van der Waals equation wikipedia , lookup
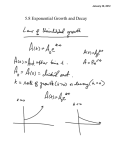
3.5 – Exponential and Logarithmic Growth Models Law of uninhibited growth or decay, where represents the original amount (when t = 0) and t represents time. (where growth happens when k > 0 and decay happens when k < 0) Uninhibited Growth of Cells - Gives the number N of cells in the culture after a time t has passed, where is the initial number of cells and k is a positive constant that represents the growth rate of the cells Ex) A colony of bacteria grows according to the law of uninhibited growth measured in grams and t is measured in days. (a) (b) (c) (d) (e) , where N is Determine the initial amount of the bacteria What is the growth rate of the bacteria? What is the population after 5 days? How long will it take for the population to reach 140 grams? What is the doubling time of the population? (a) The initial amount of bacteria, , is obtained when t = 0. (Can also be found knowing that 100 represents the initial quantity in the equation) (b) The k value represents the growth rate of the bacteria. Since k = 0.045, the growth rate is 4.5% (c) The population after 5 days is (d) For the population to reach 140 grams, N(t) = 140. Set up the equation and solve. Set up equation Divide both sides by 100 Take ln of both sides Power rule and fact that ln e = 1 Divide by 0.045 (e) The population doubles when N(t) = 200 grams, so we solve this equation. Set up equation Divide by 100 Power Rule and fact ln e = 1 Divide by 0.045 Radioactive Decay - The amount A of a radioactive material present at a a time t, where is the original amount of the radioactive material and k is a negative number that represents the rate of decay. , where k < 0 Note: all radioactive substances have a specific half-life, which is the time required for half of the radioactive substance to decay. Ex) Traces of burned wood along with ancient stone tools in an archeological dig in Chile were found to contain approximately 1.67% of the original amount of carbon 14. (a) If the half-life of carbon 14 is 5600 years, approximately when was the tree cut and burned? (a) Using the decay formula, the amount of carbon 14 present at time t can be determined by the fact that the half-life of carbon 14 is 5600 years. Substitute into formula Divide by Power Rule and fact ln e = 1 Gives us the rate of decay This means the actual decay equation is Since there is 1.67% of the original amount of carbon 14 left, we know that we have 0.0167 . Using this fact, set up an equation and solve. Set up the new equation with calculated k value Divide both sides by Rewrite as logarithm Newton’s Law of Cooling - States that the temperature of a heated object decreases over time toward the temperature of the surrounding medium. - The temperature u of a heated object at a given time t, where T is the constant temperature of the surrounding medium and is the initial temperature of the heated object and k is a negative constant. , where k < 0 Ex) An object is heated to temperature is (degrees Celsius) and is then allowed to cool in a room whose air . (a) If the temperature of the object is (a) Using the formula with T = 30 and after 5 minutes, when will it’s temperature be , the temperature of the object at time t (in minutes) is In order to find k, we use the fact that u = 80 and t = 5 Substitute into formula Subtract 30 Divide by 70 Power Rule and fact ln e = 1 Gives us the rate of cooling This means the actual cooling equation is We want to find t when u = . Using this fact, set up an equation and solve. Set up the new equation with calculated k value Subtract 30 Divide by 70 Power Rule and fact ln e = 1 ?