Download General theory of relativity

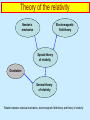
Cosmology
Syllabus
--------------------------------------------------------------------------------------------------------------------Special theory of relativity.
General theory of relativity.
Friedmann universe models, Hubble constant, cosmological red shift
Elementary particles and interactions.
Modern cosmology, phases and processes near after the Big Bang.
Evolution of the Universe with dark matter and dark energy.
---------------------------------------------------------------------------------------------------------------------
Cosmology
The study of the Universe at large, its origins and evolution. It is distinct from cosmogony,
which is the study of the origin and evolution of objects within the Universe, such as galaxies.
Although the roots of cosmology can be traced back to ancient myths and legends, and the
Greek study of the way the planets move, modern cosmology is essentially a mathematical
description of the behaviour of spacetime on the largest scale, using equations derived from
Albert Einstein’s general theory of relativity. So the date on which modern cosmology was born
can be set very precisely, as 1917, the year Einstein first applied those equations to describe
the Universe at large.
Although some theorists have developed alternative theories of gravity and spacetime, which
have led to cosmological models different from those derived from Einstein’s theory, these
alternative cosmologies have now been ruled out by observations. Within the framework of
Einstein’s theory, there have been two great cosmological hypotheses, the Big Bang and the
Steady State.
Both these models conform to the observational evidence that the Universe is expanding as
spacetime stretches, but in the big bang model this is seen as evidence that the Universe was
born out of singularity a finite time ago, while in the Steady State model it was required that
new matter should be created continuously to fill the gap between the galaxies as they moved
apart, so that the overall appearance of the Universe stayed the same.
Cosmology
The simple Steady State hypothesis has been found to be incorrect, because there is now
clear observational evidence that the Universe changes as time passes. This leaves a variety
of possible Big Bang models, which can be considered as possible descriptions of the real
Universe. To within the limits of observational accuracy, our Universe is indistinguishable from
flat model which obeys the laws of Euclidean geometry. This is the simplest possible Universe
allowed by Einstein’s equations.
Theory of the relativity
Newton’s
mechanics
Electromagnetic
field theory
Special theory
of relativity
Gravitation
General theory
of relativity
Relation between classical mechanics, electromagnetic field theory and theory of relativity
Special theory of relativity
Special theory of relativity:
Description of the relationship and interactions between moving object, developed by Albert
Einstein early in the 20th century. The theory was first published in 1905, in a mathematical form
based on equations; its implications can be more clearly visualized, however, using a
geometrical description of events taking place In a fourdimensional spacetime, first applied in
this context by Herman Minkowski in 1908. The “special” theory gets its name because it applies
only to be the special case of objects moving at constant speeds in straight lines – that is, at
constant velocities. It does not deal with accelerated motions, including the acceleration caused
by gravity. The later extensions of Einstein’s theory to deal with gravity and other accelerations
(the general theory of relativity) developed the geometrical model of spacetime further.
The key features of the special theory are that, from the point of view of an observer who is
regarded as stationary (in his or her own inertial frame), time recorded on a moving clock will
run slow, a moving object will shrink in the direction of motion, and the moving object will
gain mass. The speed of light is the same for any observer in any inertial frame, no matter how
he or she is moving relative to the source of the light, and it is impossible to accelerate an object
from below the speed of light up to the speed of light. All of these predictions have been tested
and verified many times in experiment. It is the special theory that says that mass and energy
can be interchanged in line with Einstein’s equation E0 = m0c2; this too has been confirmed by
experiments.
General theory of relativity
General theory of relativity:
Theory of gravity developed by Albert Einstein in the early part of the 20th century, and presented
to the Prussian Academy of Sciences in 1915. Because gravity is the dominant force in the
universe at large (thanks to its very long range), the theory is also a theory of cosmology, and
underpins all modern models of how the Universe got to be the way it is.
Einstein’s special theory of relativity, published in 1905, deals with the dynamical relationships
between objects moving at constant speeds in straight lines. It does not deal with accelerations,
or with gravity, which is why it is called the “special” (meaning “restricted”) theory. Einstein
always intended to generalize his theory to deal with accelerations and gravity, but it took him ten
years (not all the time devoted exclusively to the general theory) to find a satisfactory
mathematical description of the dynamics of the Universe and everything in it.
Indeed, the whole point about Einsteins’s theory is that it gives us a physical picture of how
gravity works; Isaac Newton discovered the inverse square law of gravity, but explicitly said that
he offered no explanation of why gravity should follow an inverse square law. The general theory
of relativity also says that gravity obeys an inverse square law (except in extremely strong
gravitational fields), but it tells us why this should be so. That is why Einstein’s theory is better
than Newton’s even thought it includes Newton’s theory within itself, and gives the same
“answers” as Newton’s theory everywhere except where the gravitational field is very strong.
Practices, demonstrations
Practices in special theory of relativity
- Lorentz’s transformation, Lorentz’s matrix, relativistic factor, …
Practices in general theory of relativity
- description of the curved spacetime, metric tensor, Schwarzschild’s solution, …
some demonstrations:
http://demonstrations.wolfram.com/SchwarzschildSpaceTimeEmbeddingDiagram/
http://demonstrations.wolfram.com/GravitationVersusCurvedSpacetime/
http://demonstrations.wolfram.com/BendingOfLightByAStar/
General theory of relativity
Observed effects of general theory of relativity:
 advance of perihelion
• of Mercury
• of binary pulsars
 deflection of light
• by Sun, observed first in 1919 by Arthur Eddington
• gravitational lensing, from stars (low probability) and galaxies – often observed
 gravitational time dilatation
• gravitational redshift – direct observed by Pound & Rebka experiment
• atomic clock shift by flight experiments
• GPS … in fact permanent operating general relativity experiment
 gravitational radiation
• indirect observations in binary pulsars
General theory of relativity
Advance of perihelion of Mercury
The orbit of Mercury around the Sun does not trace out the same path every time, but shifts
slightly from one orbit to the next. Each orbit is an ellipse, with the Sun at one focus of the
ellipse. In each orbit, at the closest approach of Mercury to the Sun (perihelion), the ellipse shifts
sideways by a tiny amount. This advance of the perihelion was predicted by Albert Einstein’s
general theory of relativity but cannot be explained by Isaac Newton’s theory of gravity.
The perihelion precession of Mercury is 5600 arc seconds per century. Newtonian mechanics,
taking into account all the effects from the other planets, predicts a precession of 5557 seconds
of arc per century. In the early 20th century, Albert Einstein’s General Theory of Relativity
provided the explanation for the observed precession. The effect is very small: the Mercurian
relativistic perihelion advance excess is just 42.98 arcseconds per century, similar, but much
smaller, effects operate for other planets: 8.62 arcseconds per century for Venus, 3.84 for Earth,
1.35 for Mars (http://en.wikipedia.org/wiki/Mercury_(planet))
In 1859, the French mathematician and astronomer Urbain Le Verrier reported that the slow precession of
Mercury’s orbit around the Sun could not be completely explained by Newtonian mechanics and perturbations
by the known planets. He suggested, among possible explanations, that another planet (or perhaps instead a
series of smaller 'corpuscules') might exist in an orbit even closer to the Sun than that of Mercury, to account
for this perturbation. (Other explanations considered included a slight oblateness of the Sun.) The success of
the search for Neptune based on its perturbations of the orbit of Uranus led astronomers to place faith in this
possible explanation, and the hypothetical planet was even named Vulcan. However, no such planet was ever
found. (http://en.wikipedia.org/wiki/Mercury_(planet))
General theory of relativity
Deflection of light
One of first key tests of the general theory of relativity which predicted that light from a distant
star passing close by the Sun would be “bent” by a certain amount. The only way to observe this
is during an eclipse, when the bright light of the Sun itself is blocked by the Moon, and stars can
be seen on the sky around the eclipsed Sun.
Albert Einstein published his paper predictihg this effect in 1916, abd British astronomer Arthur
Eddington organiyed an expedition to observe the eclipse from Principe, off the west coast of
Africa, while a second team observed it from Brazil. Photographs of the positions of the stars
near the Sun on the sky were then compared with photographs of the same part of the sky taken
6 months earlier, when the Earth was on the other side of the Sun in its orbit and those stars
were visible at night. The comparison showed that the stars photographed during the eclipse
seemed to have been shifted sideways slighthly by the deflection of light – by exactly the amount
that Einstein had predicted.
In principle, this deflection occurs whenever light passes near a massive object, although usually
the effect is too small to be measurable. It is caused by the curvature of spacetime associated
with the mass. A more extreme version of the same effect causes the gravitational lens
phenomenon, and in the ultimate extreme light is trapped completely within a black hole.
General theory of relativity
Gravitational time dilatation, gravitational red shift
Slowing down of clocks caused by a gravitational field, as predicted by
the general theory of relativity.


 2

c
ω2
ω1
Φ1
Φ2
(linear approximation)
With this effect must be for example calculated also by GPS navigation system
ω1 = 10,23000000000 MHz ω2 = 10,22999999543 MHz (also included effect of special
theory of relativity – transversal Doppler shift).
General theory of relativity
Binary pulsars
A binary pulsar exists when two neutron stars, one of which is a pulsar, are in orbit around one
another, forming a binary star system. The term is also used to refer to a pulsar in orbit about
any other star: for example, a white dwarf. More than twenty binary pulsars are now known, but
astronomers reserve the term “the binary pulsar” for the first one to be discovered, which is also
known by its catalogue number, as PSR 1913+16. This pulsar has provided the most accurate
test yet of Albert Einstein’s general theory of relativity, and is the most accurate clock yet
discovered.
The binary pulsar was discowered in 1974 by Russell Hulse and Joseph Taylor, of the University
of Massachusetts, working in the Arecibo radio telescope in Puerto Rico.
Measured effects:
• advance of the perihelion
• time dilatation (STR effect)
• losing energy as a result of gravitational radiation
Fro this results Hulse and Taylor won the 1993 Nobel Prize in Physics.
For other information see http://en.wikipedia.org/wiki/PSR_B1913%2B16
Equivalence principle
Equivalence principle
Acceleration is equivalent to a uniform gravitational field
That the effects of acceleration are indistinquishable from the effects of a uniform gravitational
field. This equivalence results from the equivalence between gravitational mass and inertial
mass. It led Albert Einstein to the development of general theory of relativity, when he realized
that a person falling from a roof would not feel the effects of gravity – the acceleration of their
fall would exactly cancel out the feeling of weight.
In modern language, the equivalence is best described in
terms of a spaceship being accelerated through space by
constant firing of its rocket motors. When the motors are
not firing, everything inside the spaceship floats about in
free fall, just as weightless as the person falling from a
roof. In principle, the acceleration of the rocket could be
adjusted so that everything inside felt a force exactly as
strong as the force of gravity on Earth (or any other
strength you chose), pushing things to the back of the
vehicle as it moved forward through space. Any scientific
experiments carried out in this accelerating frame of
reference would give exactly the same results as if the
spaceship were standing on its launch pad on Earth, and
not accelerating at all.
Schwarzschild metric
Eukleidian metric in kartesian and polar coordinates
ds 2  dx 2  dy 2  dz 2  dr 2  r 2 sin 2 d 2  r 2 d 2  dr 2  r 2d  2
Schwarzschild metric (space out of spherical symetrical spread matter)
ds 2  c 2 dt 2  dr 2  r 2 d  2
Minkowski metric in polar coordinates (space without matter or in special theory of relativity)

ds 2  c 2 1 
rg
r

dt 2 
dr 2
1
rg
r
 r 2d  2
Where
GM
rg  2
c
is the Schwarzschild
radius.
You can see that the Minkowski metric is limit of the Scwarzschild metric for for r >> rg.
Friedman metric
Friedman metric (space with matter regularry spreded – with constant density)
 dr 2
2
2
ds  c dt  R(t ) 
 r d 
2
1  kr

2
2
2
GM
rg  2
c
You can see that the Minkowski metric is limit of the Scwarzschild metric for for r >> rg.
The final test
… will take place the last week of semester, on Tuesday 17.5.2001 at 16:15 after the last
lecture, during the time for practise in the room T2:C2-81.
Later you can only arrange the alternative date and time of the final test with me
individually
For other information see
http://www.aldebaran.cz/~zacek/education/astrophysics_final_test.html
12 questions, each have 4 possibilities, maximum gain is 48 points,
in per cent
in points
Grading scale
from
to
from
to
Excellent (A)
90%
100%
43
48
Very good (B)
80%
90%
38
42
Good (C)
70%
80%
33
37
Satisfactory (D)
60%
70%
28
32
Sufficient (E)
50%
60%
24
27
Fail (F)
0%
50%
0
23