* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction to data mining - Laboratoire d`Infochimie
Survey
Document related concepts
Transcript
Introduction to data mining
G. Marcou+
+Laboratoire
d’infochimie, Université de Strasbourg, 4, rue Blaise
Pascal, 67000 Strasbourg
1
Motivation of data mining
Discover automatically useful information in large
data repository.
Extract patterns from experience.
Predict outcome of future observations.
Learning:
Experience
Set of Task
Preformance Measure
If Experience increase, performance measure on the set of tasks increases
Organisation of data
Datasets are organized as instances/attributes
Instances
Synonyms
Data points
Entries
Sample
…
Attributes
Synonyms
Factors
Variables
Measures
...
Nature of data
Attributes can be:
Atom counts:
O=1
Cl=4
N=6
S=3
Numeric
Nominal Molecule name: (1-methyl)(1,1,1-tributyl)azanium, tetrahexylammonium
Molecular surface:
Continuous
Phase state: solid, amorphous, liquid, gas, ionized
Categorical
Ordered Intestinal absorption: not absorbed, mildly absorbed, completely absorbed
Spectral domains:
Ranges
UV
visible
IR
EC 1. Oxidoreductases
Hierarchical EC numbers: EC 2. Transferases
EC 6.1 Forming Carbon-Oxygen Bonds
EC 3. Hydrolases
EC 4. Lyases
EC 5. Isomerases
EC 6. Ligases
EC 6.2 Forming Carbon-Sulfur Bonds
EC 6.3 Forming Carbon-Nitrogen Bonds
EC 6.4 Forming Carbon-Carbon Bonds
EC 6.5 Forming Phosphoric Ester Bonds
EC 6.6 Forming Nitrogen—Metal Bonds
Nature of learning
Unsupervised learning
Clustering
Rules
+
Supervised learning
Classification
Regression
Other
Reinforcement
First order logic
x, y xRy
Concept in data mining
A Concept is the target function to be learned
Concept is learned from
Instance 1
attributes-values
Relations
Sequences
Spatial
Instance 2
Instance 3
…
DB1
DB2
Machine Learning and Statistics
Data miner point of
view
Any hypothesis
compatible with the
dataset is useful
Search for all
hypothesis compatible
with the dataset
Induction
Statistician point of
view
Datasets are the
expression of
underlying probability
distributions
Datasets validate or
invalidate prior
hypothesis
Deduction
Validation in Data Mining
Validation means that a model is build on a
training set of data then applied on a test set of
data.
Success and failure on the test set must be
estimated.
The estimate is supposed to be representative of
any new situation.
Every model must be validated.
Training/Test
Split the dataset in two
parts:
One part is the training
set
The other is the test set
Bootstrapping
Draw N instances with
replacement from the
dataset
Create a training set
with these instances
Use the dataset as the
test set
Cross-Validation
Split the dataset in N
subsets
Use each subset as a
test set while all
others form a training
set
Scrambling
Reassign at random the
classes to the instances.
Success and failure are
estimated on the
scrambled data.
The goal is to estimate
good success
measurement by pure
chance.
Clustering
Search for an internal organization of the data
Optimizes relations between instances relative to
an objective function
Typical objective functions:
Separation
Coherence
Concept
Contiguity
Density
Cluster Evaluation
Essential because any dataset can be clustered by
not any cluster is meaningful.
Evaluation can
Unsupervised
Supervised
Relative
Unsupervised Cluster evaluation
Cohesion
Separation
Silhouette
Clustering Tendency
Proximity matrix
CoPhenetic Correlation
For p Nearest Neighbor Distances (NND) between
instances (ωi) and NND between rand points (ui)
Supervised cluster evaluation
Cluster3
Class1
Precision(3,1)
Recall(3,1)
Precision(i,j)
pij
Ni, number of members of cluster i
Recall(i,j)
Relative analysis
Compare two clustering.
Supervised cluster analysis is a special case of
relative analysis
The reference clustering is the set of classes
Rand statistics
Jaquard statistics
N00: number of instances couple in different clusters for both clustering
N11: number of instances couple in same clusters for both clusters
N01: number of instances couple in different clusters for the first clustering and in the same clusters for the second
N10: number of instances couple in the same clusters for the first clustering and in different one for the second.
A simple clustering algorithm: k-mean
1. Select k points as
centroids
2. Form k clusters: each
point is assigned to its
closest centroid
3. Reset each centroid to
the (geometric) center
of its cluster
4. Repeat from point 2
until no change is
observed
5. Repeat from point 1
until stable average
clusters are obtained.
X
X
XX
X
X
Classification
Definition
Assign one or several objects to predefined categories
The target function maps a set of attributes x to a set of
classes y.
Learning scheme
Supervised learning
Attribute-value
Goal
Predict the outcome of future observations
Probabilities basics
Conditional probabilities
Independence of random events:
Probability of realization of event A knowing that B has
occurred
The Bayes equation for independent events xi
Statistical approach to classification
Class2
Class 1
Estimate the probability of an instance {x1,x2}
being of Class1 or Class2.
The Naive Bayes assumption
The probability that an instance {x1,x2,…} belongs to class
A is difficult to estimate.
Poor statistics
Consider the Bayes Equation:
With the naive assumption that {x1,x2,…} are independent
Likelihood
Posterior Probability
Prior Probability
Evidence
The prior probability, the evidence and the likelihood
have better estimates
Good statistics
The Naive Bayes Classifier
1. Estimate the prior probability, P(A), for each
class.
2. Estimate the likelihood, P(x|A), of each attribute
for each class.
3. For a new instance, estimate the Bayes Score for
each class:
4. Assign the instance to the class which possesses
the highest score
•
The value of C can be optimized
Success and failure
For N instance and a give classifier, for each class I
NTP(i):
True Positives
• Number of instances of class i correctly classified.
NFP(i):
False Positives
• Number of instances incorrectly assigned to class i.
NTN(i):
True Negatives
• Number of instances of other classes correctly classified.
NFN(i):
False Negatives
• Number of instances of class i incorrectly assigned to other classes.
Confusion Matrix
For N instances, K classes
and a classifier
Nij, the number of
instances of class i
classified as j
Class1
Class2
… ClassK
Class1
N11
N12
… N1K
Class2
N21
N22
… N2K
…
…
…
… …
ClassK
NK1
NK2
… NKK
Classification Evaluation
Global measures of success
Measures are estimated on all classes
Local measures of success
Measures are estimated for each class
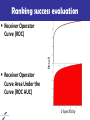
Ranking success evaluation
Recall
Receiver Operator
Curve (ROC)
Receiver Operator
Curve Area Under the
Curve (ROC AUC)
1-Specificity
Losses and Risks
Errors on a different class
prediction has different
costs
What does it cost to
mistakenly assign an
instance of one class to
another?
Normalized Expected Cost
Probability Cost Function
Cost matrix Cij
Class1
Class2
…
ClassK
Class1
0
C12
…
C1K
Class2
C21
0
…
C2K
…
…
…
…
…
ClassK
CK1
CK2
…
0
Asymmetric matrix
Cost Curve
Normalized expected cost
Worse classifier
NTP
Reject All Classifier
Accept All Classifier
Actual Classifier
NFP
Ideal Classifier
Probability Cost function
Conclusion
Data mining extracts useful information from
datasets
Clustering:
Unsupervised
Information about the data
Classification:
Supervised
Build models in order to predict outcome of future
observations
Multi-Linear Regression
y=ax+b
Sum of
Squared
Errors (SSE)
b
a