Download on Neutral Geometry II

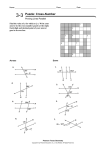
More on Neutral Geometry II (Including Sections 3.4 and 3.5)
Section 3.4: The Place of Parallels
Theorem 3.4.1 – The "Alternate Interior Angles (AIA)" Theorem
or also the "Congruent Alternate Interior Angles Make Parallel Lines" Theorem:
Two lines may or may not be parallel at first glance, but if at least one transversal of
the lines has congruent alternate interior angles, then the lines are indeed parallel.
(Pay attention to the way that the proof uses the Exterior Angle Theorem.)
Note: The Converse of the Alternate Interior Angle Theorem is NOT TRUE in Hyperbolic
Geometry, so the Converse cannot be proven in Neutral Geometry!
Corollary 3.4.2 - The "Common Perpendicular makes Parallel Lines" Theorem:
Two lines which are perpendicular to the same line are parallel lines.
Similar to the "Alternate Interior Angles" Theorem (Thm 3.4.1) are the following:
Corollary 3.4.3 - The "Congruent Corresponding Angles" Theorem.
If two lines have a transversal such that a pair of corresponding angles formed are
congruent, then the two lines must be parallel.
Corollary 3.4.4 - The "Supplementary Same-Side Interior Angles" Theorem:
If two lines have a transversal such that a pair of interior angles on the same side of the
transversal are supplementary, then the two lines must be parallel.
DEFINITION: The Euclidean Parallel Postulate (EPP):
For every line l and every point P not on line l , there is one and only one line m
that contains P and is parallel to l .
(This formulation of the EPP is sometimes called “Playfair’s Postulate.”)
Note: There are several theorems in Neutral Geometry which assert:
“The Euclidean Parallel Postulate is equivalent to ( ≡ ) Statement X,”
that is to say,
“The EPP is true if and only if Statement X is true. ”
2
To say that Statement X is equivalent to the Euclidean Parallel Postulate is also to say:
"Statement X can be proved true when the EPP is added as an axiom to those of
Neutral Geometry,
and
the EPP can be proved true when Statement X is added as an axiom to those of
Neutral Geometry."
The statement:
“The EPP is equivalent to Statement X.”
also means that,
if a model of Neutral Geometry is one for which the EPP is true, then Statement
X is also true for that model,
and
if a model of Neutral Geometry is one for which Statement X is true, then
the EPP is also true for that model,
For example, one such theorem of Neutral Geometry states:
“The EPP is equivalent to the statement “A rectangle exists.”
Once this has been proved, we will know that, if we add the statement “A rectangle exists”
to the list of SMSG Postulates 1 – 15, then we will be able to prove that the
Euclidean Parallel Postulate is true in the new axiom system and, therefore, the new
geometry we get by adding “A rectangle exists” as a postulate is Euclidean
Geometry.
It also means that, if we are considering a model of Neutral Geometry and we find that
a rectangle exists in that model, then we will know that the EPP is true in that model and,
therefore, that model of Neutral Geometry is also a model of Euclidean Geometry.
3
On the other hand, if we are considering a model of Neutral Geometry and we find that
rectangles do not exist in that model, then we will know that the EPP is false in that model
and (since the Elliptic Parallel Postulate is false in every model of Neutral Geometry)
therefore, we will know that the Hyperbolic Parallel Postulate is true in that model and
therefore, that model of Neutral Geometry is also a model of Hyperbolic Geometry.
When a statement has been proven to be equivalent to the EPP, then it will be a true
statement in Euclidean Geometry and it will be a false statement in Hyperbolic Geometry.
Some Statements Equivalent to the Euclidean Parallel Postulate (the EPP):
One statement equivalent to the EPP is Euclid's Fifth Postulate:
Theorem 3.4.5 - The "Euclid's 5th and EPP Equivalence" Theorem:
Euclid’s fifth postulate is equivalent to the Euclidean
Parallel Postulate.
The Converse Statement of the Alternate-Interior-Angles-Theorem is the following
statement:
When two lines are known to be parallel lines, then any transversal intersecting them
forms congruent alternate-interior angles.
The Converse of the AIA Theorem is FALSE in the Poincare Upper Half-plane model of
Hyperbolic Geometry, to the Converse of the AIA Theorem is FALSE in Hyperbolic
Geometry.
So, the Converse of the AIA Theorem cannot be proved using the axioms of Neutral
Geometry.
4
Other statements equivalent to the EPP are the following:
Theorem 3.4.6 - The "EPP and AIA Converse Equivalence" Theorem:
The EPP is equivalent to the Converse of the Alternate-Interior-Angle-Theorem .
Theorem 3.4.7 - The "EPP and 'Statement of Intersection' Equivalence" Theorem:
The EPP is equivalent to the following "statement of intersection":
“If a line intersects one of two parallel lines, then it intersects the other line.”
Theorem 3.4.8 - The "EPP and 'Statement of Perpendicularity' Equivalence" Theorem:
The EPP is equivalent to the following "statement of perpendicularity":
“If a line is perpendicular to one of two parallel lines,
then it is perpendicular to the other line.”
5
Section 3.5: The "Saccheri-Legendre" Theorem
or
The "Angle-Sum Less Than or Equal to 180 Degrees" Theorem
Definition:
A Saccheri Quadrilateral
:
a quadrilateral having two opposite congruent sides,
both perpendicular to a third side.
S
R
The BASE is this third side perpendicular to the two
sides. The right angles at the ends of the base are called
the BASE ANGLES. The side opposite the BASE is
P
Q
called the SUMMIT.
The angles at the ends of the summit are called the Summit Angles.
The following two lemmas are needed for use in proving the Saccheri-Legendre Theorem.
Lemma 3.5.2: The sum of the measures of any two angles in a triangle is
less than or equal to 180˚.
Lemma 3.5.3: For any triangle, ΔABC say, there exists a triangle, ΔA1B1C1 say,
such that ΔABC and ΔA1B1C1 have the same angle sum
and such that m (< A1) ≤ ½ m(< A) .
Theorem: 3.5.1 - The "Saccheri-Legendre" Theorem)
or
The "Angle-Sum Less Than or Equal to 180 Degrees" Theorem:
The angle sum of any triangle in Neutral Geometry is less than or equal to 180º.
Corollary: 3.5.4 -The "Angle-Sum Less Than or Equal to 360 Degrees" Theorem
The angle sum of any convex quadrilateral is less than or equal to 360.