Download Descriptive Statistics

Descriptive Statistics
The DESCRIPTIVE STATISTICS procedure displays univariate summary statistics for selected variables.
Descriptive statistics can be used to describe the basic features of the data in a study. It provides simple
summaries about the sample and the measures. Together with simple graphical analysis, it can form the
basis of quantitative data analysis.
How To
 Run STATISTICS->BASIC STATISTICS->DESCRIPTIVE STATISTICS.
 Select one or more variables.
 Optionally, use the PLOT HISTOGRAM option to build a histogram with frequencies and normal
curve overlay for each variable. Normal curve overlay is not available when a report is viewed in
Apple Numbers, because of a lack of combined charts support in the Numbers v3 app.
 By default, a table with descriptive statistics is produced for each variable. To view descriptive
statistics for all variables in a single table – select the “Single table” value for the Report option.
Report: For each variable
Report: Single table
In single table view the first column is
frozen, so you can scroll through the
report while the heading column stays
still.
 Optionally, select a method for computing percentiles. Percentiles are defined according to
Hyndman and Fan [HYN], see below for details.
Results
Table with summary statistics is produced for each variable. The table includes following statistics.
COUNT (𝑁) - sample size.
MEAN – arithmetic mean. The larger the sample size, the more reliable is its mean. The larger the
variation of data values, the less reliable the mean.
𝑁
1
𝑥̅ = ∑ 𝑥𝑖
𝑁
1
MEAN LCL, MEAN UCL – are the lower value (LCL) and upper value (UCL) of (1 − 𝛼)% reliable interval
limits estimate for the mean based on a t-distribution with 𝑁 − 1 degrees of freedom. The estimates are
made assuming that the population standard deviation is not known and that the variable is normally
distributed.
𝐿𝑜𝑤𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 = 𝑥̅ − 𝑡𝐶𝐿 𝑆𝑚
𝑈𝑝𝑝𝑒𝑟 𝑙𝑖𝑚𝑖𝑡 = 𝑥̅ − 𝑡𝐶𝐿 𝑆𝑚
𝑡𝐶𝐿 – t for the (1 − 𝛼)% confidence level (default value = 95%, default 𝛼 = 0.05). 𝛼 can be changed in
the PREFERENCES.
𝑆𝑚 – estimated standard error of the mean.
LCL is for Lower Confidence Limit and UCL is for Upper Confidence Limit.
VARIANCE (UNBIASED ESTIMATE ) - is the mean value of the square of the deviation of that variable from its
mean with Bessel's correction.
𝑁
1
𝑠 =
∑(𝑥𝑖 − 𝑥̅ )2
𝑁−1
2
1
Population variance is estimated as
𝑁
1
𝜎 = ∑(𝑥𝑖 − 𝑥̅ )2 = 𝜇2 ,
𝑁
2
1
where 𝜇2 is second moment (see below).
STANDARD DEVIATION - square root of the variance.
𝑁
1
𝜎 = √ ∑(𝑥𝑖 − 𝑥̅ )2
𝑁
1
STANDARD ERROR (OF MEAN) - quantifies the precision of the mean. It is a measure of how far your
sample mean is likely to be from the true population mean. The formula shows that the larger the
sample size, the smaller the standard error of the mean. More specifically, the size of the standard error
of the mean is inversely proportional to the square root of the sample size.
𝑆𝐸𝑀 =
𝜎
√𝑁
MINIMUM – the smallest value for a variable.
MAXIMUM – the largest value for a variable.
RANGE - difference between the largest and smallest values of a variable. For normally distributed
variable dividing the range by six can make a quick estimate of the standard deviation.
SUM – sum of the sample values.
SUM STANDARD E RROR - standard deviation of sums distribution.
TOTAL SUM SQUARES - the sum of the squared values of the variable. Sometimes referred to as the
unadjusted sum of squares.
𝑁
𝑇𝑆𝑆 = ∑ 𝑥𝑖 2
1
ADJUSTED SUM SQUARES - the sum of the squared differences from the mean.
𝑁
𝐴𝑑𝑗𝑆𝑆 = ∑(𝑥𝑖 − 𝑥̅ )2
1
GEOMETRIC MEAN - a type of mean, which indicates the central tendency of a set of numbers. It is similar
to the arithmetic mean, except that instead of adding observations and then dividing the sum by the
count of observations, n, the observations are multiplied, and then the nth root of the resulting product
is taken.
𝑁
𝑁
𝐺 = √∏ 𝑥𝑖
1
HARMONIC MEAN - the number 𝐻 defined by
𝑁
1
1
𝐻= ∑
𝑁
𝑥𝑖
1
MODE - the value that occurs most frequently in the sample. The mode is a measure of central tendency.
It is not necessarily unique since the same maximum frequency may be attained at different values (in
this case #N/A is displayed).
SKEWNESS – a measure of the asymmetry of the variable. A value of zero indicates a symmetrical
distribution, i.e. Mean = Median. The typical definition is:
𝑁
𝑁
1
1
𝜇3
1
𝑥𝑖 − 𝑥̅ 3
𝛾1 = ∑ 3/2 = ∑(
)
𝑁
𝜎
𝜎
There are different formulas for estimating skewness and kurtosis [JOA]. The formula above is used in
many textbooks and some software packages (NCSS, Wolfram Mathematica). Use the SKEWNESS
(FISHER'S) value to get the same results as in SPSS, SAS and Excel software.
SKEWNESS STANDARD ERROR – large sample estimate of the standard error of skewness for an infinite
population.
𝑘1 =
𝛾1
𝜎3
KURTOSIS - a measure of the "peakedness" of the variable. Higher kurtosis means more of the variance is
the result of infrequent extreme deviations, as opposed to frequent modestly sized deviations. If the
kurtosis equals three and the skewness is zero, the distribution is normal.
𝑁
𝑁
1
1
𝜇4 1
𝑥𝑖 − 𝑥̅ 4
𝛾2 = ∑ 2 = ∑ (
)
𝜎
𝑁
𝜎
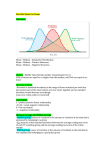
If 𝛾2 = 3 – the distribution is mesokurtic.
If 𝛾2 > 3 – the distribution is leptokurtic.
If 𝛾2 < 3 – the distribution is platykurtic.
𝛾2 = 3
𝛾2 > 3
𝛾2 < 3
Biased estimate for kurtosis is
𝑁
𝑁
1
1
𝜇4
1
𝑥𝑖 − 𝑥̅ 4
𝛾2 = ∑ 2 − 3 = ∑ (
) −3
𝜎
𝑁
𝜎
There are different formulas for estimating skewness and kurtosis [JOA]. The formula above is used in
many textbooks and some software packages (NCSS, Wolfram Mathematica). Use the KURTOSIS
(FISHER'S) value to get the same results with SPSS, SAS and Excel software.
KURTOSIS STANDARD ERROR - large sample estimate of the standard error of kurtosis for an infinite
population.
𝑛2 − 1
𝑘2 = 2𝑘1 √
(𝑛 − 3)(𝑛 + 5)
SKEWNESS (FISHER 'S) – a bias-corrected measure of skewness. Also known as FISHER'S SKEWNESS G 1.
𝑔1 =
√𝑛(𝑛 − 1)
𝛾1
𝑛−2
KURTOSIS (FISHER'S)- an alternative measure of kurtosis based on the unbiased estimators of moments.
Also known as FISHER'S KURTOSIS G2.
𝑔2 =
(𝑛 + 1)(𝑛 − 1)
𝑛−1
{𝛾2 − 3
}
(𝑛 − 2)(𝑛 − 3)
𝑛+1
COEFFICIENT OF VARIATION - a normalized measure of dispersion of a probability distribution. Defined only
for non-zero mean, and is most useful for variables that are always positive. It is also known as unitized
risk or the variation coefficient.
𝜎
𝑐𝑣 =
𝑥̅
MEAN DEVIATION (MEAN ABSOLUTE DEVIATION, MD) - mean of the absolute deviations of a set of data
about the data's mean.
𝑁
1
𝑀𝐷 = ∑ |𝑥𝑖 − 𝑥̅ |
𝑁
1
SECOND MOMENT, THIRD MOMENT, FOURTH MOMENT – raw moments about zero. A jth raw moment about
zero is defined as
𝑁
1
𝜇𝑗 = ∑(𝑥𝑖 − 𝑥̅ )𝑗
𝑁
1
Second moment 𝜇2 is biased variance estimate.
MEDIAN - the observation that splits the variable into two halves. The median of a sample can be found
by arranging all the sample values from lowest value to highest value and picking the middle one.
MEDIAN E RROR - the number defined by
𝜋
𝑆𝐸𝑀 = 𝑠√
2𝑁
PERCENTILE 25% (Q1) - value of a variable below which 25% percent of observations fall.
PERCENTILE 75% (Q2) - value of a variable below which 75% percent of observations fall.
PERCENTILE DEFINITION
You can change the percentile calculation method in the ADVANCED OPTIONS. Nine methods from
Hyndman and Fan [HYN] are implemented. Sample quantiles are based on one or two order statistics
and can be written as 𝑄(𝑝) = (1 − 𝛾) 𝑋(𝑗) + 𝛾 𝑋(𝑗+1), where 𝑋(𝑗) is the sample order statistics and 𝛾
(0 ≤ 𝛾 ≤ 1) is a real-valued function of 𝑗 = ⌊𝑝𝑁 + 𝑚⌋ (largest integer not greater than 𝑝𝑛 + 𝑚) and
𝑔 = frac(𝑝𝑛 + 𝑚), m – real constant.
Discontinuous definitions
1. Inverse of EDF (SAS-3)
The oldest and most studied definition that uses
the inverse of the empirical distribution function
(EDF).
𝛾 = 1 𝑖𝑓 𝑔 > 0
{
, 𝑔 = 𝑁𝑝 (𝑚 = 0)
𝛾 = 0 𝑖𝑓 𝑔 = 0
2. EDF with averaging (SAS-5)
Similar to the previous definition, but averaging is
used when 𝑔 = 0.
𝛾 = 1 𝑖𝑓 𝑔 > 0
{
, 𝑔 = 𝑁𝑝 (𝑚 = 0)
𝛾 = 1/2 𝑖𝑓 𝑔 = 0
3. Observation closest to N*p (SAS-2)
Defined as the order statistic 𝑋(𝑘) , where k is the
nearest integer to 𝑁𝑝.
Continuous definitions
4. Interpolation of EDF (SAS-1)
Defined as the linear interpolation of function from
the first definition, 𝑝𝑘 = 𝑘/𝑁.
5. Piecewise linear interpolation of EDF
(midway values as knots)
Piecewise linear function with knots defined as
values midway through the steps of the EDF,
𝑝𝑘 = (𝑘 − 0.5)/𝑁.
6. Interpolation of the expectations for
the order statistics (SPSS, NIST)
Knots are defined as the order statistics
expectations. In definitions 6 – 8, 𝐹[𝑋(𝑘) ] has the
th
distribution of the k order statistics from a
uniform distribution, namely the 𝛽(𝑘, 𝑁 − 𝑘 + 1).
This definition is used by Minitab* and SPSS*
packages.
𝑝𝑘 = E 𝐹[𝑋(𝑘) ] = 𝑘 /(𝑁 + 1).
7. Interpolation of the modes for the
order statistics (Excel)
Linear interpolation of the order statistics modes.
8. Interpolation of the approximate
medians for order statistics
Linear interpolation of the order statistics medians.
Median position M 𝐹[𝑋(𝑘) ] is approximated as
M 𝐹[𝑋(𝑘) ] ≈ (𝑘 − 1⁄3) /(𝑁 + 1⁄3).
𝐹[𝑋(𝑘) ] is defined the same way as in (6).
𝑝𝑘 = mode 𝐹[𝑋(𝑘) ] = (𝑘 − 1) /(𝑁 − 1).
𝑝𝑘 = (𝑘 − 1⁄3) /(𝑁 + 1⁄3).
9. Blom's unbiased approximation
This definition, proposed by Blom (1958), is an
approximately unbiased approximation of 𝑄(𝑝)
when 𝐹 is normal.
𝑝𝑘 = (𝑘 − 3⁄8) /(𝑁 + 1⁄4).
IQR (INTERQUARTILE RANGE , MIDSPREAD) – the difference between the third quartile and the first quartile
(between the 75th percentile and the 25th percentile). IQR represents the range of the middle 50
percent of the distribution. It is a very robust (not affected by outliers) measure of dispersion. The IQR is
used to build box plots.
𝐼𝑄𝑅 = 𝑄3 − 𝑄1
MAD (MEDIAN ABSOLUTE D EVIATION) - a robust measure of the variability of a univariate sample of
quantitative data. The median absolute deviation is a measure of statistical dispersion. It is a more
robust estimator of scale than the sample variance or standard deviation.
𝑀𝐴𝐷 = 𝑚𝑒𝑑𝑖𝑎𝑛𝑖 {|𝑥𝑖 − 𝑚𝑒𝑑𝑖𝑎𝑛𝑗 (𝑥𝑗 )|}
COEFFICIENT OF DISPERSION – a measure of relative inequality (or relative variation) of the data.
COEFFICIENT OF DISPERSION is the ratio of the Average Absolute Deviation from the Median (MAAD) to the
Median of the data.
𝐶𝐷 =
1 𝑀𝐴𝐷
|
|
𝑁 𝑀𝑒𝑑𝑖𝑎𝑛
Histogram for each variable is plotted when checked in the ADVANCED OPTIONS. If you want to specify
bins manually – consider using the STATISTICS->BASIC STATISTICS ->HISTOGRAM command.
References
[HYN] Hyndman, R.J. and Fan, Y. (November 1996). "Sample Quantiles in Statistical Packages", The
American Statistician 50 (4): pp. 361–365.
[JOA] D. N. Joanes and C. A. Gill (1998), Comparing measures of sample skewness and kurtosis. The
Statistician, 47, 183–189.