Download AHEART August 46/2 - AJP

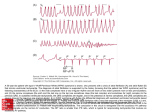
Ventricular response in atrial fibrillation:
random or deterministic?
KENNETH M. STEIN,1 JEFF WALDEN,1 NEAL LIPPMAN,2 AND BRUCE B. LERMAN1
of Cardiology, Department of Medicine, New York Hospital-Cornell Medical Center,
New York, New York 10021; and 2Division of Cardiology, Department of Medicine,
University of Connecticut, Farmington, Connecticut 06030
1Division
heart rate; nonlinear dynamics
random system is equally unpredictable in both short
and long terms.
Techniques of nonlinear dynamics have been applied
to the analysis of heart rate variability during sinus
rhythm. Although the issue of whether sinus rhythm is
chaotic remains controversial (16), these techniques
have been used successfully for risk stratification (18,
19). In contrast, although the irregular ventricular
intervals in atrial fibrillation are often described as
chaotic, it has yet to be shown that this represents
chaos in the mathematical sense. Thus, although reduced heart rate variability during atrial fibrillation
conveys an increased cardiovascular risk (20), the
underlying dynamics of the ventricular response during atrial fibrillation are incompletely understood.
To better understand whether the ventricular response in atrial fibrillation is chaotic, we developed an
algorithm [based on an original proposal by Sugihara
and May (25)] that uses nonlinear predictive forecasting to search for evidence of sensitive dependence on
initial conditions in a time series. We applied the
algorithm to a set of simulated R-R intervals (‘‘test
sets’’) and to the analysis of R-R interval sequences
obtained in 16 patients during chronic atrial fibrillation. A similar algorithm previously has been demonstrated to be useful for interpolating to correct for the
effects of ectopy in calculations of heart rate variability
during sinus rhythm (9, 10).
METHODS
CHAOS THEORY, referring to the overlapping mathematical disciplines of fractal geometry and nonlinear dynamics, has been used to provide insight into the pathophysiology and prognostic importance of cardiac arrhythmias
(2–5, 8, 22, 23). In the mathematical sense, ‘‘chaos’’
refers to a system that is aperiodic but deterministic
(nonrandom). A defining characteristic of chaotic behavior is sensitive dependence on initial conditions; i.e.,
similar sequences evolve similarly in the near future
but then diverge exponentially. Because of sensitive
dependence on initial conditions, if the dynamics of a
chaotic system are sufficiently described, the behavior
of the system can be predicted in the short term but,
due to inherent imprecision in measurement, not in the
long term. In contrast, a linear system is equally
predictable in both short and long terms, whereas a
The costs of publication of this article were defrayed in part by the
payment of page charges. The article must therefore be hereby
marked ‘‘advertisement’’ in accordance with 18 U.S.C. Section 1734
solely to indicate this fact.
H452
Nonlinear predictive forecasting. The behavior of every
nonrandom (deterministic) system, no matter how complex,
can be considered to occur within a ‘‘phase space,’’ which can
be represented by a Cartesian coordinate system with one
axis for each of the variables necessary to completely describe
the state of the system at any given time. For most biologic
systems, the nature of these variables, or even their number,
is unknown. However, a topological equivalent of phase space
can be constructed from empirical data using the technique of
‘‘lags’’ (26). With the use of this technique, an embedding
dimension (E) is chosen and the points that constitute a
phase space are represented as the vectors
X n ⫽ (RRn, RRn⫺L, RRn⫺2L, . . . , RRn⫺(E⫺1)L)
(1)
where RRn is the nth R-R interval in the time series and L, the
lag, is a positive integer. As proposed by Sugihara and May
(25), the future behavior of a system may be predicted
(‘‘forecasted’’) by observing other sufficiently similar trajectories in phase space. Importantly, and in distinction from other
methods of forecasting such as autoregressive modeling, this
scheme does not require any assumptions about the underlying mathematical relationships of the system other than the
initial assumption that the system is deterministic (or, more
0363-6135/99 $5.00 Copyright r 1999 the American Physiological Society
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
Stein, Kenneth M., Jeff Walden, Neal Lippman, and
Bruce B. Lerman. Ventricular response in atrial fibrillation:
random or deterministic? Am. J. Physiol. 277 (Heart Circ.
Physiol. 46): H452–H458, 1999.—The ventricular response in
atrial fibrillation is often described as ‘‘chaotic,’’ but this has
not been demonstrated in the strict mathematical sense. A
defining feature of chaotic systems is sensitive dependence on
initial conditions: similar sequences evolve similarly in the
short term but then diverge exponentially. We developed a
nonlinear predictive forecasting algorithm to search for predictability and sensitive dependence on initial conditions in
the ventricular response during atrial fibrillation. The algorithm was tested for simulated R-R intervals from a linear
oscillator with and without superimposed white noise, a
chaotic signal (the logistic map) with and without superimposed white noise, and a pseudorandom signal and was then
applied to R-R intervals from 16 chronic atrial fibrillation
patients. Short-term predictability was demonstrated for the
linear oscillators, without loss of predictive ability farther
into the future. The chaotic system demonstrated high shortterm predictability that declined rapidly further into the
future. The pseudorandom signal was unpredictable. The
ventricular response in atrial fibrillation was weakly predictable (statistically significant predictability in 8 of 16 patients), without sensitive dependence on initial conditions.
Although the R-R interval sequence is not completely unpredictable, a low-dimensional chaotic attractor does not govern
the irregular ventricular response during atrial fibrillation.
H453
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
冑
X(t) ⫽ 800 ⫹ 100 sin
1 25 2 ⫹ 100 sin 1 5 2
2␲t
2␲t
2) A linear oscillator with a high signal-to-noise ratio was
constructed [using a computerized pseudorandom number
(Rand) generator]
X(t) ⫽ 800 ⫹ 100 sin
1 25 2 ⫹ 100 sin 1 5 2 ⫹ Rand(⫺25, ⫹25)
2␲t
2␲t
3) A linear oscillator with a low signal-to-noise ratio was
constructed
X(t) ⫽ 800 ⫹ 50 sin
1 25 2 ⫹ 50 sin 1 5 2 ⫹ Rand (⫺100, ⫹100)
2␲t
2␲t
4) A chaotic system was constructed using the logistic map, a
known chaotic system. This system is iteratively determined
according to the equations
Y(t) ⫽ ␭(Yt⫺1)(1 ⫺ Yt⫺1)
␭⫽4
X(t) ⫽ 600 ⫹ 400Y(t)
5) A chaotic system with a high signal-to-noise ratio was
constructed by adding uniformly random numbers scaled
over the interval (⫺25, ⫹25) to the values X(t) from the
logistic map in test set 4. 6) A chaotic system with a low
signal-to-noise ratio was constructed by adding uniformly
random numbers scaled over the interval (⫺100, ⫹100) to the
values X(t) from the logistic map. 7) Finally, a random system
consisting of uniformly random numbers scaled over the
interval (600, 1,000) was constructed.
Atrial fibrillation. In 16 patients with chronic atrial fibrillation, 24-h ambulatory electrocardiographic recordings of bipolar leads CM1 and CM5 were obtained using a standard
reel-to-reel Holter monitoring system (Del Mar Avionics,
Irvine, CA) and scanned by a computer-based system (Marquette Laser XP; Marquette Electronics, Milwaukee, WI)
with total visual verification and correction of beat morphology and timing by one of the authors. The results were
digitized at 128 Hz, yielding an approximate temporal resolution of 8 ms. After scanning was completed, the first series of
ⱕ2,000 consecutive R-R intervals without intervening ventricular ectopic beats or artifact was extracted for each
patient and downloaded to a personal computer for application of the identical algorithm used for the test sets.
Statistical and power spectral analysis. The significance of
the observed Pearson correlation coefficients was determined
using a standard two-tailed t-test. A P value ⬍0.01 was taken
as indicating that a correlation was significantly different
from zero (i.e., was significantly predictable). For data sets of
1,600–2,000 beats this criterion for weak but significant
predictability approximately corresponds to a correlation
coefficient ⬎0.06. Grouped comparisons of continuous variables were made via the t-test. Grouped comparisons of
dichotomous variables were made via Fisher’s exact test. For
these purposes a P value ⬍0.05 was required to reject the null
hypothesis. Power spectra were computed for raw heart
period data using a 1,024-point fast Fourier transform algorithm with a Tukey-Hamming window (11 point).
RESULTS
Test sets. As long as a minimum of 100 intervals was
specified, short-term predictability was demonstrated
for the system of linear oscillators with no loss of
predictive ability farther into the future even in the
presence of a large amount of noise (low signal-to-noise
ratio) (Fig. 1). For the case of 50 points, short-term
predictability was paradoxically improved by the addition of noise; this may relate to boundary and/or
aliasing effects specific to sampling 50 points of the
function sin (2␲t/25) ⫹ sin (2␲t/5). In contrast, although the chaotic system demonstrated high shortterm predictability, the correlation between predicted
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
precisely, that its behavior can be described within a phase
space of finite dimension).
The nonlinear predictive forecasting algorithm therefore
consists of the following steps. 1) The technique of lags is used
to reconstruct 8 different phase spaces with embedding
dimensions from 3 to 10. 2) For each R-R interval in the time
series (RRi ), the three nearest neighbors in each phase space,
determined using the Cartesian distance metric ⑀i,j ⫽
(Xi⫺Xj)2 are chosen from every other point (RRj ) in the same
time series. The predicted next R-R interval (RRi⫹1 ) is
determined as the average of the R-R intervals that follow
(RRj⫹1 ) the three nearest neighbors (each weighted by the
inverse of its ⑀i,j ). 3) The Pearson correlation coefficient (r)
between predicted and actual R-R intervals is computed
for all intervals in the time series for each of the eight phase
spaces. 4) The phase space with the embedding dimension
yielding the highest correlation coefficient is determined.
Within that embedding dimension, the 3 nearest neighbors
of each R-R interval trajectory in phase space are used to
predict the evolution of that trajectory from 1 to 10 steps
into the future using a method analogous to that described
in the second step. For a system of dimension n, and for a
sufficiently large data set, the correlation coefficient should
be approximately the same for all embedding dimensions
⬎n. Therefore, the embedding dimension giving the maximum correlation coefficient does not strictly correspond to
the dimension of the system but suffices for the practical
purpose of nonlinear prediction. 5) For each distance into the
future, the correlation coefficient between predicted and
actual R-R intervals is computed for all intervals in the time
series.
The algorithm can be used to test for the hallmark of
chaotic systems: sensitive dependence on initial conditions.
In linear systems, nearby trajectories tend to remain nearby,
and therefore these systems are equally predictable in the far
future as well as in the near future. Random sequences, in
contrast, are equally unpredictable in both the near future
and far future. In chaotic systems, however, nearby trajectories tend to diverge exponentially. Therefore, they are predictable in the near future but not the far future. For example,
the weather is easily predictable 5 min into the future,
modestly predictable 5 h into the future, and virtually
unpredictable 5 days into the future. By computing the
(Pearson) correlations between values predicted from 1 to 10
steps into the future using the nonlinear predictive forecasting algorithm, we can therefore gain insight into whether the
system behaves more like a linear system, a random system,
or a chaotic system.
Simulated R-R intervals. We tested the above algorithm by
applying it to computer-generated sequences of simulated
R-R intervals (test sets) of varying lengths (50–2,000 intervals) and with varying amounts of added noise to assess the
impact of sequence length and measurement error on the
performance of the algorithm. The following test sets were
created. 1) A linear oscillator was constructed (chosen to
simulate the dominant low- and high-frequency oscillations
in human heart period during sinus rhythm)
H454
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
and actual intervals declined rapidly with attempts to
forecast further into the future. The chaotic signal was
distinctive with as few as 50 intervals to analyze in the
presence of a high signal-to-noise ratio, although not in
the presence of a low signal-to-noise ratio (Fig. 2). As
expected, the pseudorandom signal was not predictable.
Atrial fibrillation. The group of 16 patients with
chronic atrial fibrillation included 9 males and 7 females with a mean age of 57 ⫾ 12 yr. Of the 16 patients,
6 had no underlying cardiovascular disease, 5 had
significant valvular heart disease (mitral regurgitation
or mixed rheumatic valvular disease), 1 had an ischemic cardiomyopathy, and 3 had hypertension. Two
Fig. 1. Correlations between observed and predicted values at varying distances into the future as a function of sample size. Results are
shown for a system of sinusoidal oscillators (Sin) and for sinusoidal
systems with a low (LN) or high (HN) amount of superimposed
random noise. Although predictability was less for the HN system
than other systems, as long as the sample contained ⱖ100 observations, dynamics were somewhat predictable for all systems and
predictability did not deteriorate for increasing distances into the
future. N, no. of observations.
patients had mitral valve prolapse without significant
mitral regurgitation (including 1 patient with coexisting hypertension). Also, 12 of 15 patients were being
treated with digoxin, 4 of 15 were on ␤-blockers, 3 of 15
were on calcium-channel blockers, and 4 of 15 were on
antiarrhythmic drug therapy (2 on procainamide, 1 on
amiodarone, and 1 on propafenone). One patient’s
medications could not be ascertained with certainty. No
patient had clinical evidence of digitalis intoxication.
During the recording period, the mean R-R interval
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
Fig. 2. Correlations between observed and predicted values at varying distances into the future as a function of sample size. Results are
shown for the logistic map (Log; evaluated in its chaotic domain), for
Log with a low amount of superimposed random noise (Log ⫹ LN),
and for Log with a high amount of superimposed random noise (Log ⫹
HN). For logistic maps, as long as the sample contained ⱖ100
observations, dynamics were predictable in short term (future ⫽ 1),
but predictability deteriorated significantly with increasing distances into the future.
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
was 804 ⫾ 186 ms (range: 539–1,090 ms). The average
standard deviation of the R-R interval was 178 ⫾ 48 ms
(range: 118–254 ms). In contrast, for the uniform
random signal tested, the mean was 797 and the
standard deviation was 143.
The best embedding dimension for prediction one
beat into the future (future ⫽ 1) ranged from 3 to 10
(mean: 5.9 ⫾ 2.7). As shown in Fig. 3 there was no
characteristic best embedding dimension for the group
as a whole. With the use of each individual patient’s
best embedding dimension, the ventricular response in
atrial fibrillation was only weakly predictable at all
time scales and there was no evidence of sensitive
dependence on initial conditions (Fig. 4).
However, in 8 of 16 patients, the R-R interval series
was significantly (albeit weakly) predictable as evidenced by a correlation coefficient significantly different from zero (Fig. 5). These patients were not signifi-
Fig. 4. Correlations (means ⫾ SE) between observed and predicted
values at varying distances into the future for patients with atrial
fibrillation using each patient’s individual optimal embedding dimension. Ventricular response was only weakly predictable at all time
scales, and there was no deterioration of predictability with increasing distance into the future.
Fig. 5. Individual data showing correlations between observed and
predicted values at varying distances into the future for patients with
atrial fibrillation using each patient’s individual optimal embedding
dimension. For a subset of patients, ventricular response was significantly (albeit modestly) predictable without deterioration at increasing distances into the future.
cantly different from their counterparts in age, gender,
presence of structural heart disease, medications, mean
R-R interval, standard deviation of the R-R interval,
number of beats analyzed, or best embedding dimension (all P ⬎ 0.10). For two individual patients, the
ventricular response was moderately predictable (r
values of 0.37 and 0.56, respectively, at future ⫽ 1) but
did not show evidence of sensitive dependence on initial
conditions. Although the significance is uncertain, electrocardiograms (ECG) from these patients demonstrated notably ‘‘coarse’’ fibrillatory activity (Fig. 6).
Power spectral analysis revealed broad-band power
spectra for all patients. The power spectrum for the
patient with the highest degree of nonlinear predictability is shown in Fig. 7.
DISCUSSION
The principal findings of the present study are 1)
that a nonlinear forecasting algorithm can feasibly be
applied to R-R interval data sets and, as evidenced by
the performance when applied to computer-generated
test sets, can reliably discriminate linear, chaotic, and
random types of behavior; 2) that the ventricular
response in atrial fibrillation does not appear to represent chaos in the strict mathematical sense of a deterministic aperiodic system; and 3) that, in a significant
number of patients, the beat-to-beat ventricular response in atrial fibrillation is not wholly unpredictable.
Nonlinear forecasting. The results in the test sets
demonstrate that nonlinear forecasting is a practical
approach for qualitatively analyzing the dynamics of a
complex system such as that generating the R-R interval data stream. Nonlinear forecasting was initially
proposed by Sugihara and May (25) for application to
biologic time-series data. The primary advantage of
this approach versus linear forecasting systems (e.g.,
power spectral analysis or autoregressive modeling) is
that it does not require any assumptions about the
underlying mathematics of the system beyond the
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
Fig. 3. Correlations (means ⫾ SE) between observed and predicted
values in short term (future ⫽ 1) as a function of embedding
dimension for patients with atrial fibrillation. There is no characteristic ‘‘best’’ embedding dimension and no suggestion that prediction is
improved at higher dimensions.
H455
H456
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
hypothesis that the system is deterministic (i.e., predictable).
Other methods that can be used to look for evidence
of chaotic behavior include estimation of the dimension
of the attractor for the system to be analyzed (a
measure of complexity/aperiodicity) (8) and estimation
of the largest Lyapunov exponent of the system (a
measure of sensitive dependence on initial conditions).
In theory, nonlinear forecasting has an advantage over
the former approach in that it is less dependent on very
long data streams for accurate interpretation (27) and
an advantage over the latter approach in that it is more
Fig. 7. Power spectral analysis of heart period data from the patient
whose ventricular response demonstrated the greatest degree of
predictability. Spectrum is ‘‘broad band,’’ with no discrete highfrequency peaks.
robust and less dependent on initial assumptions about
the behavior of the system.
Predictability of atrial fibrillation. This is the first
analysis to discover evidence of significant (although
weak) predictability in the beat-to-beat changes in the
ventricular response in atrial fibrillation in some patients. Subtle ordering has previously been demonstrated in atrial activation during atrial fibrillation (7,
17). Significant positive or negative correlations between successive ventricular beats during atrial fibrillation have been described in some human subjects (15)
as well as in some animal models (14). However, most
analyses have not demonstrated any systematic order
to the ventricular response during atrial fibrillation in
humans, and most authorities describe the pulse in
atrial fibrillation as random (1, 6, 12, 29). It is possible
that these results differed from ours because the analytic approach (autoregression) depends on an assumption of strict linearity. The signals that we observed
were most compatible with a weak linear system
superimposed on a very noisy background (cf. Figs. 1
and 4). There was no evidence of sensitive dependence
on initial conditions, and our results are therefore not
compatible with the notion that the ventricular response in atrial fibrillation might represent a form of
low-dimensional chaos.
Although the present analysis shows weak predictability in the ventricular response during atrial fibrillation, it does not permit us to identify the physiological
causes of that predictability in these patients. However,
van den Berg and colleagues (28) have previously
demonstrated a moderate correlation between heart
rate variability in atrial fibrillation and systemic vagal
tone. These observations might explain the analogy
between the prognostic utility of measures of heart rate
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
Fig. 6. A 12-lead electrocardiogram from the patient whose ventricular response demonstrated the greatest degree
of predictability. Notably ‘‘coarse’’ fibrillatory activity is present.
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
Address for reprint requests and other correspondence: K. M.
Stein, Div. of Cardiology, Starr-4, New York Hospital-Cornell Medical
Center, 525 East 68th St., New York, NY 10021 (E-mail: kstein@
mail.med.cornell.edu).
Received 1 September 1998; accepted in final form 12 March 1999.
REFERENCES
1. Bootsma, B. K., A. J. Hoelen, J. Strackee, and F. L. Meijler.
Analysis of R-R intervals in patients with atrial fibrillation at
rest and during exercise. Circulation 61: 783–794, 1970.
2. Denton, T. M., G. A. Diamond, R. H. Helfant, S. Khan, and
H. Karaguezian. Fascinating rhythm: a primer on chaos theory
and its application to cardiology. Am. Heart J. 120: 1419–1440,
1990.
3. Garfinkel, A., M. L. Spano, W. L. Ditto, and J. N. Weiss.
Controlling cardiac chaos. Science 257: 1230–1235, 1992.
4. Glass, L. Complex cardiac rhythms. Nature 330: 695–696, 1987.
5. Goldberger, A. L., L. J. Findley, M. R. Blackburn, and A. J.
Mandell. Nonlinear dynamics in heart failure: implications of
long-wavelength cardiopulmonary oscillations. Am. Heart J. 107:
612–615, 1984.
6. Hayano, J., F. Yamasaki, S. Sakata, A. Okada, S. Mukai, and
T. Fujinami. Spectral characteristics of ventricular response to
atrial fibrillation. Am. J. Physiol. 273 (Heart Circ. Physiol. 42):
H2811–H2816, 1997.
7. Hoekstra, B. P. T., M. A. Allessie, and J. DeGoede. Nonlinear
analysis of epicardial atrial electrograms of electrically induced
atrial fibrillation in man. J. Cardiovasc. Electrophysiol. 6: 419–
440, 1995.
8. Kaplan, D. T., and R. J. Cohen. Is fibrillation chaos? Circ. Res.
67: 886–892, 1990.
9. Lippman, N., K. M. Stein, and B. B. Lerman. Nonlinear
predictive interpolation. A new method for the correction of
ectopic beats for heart rate variability analysis. J. Electrocardiol.
26, Suppl.: S14–S19, 1993.
10. Lippman, N., K. M. Stein, and B. B. Lerman. Comparison of
methods for removal of ectopy in measurement of heart rate
variability. Am. J. Physiol. 267 (Heart Circ. Physiol. 36): H411–
H418, 1994.
11. Markowitz, S. M., K. M. Stein, and B. B. Lerman. Mechanism
of rate control following radiofrequency modification of atrioventricular conduction in patients with atrial fibrillation. Circulation 94: 2856–2864, 1996.
12. Meijler, F. L. The pulse in atrial fibrillation. Br. Heart J. 56: 1–3,
1986.
13. Meijler, F. L., J. Jalife, J. Beaumont, and D. Vaidya. AV
nodal function during atrial fibrillation: the role of electrotonic
modulation of propagation. J. Cardiovasc. Electrophysiol. 7:
843–861, 1996.
14. Meijler, F. L., J. Kroneman, I. van der Tweel, J. N. Herbschleb, R. M. Heethaar, and C. Borst. Nonrandom ventricular
rhythm in horses with atrial fibrillation and its significance for
patients. J. Am. Coll. Cardiol. 4: 316–323, 1984.
15. Rawles, J. M., and E. Rowland. Is the pulse in atrial fibrillation irregularly irregular? Br. Heart J. 56: 4–11, 1986.
16. Roach, D. E., and R. S. Sheldon. Information scaling properties of heart rate variability. Am. J. Physiol. 274 (Heart Circ.
Physiol. 43): H1970–H1978, 1998.
17. Schoenwald, A. T., A. V. Sahakian, H. J. Sih, and S. Swiryn.
Further observations of ‘‘linking’’ of atrial excitation during
clinical atrial fibrillation. Pacing Clin. Electrophysiol. 21: 25–34,
1998.
18. Skinner, J. E., C. Carpeggiani, C. E. Landsman, and K. W.
Fulton. Correlation dimension of heartbeat intervals is reduced
in conscious pigs by myocardial ischemia. Circ. Res. 68: 966–976,
1991.
19. Skinner, J. E., C. M. Pratt, and T. Vybiral. A reduction in the
correlation dimension of heartbeat intervals precedes imminent
ventricular fibrillation in human subjects. Am. Heart J. 125:
731–743, 1993.
20. Stein, K. M., J. S. Borer, C. Hochreiter, R. B. Devereux, and
P. Kligfield. Variability of the ventricular response in atrial
fibrillation and prognosis in chronic nonischemic mitral regurgitation. Am. J. Cardiol. 74: 906–911, 1994.
21. Stein, K. M., J. S. Borer, C. Hochreiter, P. M. Okin, E. M.
Herrold, R. B. Devereux, and P. Kligfield. Prognostic value
and physiologic correlates of heart rate variability in chronic
severe mitral regurgitation. Circulation 88: 127–135, 1993.
22. Stein, K. M., L. A. Karagounis, J. L. Anderson, P. Kligfield,
and B. B. Lerman. Fractal clustering of ventricular ectopy
correlates with sympathetic tone preceding ectopic beats. Circulation 91: 722–727, 1995.
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017
variability in atrial fibrillation and the same measures
in sinus rhythm (20, 21). It is possible that the weak
predictability demonstrated in the present study represents the effect of cyclic oscillations in parasympathetic
and/or sympathetic tone at the level of the atrioventricular node, superimposed on the effectively random sequence of impulses reaching the distal node due to
concealed penetration of multiple wave fronts (13)
engaging the perinodal atrium from different directions
(11, 24). It should be noted that the R-R interval power
spectra did not reveal narrow peaks within ranges
characteristic of parasympathetic or sympathetic oscillations, but it is possible that this may represent an
intrinsic limitation of Fourier analysis in such a ‘‘noisy’’
system. The two patients with the highest degrees of
predictability had coarse atrial fibrillation on the surface ECG, but the physiological significance of this
observation is uncertain.
Limitations. It is possible that analysis of longer
recordings would have yielded better predictability
because, for a short time series, ‘‘nearest’’ neighbors in
phase space are not necessarily ‘‘near’’ neighbors. We
chose a recording length of ⬃2,000 intervals to maximize stationarity of the underlying system. Likewise, it
is possible that analysis of embedding dimensions ⬎10
would have yielded better predictability. However, there
was no evidence suggesting this, and the results would
not, in any event, reflect low-dimensional chaos. Similarly, using the three nearest neighbors for prediction
was an empirical choice; others have proposed using
the single nearest neighbor for prediction (16). However, although this may have had some quantitative
effect, it is unlikely that it would qualitatively affect our
results. Finally, to study patients with stable chronic
atrial fibrillation, it was necessary to accept patients
undergoing treatment with a variety of medications
including digoxin, ␤-blockers, calcium-channel blockers, and antiarrhythmic drugs. Although we observed
no important differences accorded to the use of any of
these agents, the possibility that subtle drug effects
may have altered the results cannot be fully excluded.
In summary, despite the above considerations, the
present data demonstrate the potential of nonlinear
predictive forecasting as a tool for qualitative analysis
of dynamic systems and demonstrate that atrial fibrillation is not a chaotic rhythm. Furthermore, although
the pathophysiological significance is not clear, the
technique reveals the existence of a subset of patients
with atrial fibrillation whose R-R interval sequence is
not entirely unpredictable.
H457
H458
VENTRICULAR RESPONSE IN ATRIAL FIBRILLATION
23. Stein, K. M., and P. Kligfield. Fractal clustering of ventricular
ectopy in dilated cardiomyopathy. Am. J. Cardiol. 65: 1512–
1515, 1990.
24. Stein, K. M., and B. B. Lerman. Evidence for functionally
distinct dual atrial inputs to the human AV node. Am. J. Physiol.
267 (Heart Circ. Physiol. 36): H2333–H2341, 1994.
25. Sugihara, G., and R. M. May. Nonlinear forecasting as a way of
distinguishing chaos from measurement error in time series.
Nature 344: 734–741, 1990.
26. Takens, F. Detecting strange attractors in turbulence. Lect.
Notes Math. 898: 366–381, 1980.
27. Tsonis, A. A., and J. B. Elsner. Nonlinear prediction as a way of
distinguishing chaos from random fractal sequences. Nature 358:
217–220, 1992.
28. Van den Berg, M. P., J. Haaksma, J. Brouwer, R. G.
Tieleman, G. Mulder, and H. J. G. M. Crijns. Heart rate
variability in patients with atrial fibrillation is related to vagal
tone. Circulation 96: 1209–1216, 1997.
29. Wittkampf, F. H. M., M. J. L. de Jongste, H. I. Lie, and F. L.
Meijler. Effect of right ventricular pacing on ventricular rhythm
during atrial fibrillation. J. Am. Coll. Cardiol. 11: 539–545,
1988.
Downloaded from http://ajpheart.physiology.org/ by 10.220.33.3 on May 6, 2017