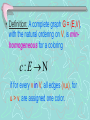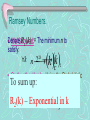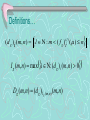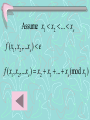* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ramsey Theory
Functional decomposition wikipedia , lookup
Mathematical proof wikipedia , lookup
Big O notation wikipedia , lookup
Computability theory wikipedia , lookup
Fundamental theorem of calculus wikipedia , lookup
Dirac delta function wikipedia , lookup
Principia Mathematica wikipedia , lookup
Elementary mathematics wikipedia , lookup
Function (mathematics) wikipedia , lookup
History of the function concept wikipedia , lookup
Non-standard calculus wikipedia , lookup
Thresholds for Ackermannian
Ramsey Numbers
Authors:
Menachem Kojman
Gyesik Lee
Eran Omri
Andreas Weiermann
Notation…
• n = {1..n}
•
n
k c
2
means:
for every coloring C of the edges of the complete graph Kn,
there is a complete Q monochromatic sub-graph of size k.
n – Size of complete graph over which we color edges.
k – Size of homogeneous sub-graph.
c – Number of colors.
2 – Size of tuples we color – pairs (edges).
Q is homogeneous for C
Example
Example…
Let us prove:
•22 k 1
k 2 means:
for every coloring C of the edges of the complete graph Kn,
there is a complete Q monochromatic sub-graph of size k.
n = 22k-1 – Size of complete graph over which we color edges.
k – Size of homogeneous sub-graph.
c = 2 – Number of colors.
Proof…
• Let us, from now on, assume the vertex
set of every graph we consider is some
initial segment of the natural numbers.
• First step:
Find a min-homogeneous complete
sub-graph of size 2k.
• Definition: A complete graph G = (E,V),
with the natural ordering on V, is minhomogeneous for a coloring
c:E
if for every v in V, all edges (v,u), for
u > v, are assigned one color.
…Proof…
Let G = (V,E) be the complete graph with
V= 22k-1:
x1 x2 x3 x4 x5 x6 …
… x2
And let C be a coloring of the vertices
of G with 2 colors (Red, Blue).
C(x1,x2) = red
C(x2,x6) = blue
2k-1
…Proof…
Mark xi with the color C(x1, xi)
x1 x2 x3 x4 x5 x6
…
There is a monochromatic complete
sub-graph of {x2,x3,…} of size 22k-2.
(Say red)
… x2
2k-1
…Proof…
Mark xi with the color C(x2, xi)
x1 x2 x3
x6
…
There is a monochromatic complete
sub-graph of {x3,x6,…} of size 22k-3.
(Say blue)
…Proof…
Now, we have a min-homogeneous
sequence {xi , xi , xi , …, xi }
1
xi
1
xi
xi
2
2
3
3
xi
2k
xi
4
5
xi …
6
xi
2k
Mark
x
with
C(x
,
x
)
for
all
b
>
a.
i
i
i
•Second (and final) step:
a
a
b
Find
homogeneous complete
There
isaak-sized
monochromatic
subsetsub-graph
of
{xi , xi , xi , … xi } of size k.
1
2
3
2k
Ramsey Numbers.
Rc(k) := The minimum n to
•Denote
We Showed:
satisfy:
ck
k n
2
k
2k
2
• On the other Hand: - Using the Probabilistic
To
sum
up:
Method, we can show:
R2(k) – Exponential
in kk
k 2
2
k
2
2
• More importantly:
k , c
c
k
min
k
c
• Explanation: - For a k-sized sequence iterate
step #1 (repeated division) k times (namely,
divide by at most c at each iteration)
Primitive Recursive Functions
and Ackermann’s Function
A function that can be implemented
using only for-loops is called
primitive recursive.
Ackermann’s function – A simple example
of a well defined total function that is
computable but not primitive recursive
Regressive Ramsey….
• g-regressive colorings:
A coloring C is g-regressive if for every (m,n)
C(m,n) ≤ g(min(m,n)) = g(m)
• Can we still demand homogeneity??
• Not necessarily!!! ( e.g C(m,n) = Id(m) )
Observe that
Is true for any g: N N which can be
k
n
n k
g
established by means, similar to the
regular Ramsey proof and compactness.
min
The g-regressive Ramsey Number
Denote Rg(k) := The minimum n to
satisfy:
n
min
k g
We have seen so far:
For a constant function, g(x) = c
Rg(k) ≤ ck Since c
k
min
k g
On the other hand it was known…
That for g = ID:
Rg(k) is Ackermannian in terms of k.
Namely, DOMINATES every primitive
recursive function.
The Problem
• constant g
Rg(k) < gk (primitive recursive.)
• Threshold g
Rg(k) is ackermannian.
• g = Id
g(x)
The Results
1/k
IfIfg(n)
is
‘fast’
to
go
below
n
1/j - Ackermannian
g(n) ≤ n1/kxthen,
then, Rg(k) is primitive recursive
mininsert a drawing
k will
I
n ( g (n)) k
g
x
The Results
Suppose B : N N is positive, unbounded
and non-decreasing.
1/B−1(n)
Let gB(n) = n
. Where
B-1(n) = min{t : B(t) ≥ n}. Then,
Rg (k) is Ackermannian
B
iff
B is Ackermannian.
Min-homogeneity – Lower Threshold
Basic Pointers:
Suppose B : N N is positive, unbounded
•andAssume
more
colors.
non-decreasing.
Set c =1/gBB−1(n)
(n)
Let gB(n) = n
. Where
• Use
repeated
division
show
B-1(n)
= min{t
: B(t)
≥ n}.toThen,
B(k) ≥
ck
min
(k)g
for every natural number
k, it holds that
B
Rg (k) ≤ B(k).
B
Min-homogeneity – Upper Threshold
• We show:
1
j
if g(x) x for some j
then, Rg (k ) is Ackermanni an.
• To prove this, we present, given k,
a bad coloring of an Akermannianly large n
The=Bad
Coloring
C(m,n)
<I,D>
I k Largest i s.t m,n are not in same segment.
(fg)i(µ)
D Distance between m’s segment and
n’s.
(2)
(fg)3 (µ)
i
(fg)3(µ)
3
2
1
( f g )k ( )
µ µ+1 µ+2 …
{(fg)i}
The=Bad
Coloring
C(m,n)
<I,D>
= <2,1>
I
Largest
i
s.t
m,n
are
not
in
same
segment.
k
D Distance between m’s segment and n’s.
i
3
2
1
µ µ+1 µ+2 …
m = µ+8
n = µ+29
The Coloring – Formal Definition
Given a monotonically increasing function 4g2 and
a natural number k >2 with
min({ t : k g (t )})
we define a coloring c : []2
That is:
1. 4g2-regressive on the interval { , ( f g ) k ( ))
2. Has no min-homogeneous set of size k+1
within that interval.
Definitions…
(d g )i (m, n)
l : m ( f
g
I g (m, n) max i : (d g )i (m, n) 0
Dg (m, n) (d g ) I g ( m,n) (m, n)
)i ( ) n
(l )
The Coloring…
C g (m, n) pr( Dg (m, n), I g (m, n))
a b 1
So, why is it:
2
b 4(max( a, b))
pr( a, b)
2
2
4g -regressive?
Avoiding a min-homogeneous set?
The Results - Surfing the
waves
g(x)
x1/j - Ackermannian
I will insert a drawing
x
Besides The Asymptotic bounds,
We can also establish:
RId (82) A53 (2
2
274
)
[email protected]
In 1985 Kanamori & McAloon
Had used means of Model Theory to show that the
bound of :
k
n
n
min
k
2
ID
eventually DOMINATES every primitive recursive
function.
In 1991 Prömel, Thumser & Voigt and independently
in 1999 Kojman & Shelah have presented two
simple combinatorial proofs to this fact.
Primitive Recursive Functions
Input: Tuples of natural numbers
Output: A natural number
Basic primitive recursive functions:
• The constant function 0
• The successor function S
• The projection functions Pin(x1, x2,…, xn) = xi
Primitive Recursive Functions
More complex primitive recursive
functions are obtained by :
• Composition: h(x0,...,xl-1) =
f(g0(x0,...,xl-1),...,gk-1(x0,...,xl-1))
• Primitive recursion:
h(0,x0,...,xk-1) = f(x0,...,xk-1)
h(S(n),x0,...,xk-1) =
g(h(n,x0,...,xk-1),n,x0,...,xk-1)
General Definition – (fg) Hierarchy
Given a function g : N N,
denote
( f g )1 (n) n 1
( f g )i 1 (n) ( f g )
Where
0
f (n)
= n and
j+1
f (n)
( g ( n ))
i
=
( n)
j
f(f (n))
Ackermann’s Function
Let g = Id. Now
A1 (n) ( f g )1 (n) n 1
Ai1 (n) ( f g )i1 (n) A (n)
i
( n)
Denote: Ack(n) = An(n)
Ackermann’s Function
Examples:
A1 (n) n 1
A2 (n) A1 (n) 2n
( n)
A3 (n) A2 (n) 2
( n)
A4 (n) 2
22
..2n
22
n
3.
Infinite Canonical Ramsey theorem
(Erdös & Rado – 1950)
Definition…
e
canonical
e
Examples…
4. Finite Canonical Ramsey theorem
(Erdös & Rado – 1950)
k , e
n
n
canonical
k
e
e
H X is canonical for f : [ X ]
if I e so that
e
s, t [ H ] f ( s) f (t ) s | I t | I
Assume x1 x2 ... xe
f ( x1 , x2 ,...xe ) e
f ( x1 , x2 ,...xe ) x2 x3 ... xe (mod x1 )
1. clearly:
I g (m, n) k g (m)
2. On the other hand there exist t,l such that:
t ( f g )i(l )1 ( ) m n ( f g )i(l 11) ( ) ( f g )i 1 (t )
Now, since
We have
( f g )i 1 (t ) ( f g )i( g (t ) ) (t )
g (t ) (d g )i (t , ( f g )i 1 (t )) Dg (m, n)
And thus:
pr( I g (m, n), Dg (m, n)) 4( g (m))
2
The Bad Coloring
k
i
3
2
1
µ µ+1 µ+2 …
There exists no:
x0 x1 ... xi with
(d g ) ( x0 , xi ) 0
i
Which is min-homogeneous for Cg...
But, for every (m,n) in the interval,
(d g ) (m, n) 0
k
Homogeneity – Lower Bound
• We show:
for some f : s.t lim f (n)
n
lg x
if g(x)
lg lg x f ( x)
then, k n n
(k ) 2
g
• To prove that we used:
c
ck
k
2
c
Homogeneity – Upper Bound
• We showed:
lg x
if g(x)
for some s
s
then, k n n
(k ) 2
g
To do that we used a general, well known, coloring
method…
The s-basis coloring
Example…
The rules:
Imagine yourself in a
1. Any
two players
may choose to play Pool or
billiard
hall…
Snooker. (Coloring pairs with two colors)
A tournament
being
2. A tournament
can takeisplace
either in
Snooker
or in Pool. All the couples must
organized…
choose the same. (Homogeneous set)
3. Three players minimum. (Size of subset)
How many players will ensure
a Tournament??
6
Ramsey Number for 3 is 6.
Pool
=
Snooker =
General Definition – (fg) Hierarchy
Given a function g : N N,
denote
( f g )1 (n) n 1
( f g )i 1 (n) ( f g )
Where
0
f (n)
= n and
j+1
f (n)
( g ( n ))
i
=
( n)
j
f(f (n))
Suppose g : N N is nondecreasing and
unbounded. Then,
Rg(k) is bounded by some primitive recursive
function in k
iff
for every t > 0 there is some M(t) s.t for all n
≥ M(t) it holds that g(n) < n1/t and M(t) is
primitive recursive in t.